

2025年高考数学精品教案第八章 平面解析几何 第1讲 直线的方程
展开学生用书P169
1.直线的倾斜角与斜率
2.直线方程的五种形式
注意 (1)当直线与x轴不垂直时,可设直线方程为y=kx+b;当直线与y轴不垂直时,可设直线方程为x=my+n.
(2)截距是指直线与坐标轴交点的坐标值,可正,可负,可零.
1.下列说法正确的是( D )
A.直线的倾斜角越大,其斜率越大
B.若直线的斜率为tan α,则其倾斜角为α
C.经过定点P(x0,y0)的直线都可以用方程y-y0=k(x-x0)表示
D.截距可以为负值
解析 对于A,倾斜角为钝角的直线的斜率为负值,故A错误;对于B,一条直线的斜率为tan α,此直线的倾斜角不一定为α,如直线y=x的斜率为tan 5π4,它的倾斜角为π4,B错误;对于C,当经过定点P(x0,y0)的直线与x轴垂直时,斜率不存在,故C错误;对于D,截距可以取正数、负数或零,所以D正确.
2.[易错题]已知直线l:xtan 60°+y-3=0,则直线l的倾斜角α为( C )
A.30°B.60°C.120°D.150°
解析 ∵xtan 60°+y-3=0,∴y=-xtan 60°+3=xtan 120°+3,故直线l的倾斜角是120°,故选C.
3.倾斜角为135°,在y轴上的截距为-1的直线方程是( D )
A.x-y+1=0B.x-y-1=0C.x+y-1=0D.x+y+1=0
解析 ∵直线倾斜角是135°,∴直线的斜率等于-1,∵在y轴上的截距是-1,由直线方程的斜截式得:y=-1×x-1,即x+y+1=0,故选D.
4.[多选]如图,直线l1,l2,l3的斜率分别为k1,k2,k3,倾斜角分别为α1,α2,α3,则下列选项正确的是( AD )
A.k1<k3<k2B.k3<k2<k1
C.α1<α3<α2D.α3<α2<α1
解析 由题图知,k2>k3>0,k1<0,故π2>α2>α3>0,且α1为钝角,故选AD.
5.[教材改编]经过A(0,3),B(-2,0)两点的直线的方向向量为(1,k),则k的值为 32 .
解析 由题意可得k=32.
6.[易错题]已知点A(3,4),则经过点A且在两坐标轴上截距相等的直线方程为 4x-3y=0或x+y-7=0 .
解析 设直线在x轴、y轴上的截距均为a.(讨论截距是否为0)
①若a=0,即直线过点(0,0)及(3,4),
则直线的方程为y=43x,即4x-3y=0;
②若a≠0,设所求直线的方程为xa+ya=1,
又点(3,4)在直线上,所以3a+4a=1,所以a=7.
所以直线的方程为x+y-7=0.
综上可知,所求直线的方程为4x-3y=0或x+y-7=0.
学生用书P170
命题点1 直线的倾斜角与斜率
例1 (1)直线2xcs α-y-3=0(α∈[π6,π3])的倾斜角的取值范围是( B )
A.[π6,π3]B.[π4,π3]C.[π4,π2]D.[π4,2π3]
解析 直线2xcs α-y-3=0的斜率k=2cs α,因为α∈[π6,π3],所以12≤cs α≤32,因此k=2cs α∈[1,3].设直线的倾斜角为θ,则有tan θ∈[1,3].又θ∈[0,π),所以θ∈[π4,π3],即倾斜角的取值范围是[π4,π3].故选B.
(2)[2022新高考卷Ⅱ]图1是中国古代建筑中的举架结构,AA',BB',CC',DD'是桁,相邻桁的水平距离称为步,垂直距离称为举.图2是某古代建筑屋顶截面的示意图,其中DD1,CC1,BB1,AA1是举,OD1,DC1,CB1,BA1是相等的步,相邻桁的举步之比分别为DD1OD1=0.5,CC1DC1=k1,BB1CB1=k2,AA1BA1=k3.已知k1,k2,k3成公差为0.1的等差数列,且直线OA的斜率为0.725,则k3=( D )
图1图2
B.0.8D.0.9
解析 如图,连接OA,延长AA1与x轴交于点A2,则OA2=4OD1.因为k1,k2,k3成公差为0.1的等差数列,所以k1=k3-0.2,k2=k3-0.1,所以tan∠AOA2=AA2OA2=0.5OD1+k1DC1+k2CB1+k3BA14OD1=0.5+k1+k2+k34=0.5+k3-0.2+k3-0.1+k34=0.725,解得k3=0.9,故选D.
方法技巧
1.直线斜率的求解方法
(1)定义法:k=tan α(α为直线的倾斜角,且α≠π2);(2)公式法:k=y2-y1x2-x1 ((x1,y1),(x2,y2)为直线上两点,且x1≠x2).
2.直线斜率与倾斜角之间的关系往往借助正切函数在[0,π)上的图象判断,注意正切函数在[0,π)上不单调,要注意分类讨论.
训练1 (1)已知点A(-1,1),B(1,2),C(0,-1),过点C的直线l与线段AB有公共点,则直线l的斜率k的取值范围是( C )
A. [-2,3]B. [-2,0)∪(0,3]
C. (-∞,-2]∪[3,+∞)D.以上都不对
解析 如图所示,∵过点C的直线l与线段AB有公共点,∴直线l的斜率k≥kBC或k≤kAC,又kBC=2-(-1)1-0=3,kAC=1-(-1)-1-0=-2,∴k≥3或k≤-2,∴直线l的斜率k的取值范围是(-∞,-2]∪[3,+∞),故选C.
(2)直线x+(a2+1)y+1=0的倾斜角的取值范围是( B )
A.[0,π4]B.[3π4,π)
C.[0,π4]∪(π2,π]D.[π4,π2)∪[3π4,π)
解析 因为a2+1≠0,所以直线的斜率k=-1a2+1,设直线的倾斜角为α,则tanα=-1a2+1,所以-1≤tan α<0,所以3π4≤α<π,故选B.
命题点2 求直线的方程
例2 (1)已知点M是直线l:2x-y-4=0与x轴的交点,将直线l绕点M按逆时针方向旋转45°,得到的直线方程是( D )
A.x+y-3=0B.x-3y-2=0
C.3x-y+6=0D.3x+y-6=0
解析 设直线l的倾斜角为α,则tan α=k=2,
直线l绕点M按逆时针方向旋转45°,所得直线的斜率k'=tan(α+π4)=2+11-2×1=-3,又由题意得点M(2,0),
所以所求直线方程为y=-3(x-2),即3x+y-6=0,故选D.
(2)已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,当△ABO的面积最小时,直线l的方程为 2x+3y-12=0 .
解析 解法一 设A(a,0),B(0,b)(a>0,b>0),则直线l的方程为xa+yb=1.因为l过点P(3,2),所以3a+2b=1.因为1=3a+2b≥26ab,整理得ab≥24,所以S△ABO=12ab≥12,当且仅当3a=2b,即a=6,b=4时取等号.此时直线l的方程是x6+y4=1,即2x+3y-12=0.
解法二 依题意知,直线l的斜率k存在且k<0,则直线l的方程为y-2=k(x-3),则A(3-2k,0),B(0,2-3k),
S△ABO=12(2-3k)(3-2k)=12[12+(-9k)+4-k]≥12[12+2(-9k)·4-k ]=12×12+12=12,
当且仅当-9k=4-k,即k=-23(正值舍去)时,等号成立.
所以所求直线l的方程为2x+3y-12=0.
方法技巧
求直线方程的两种方法
训练2 在平面直角坐标系中,O为坐标原点,已知点A(1,2),B(4,7),若点C满足OC=αOA+βOB(α,β∈R,且α+β=1),则点C的轨迹方程为 5x-3y+1=0 .
解析 ∵点C满足OC=αOA+βOB(α,β∈R,且α+β=1),∴OC=αOA+1-αOB=αOA-OB+OB,∴OC-OB=α(OA-OB),∴BC=αBA,由共线向量基本定理可知,A,B,C三点共线,∴点C的轨迹为直线AB,
又A(1,2),B(4,7),∴直线AB的方程为y-27-2=x-14-1,整理得5x-3y+1=0,故点C的轨迹方程为5x-3y+1=0.
命题点3 直线方程的综合应用
例3 (1)已知点A(2,5),B(4,1).若点P(x,y)在线段AB上,则2x-y的最大值为( C )
A.-1B.3C.7D.8
解析 依题意得kAB=5-12-4=-2,则线段lAB:y-1=-2(x-4),x∈[2,4],即y=-2x+9,x∈[2,4],故2x-y=2x-(-2x+9)=4x-9,x∈[2,4].设h(x)=4x-9,x∈[2,4],易知h(x)=4x-9在[2,4]上单调递增,故当x=4时,h(x)max =4×4-9=7.
(2)已知直线l的方程为(a+1)x+y+3-a=0(a∈R),则直线l过定点 (1,
-4) ;若直线l不经过第三象限,则实数a的取值范围是 [3,+∞) .
解析 直线l:(a+1)x+y+3-a=0可化为a(x-1)+x+y+3=0,令x-1=0,x+y+3=0,解得x=1,y=-4,∴直线l过定点(1,-4).∵直线l的方程可化为y=-a+1x+a-3,且直线l不经过第三象限,∴-(a+1)<0,a-3≥0,解得a≥3.
方法技巧
1.与直线有关的范围问题要注意借助函数或者不等式求解.
2.直线方程含参数时,注意判断直线是否过定点或者斜率是否为定值.
训练3 (1)[2024广东深圳模拟]在平面直角坐标系xOy中,已知动点P(a,b)到两直线l1:y=2x与l2:y=-12x+1的距离之和为5,则ba+5的取值范围是 [-311,917] .
解析 直线l1:y=2x与l2:y=-12x+1的方程化为一般式分别为l1:2x-y=0,l2:x+2y-2=0,所以点P(a,b)到两直线的距离之和为|2a-b|5+|a+2b-2|5=5,即2a-b+a+2b-2=5 ①.
当2a-b≥0,a+2b-2≥0时,①式变形为3a+b=7;当2a-b≥0,a+2b-2<0时,①式变形为a-3b=3;当2a-b<0,a+2b-2≥0时,①式变形为-a+3b=7;当2a-b<0,a+2b-2<0时,①式变形为-3a-b=3.则动点P(a,b)的轨迹为如图所示的正方形ABCD,ba+5的几何意义为正方形边上任意一点与E(-5,0)连线的斜率.计算得C(-35,-65),D(-85,95),kCE=-311,kDE=917,所以ba+5的取值范围是[-311,917].
(2)[2023长春模拟]已知直线l1:x-my+1=0过定点A,直线l2:mx+y-m+3=0过定点B,l1与l2相交于点P,则|PA|+|PB|的最大值为 26 .
解析 直线l1:x-my+1=0过定点A(-1,0);直线l2的方程可化为mx-1+y+3=0,令x=1,得y=-3,所以直线l2过定点B(1,-3).因为1·m-m·1=0,所以l1⊥l2.
因为l1与l2相交于点P,所以|PA|2+|PB|2=|AB|2=(-1-1)2+(0+3)2=13.
因为|PA|2+|PB|22≥(|PA|+|PB|2)2,所以|PA|+|PB|≤26,当且仅当PA=PB=262时等号成立.
1.[命题点1/与函数综合]函数f(x)=csx2+sinx的值域为 [-33,33] .
解析 csx2+sinx可看作点A(2,0)和点B(-sin x,-cs x)连线的斜率,易得点B在圆O:x2+y2=1上,作出图象如图所示.设过点A的直线分别与圆O相切于点C,D,连接OC,OD,则由OD=OC=1=OA=2易得∠OAD=∠OAC=30°,所以kAC=33,kAD=-33,所以函数f(x)的值域为[-33,33].
2.[命题点2]过点(-3,4),且在两坐标轴上的截距之和为12的直线方程为 4x-y+16=0或x+3y-9=0 .
解析 由题设知,直线在x轴、y轴上的截距均不为0,设直线方程为xa+y12-a=1,
又直线过点(-3,4),从而-3a+412-a=1,解得a=-4或a=9,故直线方程为4x-y+16=0或x+3y-9=0.
3.[命题点2]已知两条不重合的直线l1:a1x+b1y+1=0和l2:a2x+b2y+1=0都过点A(2,1),则过点P1(a1,b1)和点P2(a2,b2)的直线方程是( A )
A.2x+y+1=0B.2x-y+1=0
C.2x+y-1=0D.x+2y+1=0
解析 把A(2,1)代入直线l1和l2的方程,得2a1+b1+1=0,2a2+b2+1=0,则2(a1-a2)=b2-b1.又过点P1(a1,b1),P2(a2,b2)的直线的方程是y-b1b2-b1=x-a1a2-a1,∴y-b1=-2(x-a1),即2x+y-(2a1+b1)=0,∵2a1+b1+1=0,∴2a1+b1=-1,∴所求直线方程为2x+y+1=0.故选A.
4.[命题点2,3/2024四川内江模拟]已知直线l:(m+1)x+(m-3)y+2m+10=0(m∈R).
(1)求证:直线l与直线3x+7y-2=0总相交.
(2)若直线l交x轴的负半轴于点A,交y轴的正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
解析 (1)直线l可变形为m(x+y+2)+x-3y+10=0,令x+y+2=0,x-3y+10=0,解得x=-4,y=2,
故直线l恒过点(-4,2),
又3×(-4)+7×2-2=0,
故点(-4,2)在直线3x+7y-2=0上,
故直线l与直线3x+7y-2=0总相交.
(2)若直线l交x轴的负半轴于点A,交y轴的正半轴于点B,则直线l的斜率存在且大于0,
故-m+1m-3>0,解得-1<m<3.
在(m+1)x+(m-3)y+2m+10=0(m∈R)中,
令y=0,得x=-2m+10m+1;
令x=0,得y=-2m+10m-3.
则S=12×2m+10m+1×(-2m+10m-3)=-2(m+5)2(m+1)(m-3),令m+5=t∈(4,8),则S=-2t2(t-4)(t-8)=-2t2t2-12t+32=-232t2-12t+1=-232(1t-316)2-18,
因为1t∈(18,14),
所以当1t=316时,S取得最小值,最小值为16,
此时m+5=163,m=13,直线l的方程为x-2y+8=0.
学生用书·练习帮P348
1.[2024江苏南京联考]过两点A(3,y),B(2,0)的直线的倾斜角为120°,则y=( D )
A.33B.3C.-33D.-3
解析 设直线斜率为k,则k=tan 120°=y-03-2=y=-3,故选D.
2.已知点A(-2,3)和B(4,2),若直线l:x+my+m-1=0与线段AB有交点,则实数m的取值范围是( C )
A.(-∞,-1)∪(34,+∞)
B.(-1,34)
C.[-1,34]
D.(-∞,-1)∪[34,+∞)
解析 如图,直线l:x+my+m-1=0恒过定点P(1,-1),kAP=-43, kBP=1.当m=0时,直线l的方程为x=1,与线段AB有交点,符合题意;当m≠0时,直线l的斜率为-1m,则-1m≥1或-1m≤-43,解得-1≤m<0或0<m≤34.综上,m∈[-1,34],故选C.
3.[2024四川成都七中段考]若直线l的方程为6x-6ycs β+13=0,则直线l的倾斜角α的取值范围是( D )
A.[0,π]B.[π4,π2]
C.[π4,π2)∪(π2,3π4)D.[π4,3π4]
解析 当cs β=0时,l的方程为6x+13=0,直线l的倾斜角α=π2;当cs β≠0时,由直线方程可得斜率k=1csβ=tan α,∵cs β∈[-1,1],且cs β≠0,∴tan α∈(-∞,-1]∪[1,+∞),又α∈[0,π),∴α∈[π4,π2)∪(π2,3π4].综上,倾斜角α的取值范围是[π4,3π4].故选D.
4.[2024贵州联考]若直线l:(a-2)x+ay+2a-3=0经过第四象限,则实数a的取值范围为( C )
A.(-∞,0)∪(2,+∞)B.(-∞,0)∪[2,+∞)
C.(-∞,0)∪(32,+∞)D.(-∞,0)∪[32,+∞)
解析 若a=0,则l的方程为x=-32,不经过第四象限.若a=2,则l的方程为y=-12,经过第四象限.若a≠0且a≠2,将l的方程转化为y=-a-2ax-2a-3a,因为l经过第四象限,所以-a-2a<0或-a-2a>0,-2a-3a<0,解得a<0或32<a<2或a>2.综上,a的取值范围为(-∞,0)∪(32,+∞),故选C.
5.[2023山西模拟]将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(2,0),C(0,1),将矩形纸片折叠,使点O落在线段BC上,设折痕所在直线的斜率为k,则k的取值范围是( D )
A.[0,1]B.[0,2]C.[-1,0)D.[-2,0]
解析 要想折叠后使点O落在线段BC上,可取BC上任意一点D,作线段OD的垂直平分线l,以l为折痕可使点O与点D重合,如图.因为kOD≥kOB=12,且k=-1kOD,所以-2≤k<0.
又当折叠后点O与点C重合时,k=0,所以-2≤k≤0,
所以实数k的取值范围是[-2,0].
6.[2024广东佛山容山中学校考]已知直线l的斜率小于0,且l经过点P(6,8),并与坐标轴分别交于A,B两点,C(4,0),当△ABC的面积取得最小值时,直线l的斜率为( C )
A.-33B.-354C.-433D.-324
解析 由题意可设直线l:y=kx+b(k<0),将点P的坐标代入,得8=6k+b,则b=8-6k,则y=kx+8-6k(k<0).不妨设A在x轴上,则A(6-8k,0),B(0,8-6k).
记O为坐标原点,因为线段OA与OB的长度分别为6-8k,8-6k,所以△ABC的面积S=12(6-8k-4)(8-6k)=12(64-64k-12k)≥12×(64+2×64×12)=32+163,当且仅当-64k=-12k(k<0),即k=-433时等号成立.故选C.
7.[多选/2024黑龙江牡丹江段考]已知直线l过点P(4,5),且直线l在两坐标轴上的截距的绝对值相等,则直线l的方程可能为( ABC )
A.5x-4y=0B.x-y+1=0
C.x+y-9=0D.x+y+1=0
解析 当直线l过原点时,设直线方程为y=kx,又直线过点P(4,5),则直线l的方程为y=54x,即5x-4y=0,故A正确;
当直线l不过原点,且在两坐标轴上的截距相等时,设直线方程为xa+ya=1,又直线过点P(4,5),则9a=1,得a=9,则直线l的方程为x+y-9=0,故C正确;
当直线l不过原点,且在两坐标轴上的截距互为相反数时,设直线方程为xb-yb=1,又直线过点P(4,5),则-1b=1,得b=-1,则直线l的方程为x-y+1=0,故B正确.故选ABC.
8.[多选]已知直线l:(t+2)x+(t-1)y+3=0,则下列结论正确的是( ACD )
A.直线l的斜率可以等于0
B.直线l的斜率一定存在
C.当t=-12时,直线l的倾斜角为π4
D.点P(1,3)到直线l的最大距离为22
解析 对于A,当t=-2时,直线l的斜率为0,故A正确;对于B, 当t=1时,直线l的斜率不存在,故B错误;对于C,当t=-12时,直线l:32x-32y+3=0,即y=x+2,斜率为1,倾斜角为π4,故C正确;对于D,直线l:(t+2)x+(t-1)y+3=0,即2x-y+3+tx+y=0,恒过2x-y+3=0和x+y=0的交点M(-1,1),易知点P(1,3)到直线l的最大距离为|PM|=(1+1)2+(3-1)2=22,故D正确.
9.已知直线l的斜率为16,且与两坐标轴围成面积为3的三角形,则l的斜截式方程为 y=16x+1或y=16x-1 .
解析 设直线l的方程为y=16x+b,令x=0,得y=b,令y=0,得x=-6b,所以12|b|·|-6b|=3,即b2=1,所以b=±1.故所求直线方程为y=16x+1或y=16x-1.
10.已知点M(x,y)是函数y=-2x+8图象上的一点,则当x∈[2,5]时,y+1x+1的取值范围为 [-16,53] .
解析 y+1x+1=y-(-1)x-(-1)的几何意义是过M(x,y),N(-1,-1)两点的直线的斜率.设A(2,4),B(5,-2),因为点M在函数y=-2x+8的图象上,且x∈[2,5],所以点M在线段AB上.因为kNA=53,kNB=-16,所以-16≤y+1x+1≤53.
11.若直线l与曲线y=x和圆x2+y2=15都相切,则l的方程为( D )
A.y=2x+1B.y=2x+12
C.y=12x+1D.y=12x+12
解析 易知直线l的斜率存在,设直线l的方程为y=kx+b,则|b|k2+1=55 ①,设直线l与曲线y=x的切点坐标为(x0,x0)(x0>0),则y'|x=x0=12x0-12=k ②,x0=kx0+b ③,由②③可得b=12x0,将b=12x0,k=12x0-12代入①得x0=1或 x0=-15(舍去),所以k=b=12,故直线l的方程为y=12x+12.
12.[多选/2024江西宜春丰城中学月考]已知点A(-2,-1),B(2,2),直线l:2ax-2y+3a-3=0上存在点P满足|PA|+|PB|=5,则直线l的倾斜角可能为( BD )
A.0B.π4C.π2D.3π4
解析 将点A(-2,-1)代入直线l:2ax-2y+3a-3=0得a=-1,再将点B(2,2)代入直线l:2ax-2y+3a-3=0得a=1,∴点A,B不可能同时在直线l上,又|AB|=(-2-2)2+(-1-2)2=5,且PA+PB=5,∴点P的轨迹为线段AB,即直线l与线段AB恒有交点.又直线l:2ax-2y+3a-3=a(2x+3)+(-2y-3)=0,∴直线l恒过定点C(-32,-32),作出示意图如图所示,此时kAC=-1+32-2+32=-1,kBC=2+322+32=1,故直线l的斜率的取值范围为(-∞,-1]∪[1,+∞),且直线l的斜率存在,故直线l的倾斜角的取值范围为[π4,π2)∪(π2,3π4],故选BD.
13.[情境创新]1949年公布的《国旗制法说明》中就五星的位置规定:大五角星有一个角尖正向上方,四颗小五角星均各有一个角尖正对大五角星的中心点.有人发现,第三颗小星的姿态与大星相近.为便于研究,如图,以大星的中心点为原点,建立直角坐标系,OO1,OO2,OO3,OO4分别是大星中心点与四颗小星中心点的连线,α≈16°,则第三颗小星的一条边AB所在直线的倾斜角约为( C )
A.0°B.1°C.2°D.3°
解析 因为O,O3都为五角星的中心点,所以OO3平分第三颗小星的一个角,又五角星的每个内角均为36°,可知∠BAO3=18°.过A作x轴的平行线AE(E在点A右侧),则∠EAO3=α≈16°,所以直线AB的倾斜角约为18°-16°=2°,故选C.课标要求
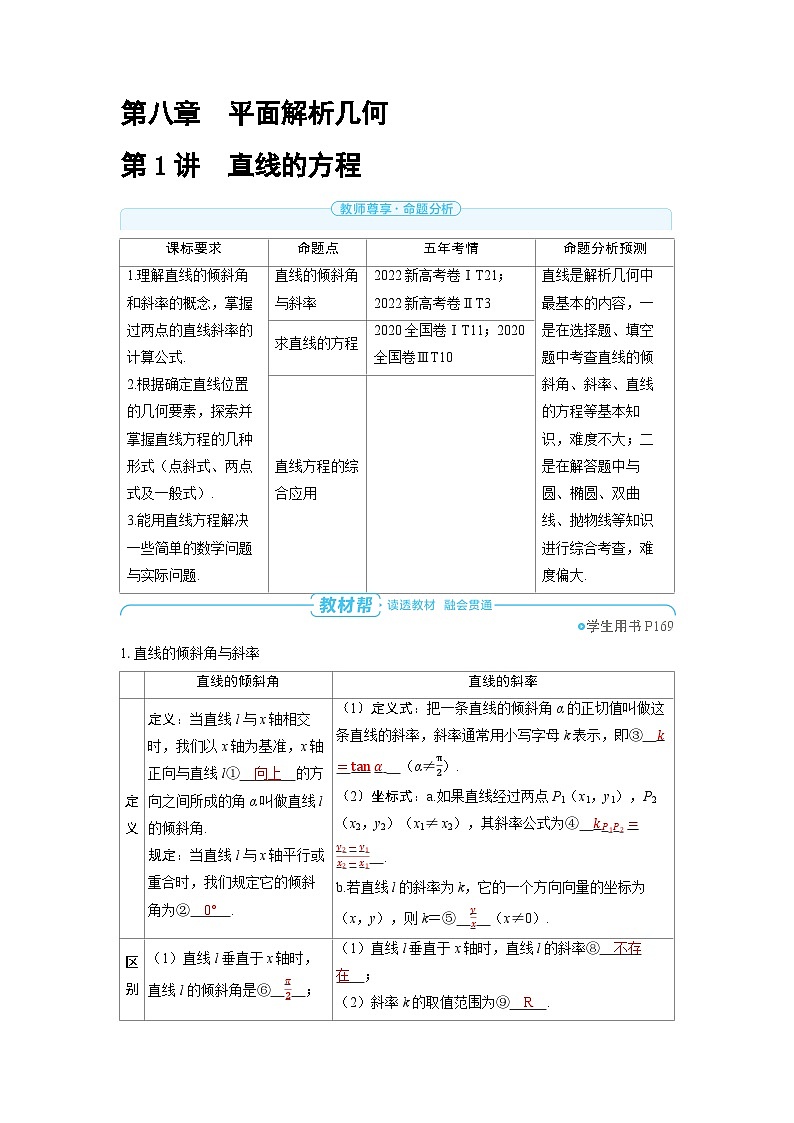
命题点
五年考情
命题分析预测
1.理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.
2.根据确定直线位置的几何要素,探索并掌握直线方程的几种形式(点斜式、两点式及一般式).
3.能用直线方程解决一些简单的数学问题与实际问题.
直线的倾斜角与斜率
2022新高考卷ⅠT21;2022新高考卷ⅡT3
直线是解析几何中最基本的内容,一是在选择题、填空题中考查直线的倾斜角、斜率、直线的方程等基本知识,难度不大;二是在解答题中与圆、椭圆、双曲线、抛物线等知识进行综合考查,难度偏大.
求直线的方程
2020全国卷ⅠT11;2020全国卷ⅢT10
直线方程的综合应用
直线的倾斜角
直线的斜率
定义
定义:当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l① 向上 的方向之间所成的角 α叫做直线l的倾斜角.
规定:当直线l与x轴平行或重合时,我们规定它的倾斜角为② 0° .
(1)定义式:把一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率通常用小写字母k表示,即③ k=tanα (α≠π2).
(2)坐标式:a.如果直线经过两点P1(x1,y1),P2(x2,y2)(x1≠ x2),其斜率公式为④ kP1P2=y2-y1x2-x1 .
b.若直线l的斜率为k,它的一个方向向量的坐标为(x,y),则k=⑤ yx (x≠0).
区别
(1)直线l垂直于x轴时,直线l的倾斜角是⑥ π2 ;(2)倾斜角的取值范围为⑦ [0,π) .
(1)直线l垂直于x轴时,直线l的斜率⑧ 不存在 ;
(2)斜率k的取值范围为⑨ R .
联系
如图,当直线l的倾斜角α∈[0,π2)时,α越大,直线l的斜率k越⑩ 大 ;
当α∈(π2,π)时,α越大,直线l的斜率k越⑪ 大 .
名称
方程
说明
适用条件
斜截式
y=kx+b
k是直线的斜率;b是直线在y轴上的截距.
与x轴不垂直的直线.
点斜式
⑫ y-y0=k(x-x0)
点(x0,y0)是直线上的已知点;k是斜率.
两点式
y-y1y2-y1=x-x1x2-x1
(x1≠x2,y1≠y2)
点(x1,y1),(x2,y2)是直线上的两个已知点.
与两坐标轴均不垂直的直线.
截距式
⑬ xa+yb=1
a是直线在x轴上的截距;
b是直线在y轴上的截距.
不过原点且与两坐标轴均不垂直的直线.
一般式
Ax+By+C=0
(A2+B2≠0)
当A≠0,B=0时,-CA是直线的横截距;
当A≠0,B≠0时,-AB,-CA,-CB分别为直线的斜率、在x轴上的截距、在y轴上的截距.
所有直线.
直接法
根据已知条件,选择适当的直线方程形式,直接写出直线方程.
待定系数法
先设所求直线方程的恰当形式,再由题设条件列方程(组),求出待定系数.
2025年高考数学精品教案第八章 平面解析几何 第2讲 两条直线的位置关系: 这是一份2025年高考数学精品教案第八章 平面解析几何 第2讲 两条直线的位置关系,共13页。
2025年高考数学精品教案第八章 平面解析几何 第4讲 直线与圆、圆与圆的位置关系: 这是一份2025年高考数学精品教案第八章 平面解析几何 第4讲 直线与圆、圆与圆的位置关系,共20页。
2025年高考数学精品教案第八章 平面解析几何 第5讲 椭 圆: 这是一份2025年高考数学精品教案第八章 平面解析几何 第5讲 椭 圆,共20页。












