沪科版（2024）七年级上册（2024）1.5 有理数的乘除教课内容课件ppt

这是一份沪科版（2024）七年级上册（2024）1.5 有理数的乘除教课内容课件ppt，共26页。PPT课件主要包含了-2cm，-3分钟，为了区分方向与时间，min后，负数与0相乘得0，min前，有理数乘法法则，先确定积的符号，再确定积的绝对值，解1－140等内容，欢迎下载使用。

如图,一只蜗牛沿直线 l爬行，它现在的位置在l上的点Ｏ．
1.如果一只蜗牛向右爬行2cm记为+2cm，那么向左爬行2cm应该记为 .
2.如果3分钟以后记为+3分钟，那么3分钟以前应该记为 .
（1）如果蜗牛一直以每分2cm的速度向右爬行，3分后它在什么位置？（2）如果蜗牛一直以每分2cm的速度向左爬行，3分后它在什么位置？（3）如果蜗牛一直以每分2cm的速度向右爬行，3分前它在什么位置？（4）如果蜗牛一直以每分2cm的速度向左爬行，3分前它在什么位置？（ 5 ）原地不动或运动了零次，结果是什么？
规定：向左为负，向右为正．　　　现在前为负，现在后为正．
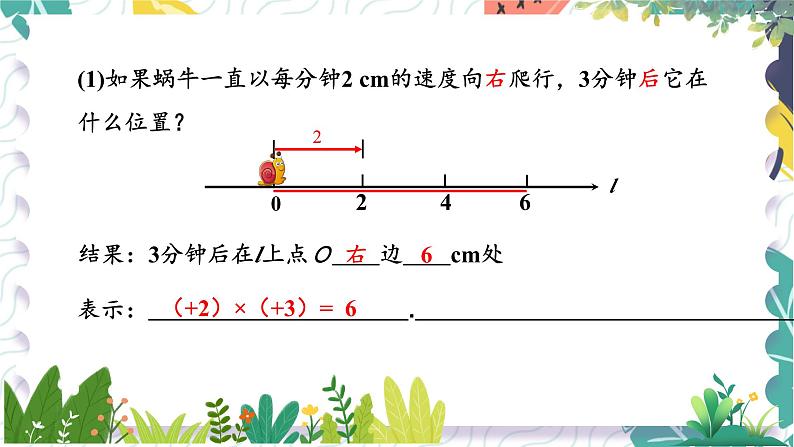
(1)如果蜗牛一直以每分钟2 cm的速度向右爬行，3分钟后它在什么位置？
结果：3分钟后在l上点Ｏ 边 cm处
表示： .
（+2）×（+3）= 6
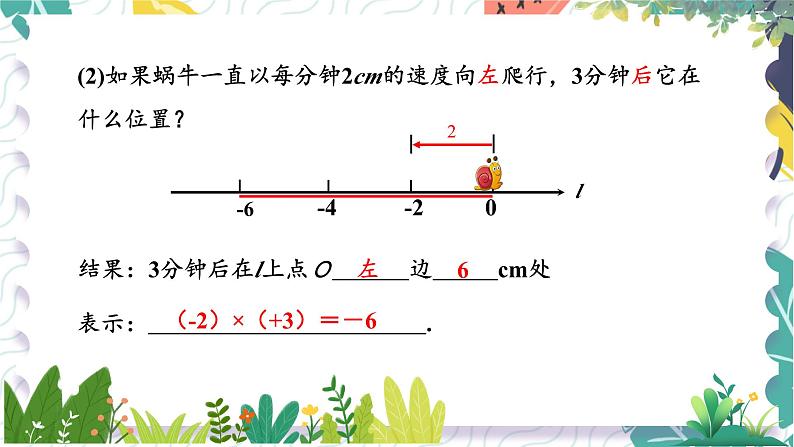
(2)如果蜗牛一直以每分钟2cm的速度向左爬行，3分钟后它在什么位置？
结果：3分钟后在l上点Ｏ 边 cm处
表示： .
（-2）×（+3）＝－6
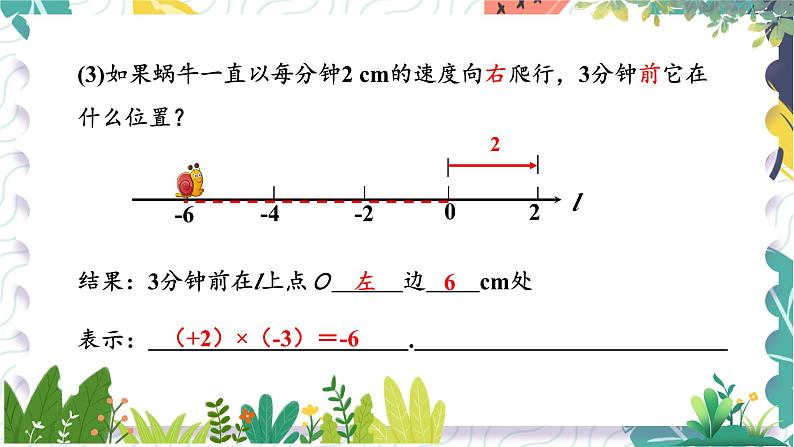
(3)如果蜗牛一直以每分钟2 cm的速度向右爬行，3分钟前它在什么位置？
结果：3分钟前在l上点Ｏ 边 cm处
表示： .
（+2）×（-3）＝-6
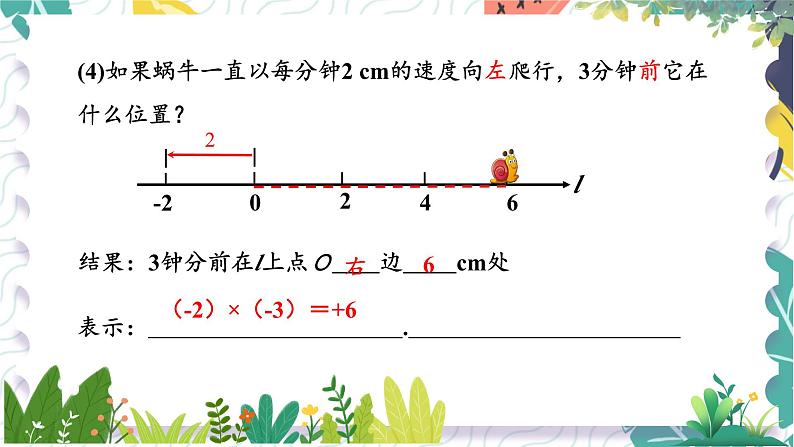
(4)如果蜗牛一直以每分钟2 cm的速度向左爬行，3分钟前它在什么位置？
结果：3钟分前在l上点Ｏ 边 cm处
表示： .
（-2）×（-3）＝+6　　　　　　　　
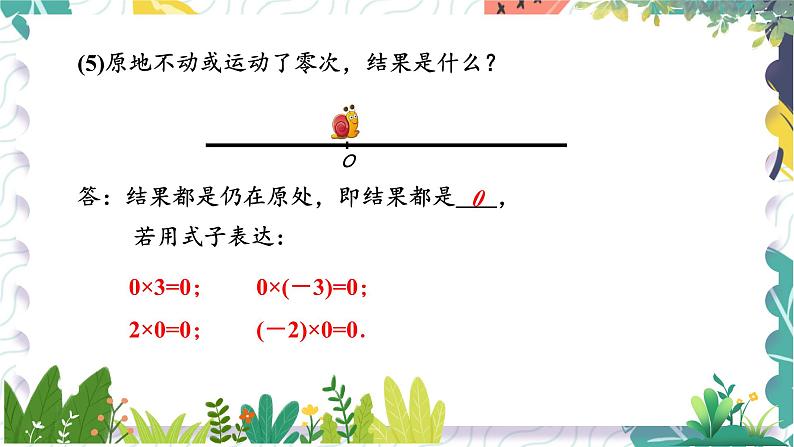
答：结果都是仍在原处，即结果都是 ， 若用式子表达：
(5)原地不动或运动了零次，结果是什么？
0×3=0； 0×(－3)=0；2×0=0； (－2)×0=0．
问题1 在实验室中，用冷却的方法可将某种生物标本的温度稳定地下降，每1 min下降2℃.假设现在生物标本的温度是0℃，问3 min后它的温度是多少？
用算式表示，有 (﹣2)×3= (﹣2)+(﹣2)+ (﹣2) = ﹣6.
类似地， (﹣2)×2= (﹣2)+(﹣2) = ﹣4. (﹣2)×1= . (﹣2)×0= .
异号两数相乘，只要把它们的绝对值相乘，符号取“﹣”.
根据上面的计算，你对一个负数乘一个正数有什么发现？一个负数乘0呢？
问题2 在问题1的情况下，问1 min前、2 min前该种生物标本的温度各是多少？
这里，以“现在”为基准，把以后时间记作“﹢”，以前时间记作“﹣”，那么1 min前记作﹣1，观察图可得，1 min前生物标本的温度是2℃，用算式表示，有
2min前（记作-2）生物标本的温度是1min前的2倍，可以写成
类似地，（﹣2）×（﹣3）= .
（﹣2）×（﹣1）=2.
（﹣2）×（﹣2）=4.
1.两数相乘，同号得正，异号得负，并把绝对值相乘.
2.任何数与0相乘仍得0.
解：(1) (-5)×(-6)=+(5×6)=30；
(4) 8×(-1.25)=-(8×1.25)=-10.
1.有理数乘法的求解步骤:
2.与小学所学一样，若两个有理数的乘积为1,我们称这两个有理数互为倒数.
注意： ①正数的倒数是正数，负数的倒数是负数； ②求小数的倒数，先化成分数，再求倒数； ③ 0没有倒数.
(1)35×(－4)； 　
(5)(－132.64)×0；
(2)(－8.125)×(－8)；　
(5)(6)(－6.1)×(＋6.1)．
(1)0.25×(－8)；
1.已知|x|＝3，|y|＝7，且xy<0，则x＋y＝ ．
2.若ab>0，且a＋b<0，则a 0，b 0.
3.若ab>0，且a＋b>0，则a 0，b 0.
问题 观察下列各式，它们的积是正还是负？(1)(－1)×2×3×4(2)(－1)×(－2)×3×4(3)(－1)×(－2)×(－3)×4(4)(－1)×(－2)×(－3)×(－4)(5)(－1)×(－2)×(－3)×(－4)×0
思考 多个有理数相乘，有一个因数为0，积是多少？因数都不为0时，积的符号和负因数的个数有什么关系？
－3的倒数为_______
几个数相乘，有一个因数为0，积为0.几个不为0的数相乘，积的符号由负因数的个数决定：当负因数的个数为奇数时，积为负；当负因数的个数为偶数时，积为正.
(1) 若abc>0，b、c异号，则a 0；(2) 在－6，－5，－1，3，4，7中任取三个数相乘，所得的积最小的是 ，最大的是 ．
1.三个数的乘积为0，则（ ） A.三个数一定都为0B.一个数为0，其他两个不为0C.至少有一个是0D.两个数为0，另一个不为0
解：（1）(- 3)×9×（-5） =3×9×5=135;
（2） |- 4| ×（- 0.2）=4×(-0.2)=-0.8;
（3） 8×2017× 0×(－6)=0；
4.用正负数表示气温的变化量，上升为正，下降为负.登山队攀登一座山峰，每登高1km，气温的变化量为-6℃，攀登3km后，气温有什么变化？
解：（-6）×3=-18(℃),答：气温下降18℃.
两数相乘，同号得正，异号得负，并把绝对值相乘.
任何数同0相乘，都得0.
几个不是零的数相乘，负因数的个数为奇数时,积为负数;偶数时,积为正数.
有一个因数为0，积为0.