2024年贵州省贵阳市花溪区高坡民族中学中考二模数学试题（原卷版）

这是一份2024年贵州省贵阳市花溪区高坡民族中学中考二模数学试题（原卷版），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

(限时：120分钟 总分：150分)
一、选择题(每小题3分，共36分．每小题均有A，B，C，D四个选项，其中只有一个选项正确)
1. 计算的结果是（ ）
A. B. 3C. 4D.
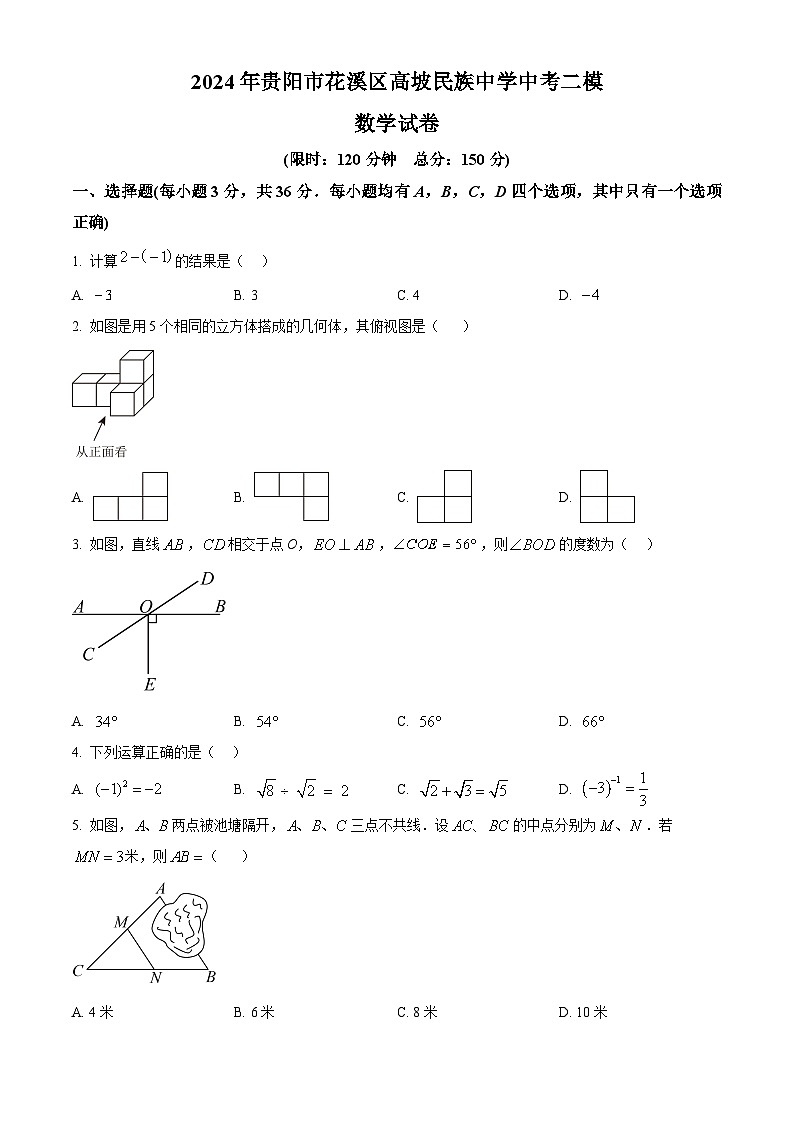
2. 如图是用5个相同的立方体搭成的几何体，其俯视图是（ ）
A. B. C. D.
3. 如图，直线，相交于点O，，，则的度数为（ ）
A. B. C. D.
4. 下列运算正确的是（ ）
A. B. C. D.
5. 如图，两点被池塘隔开，三点不共线．设的中点分别为．若米，则（ ）

A. 4米B. 6米C. 8米D. 10米
6. 将一个转盘分为均等的份，涂上如图所示的三种颜色，转动这个转盘时，转出可能性最小的颜色是（ ）
A 红B. 绿C. 黄D. 不确定
7. 若关于x的一元二次方程有实数根，则k的取值范围为（ ）
A. B. 且C. D. 且
8. 如图，在平行四边形中，，，以点B为圆心，适当长度为半径作弧，分别交，于点M，N，再分别以M，N为圆心，以大于的长为半径作弧，两弧相交于点P，作射线交于点，交的延长线于点，则的长为（ ）
A. 1B. C. D. 2
9. 某小区物业管委会一共有五名工作人员，已知这五名工作人员年龄分别为24，28，36，36，46(单位：岁)，随着小区入住人数的增多，现需增加一名工作人员，若增加后工作人员年龄的中位数小于原来工作人员年龄的中位数，则增加工作人员的年龄最大可以为（ ）
A 24岁B. 28岁C. 35岁D. 36岁
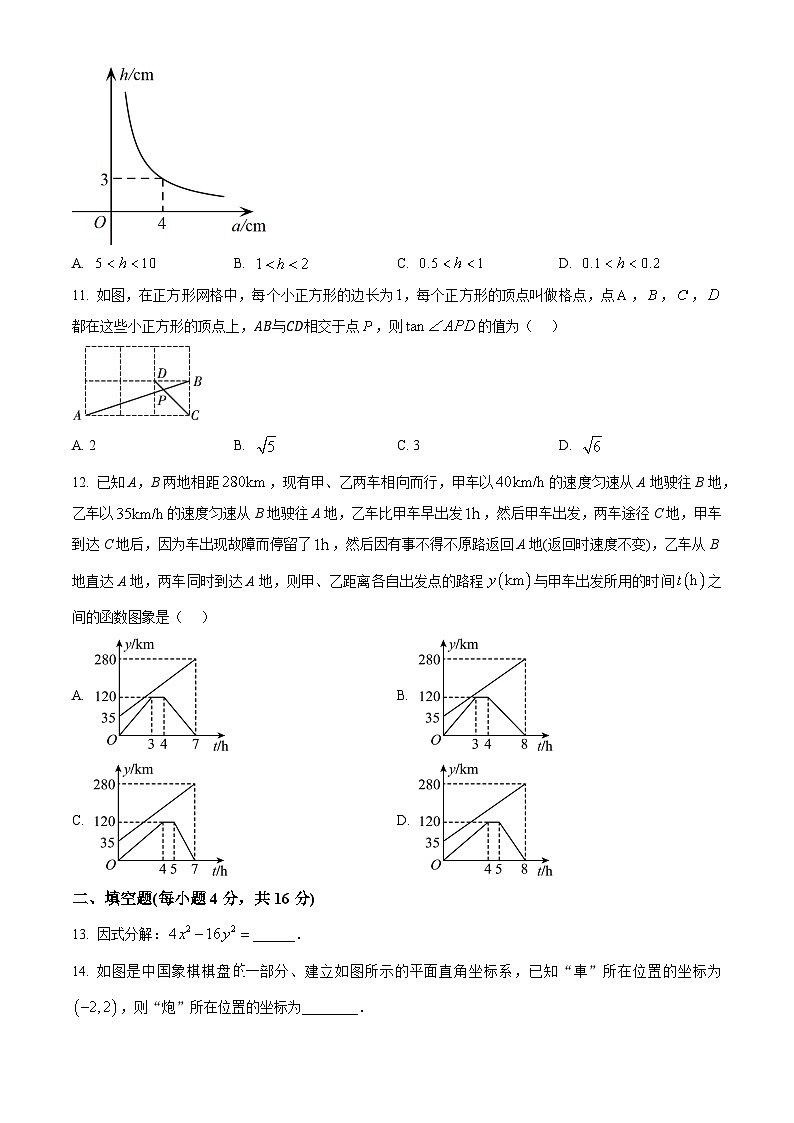
10. 当三角形面积一定时，它的底边长与底边上的高成反比例函数关系，其图像如图所示，则当底边长满足时，底边上的高的取值范围是（ ）
A. B. C. D.
11. 如图，在正方形网格中，每个小正方形的边长为，每个正方形的顶点叫做格点，点，，，都在这些小正方形的顶点上，AB与CD相交于点，则的值为（ ）
A. 2B. C. 3D.
12. 已知A，B两地相距，现有甲、乙两车相向而行，甲车以的速度匀速从A地驶往B地，乙车以的速度匀速从B地驶往A地，乙车比甲车早出发，然后甲车出发，两车途径C地，甲车到达C地后，因为车出现故障而停留了，然后因有事不得不原路返回A地(返回时速度不变)，乙车从B地直达A地，两车同时到达A地，则甲、乙距离各自出发点的路程与甲车出发所用的时间之间的函数图象是（ ）
A. B.
C. D.
二、填空题(每小题4分，共16分)
13. 因式分解：______．
14. 如图是中国象棋棋盘一部分、建立如图所示的平面直角坐标系，已知“車”所在位置的坐标为，则“炮”所在位置的坐标为________．
15. 小明一家准备用假期的两天去游玩，并且每天都要去一个不同的地方，现有三个地方可供选择，分别是“青岩古镇”“千户苗寨”“黄果树瀑布”，则小明一家这两天去了“青岩古镇”和“黄果树瀑布”的概率为________．
16. 在综合实践活动课上，老师以“正方形纸片的折叠”为主题开展数学活动．如图，下面是小星的操作步骤：第一步：将正方形纸片对折，使得与重合，展开铺平，折痕为．第二步：将正方形纸片再沿过点的直线折叠，使点落在上的点处，展开铺平，折痕与交于点，连接，则的值为________．
三、解答题(本大题共9题，共98分．解答应写出必要的文字说明、证明过程或演算步骤)
17. （1）解方程：；
（2）先化简，再求值：，其中x是满足范围内的整数．
18. 请根据下面对话，解答问题：
（1）设小明原来的速度为，则小明今天的速度为________；
（2）求小明今天的速度．
19. 校园消防关系到全校师生的生命安全．某校为加强学生的消防意识，开展了“消防安全知识”宣传活动，活动后举办了消防知识竞赛(百分制)，并分别在七、八年级中各随机抽取10名学生的成绩进行了统计、整理与分析(成绩用x表示，共分为三个等级：合格，良好，优秀)，下面给出了部分信息：
10名七年级学生的成绩：83，84，84，88，89，89，95，95，95，98
10名八年级学生中“良好”等级包含的所有数据为：85，90，90，90，94
抽取的七、八年级学生成绩统计表
抽取的八年级10名学生的成绩扇形统计图
（1）填空： ________， ________， ________；
（2）若该校八年级共有400名学生参加了此次竞赛，请估计该校八年级成绩不低于85分的人数；
（3）根据以上数据，你认为该校七、八年级中，哪个年级学生对消防知识掌握得更好？请说明理由，并对如何加强学生的消防意识写出一条你的看法．
20 如图，一次函数图象与反比例函数图象交于点，，与x轴交于点C，与y轴交于点D．

（1）求反比例函数与一次函数的解析式；
（2）点M在x轴上，若，求点M的坐标．
21. 在一次课题学习中，老师让同学们合作编题．某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解．
如图，将矩形的四边，CB，，AD分别延长至，，，，使得，，连接，，，．
（1）求证：；
（2）若矩形是边长为的正方形，且，，求的长．
22. 长期以来，冰雪运动被称为“高岭之花”．如图所示，滑雪轨道由两部分组成，轨道的长度都为200米，若AB与水平面的夹角，与水平面的夹角．
(参考数据：，，结果精确到1米)
（1）求轨道拐点B到轨道底端C的水平距离；
（2）若小星沿此轨道，从A处滑到C处，求小星下降的高度．
23. 如图，内接于，且AB为的直径，，与交于点，与过点的的切线交于点，交于点．
（1）求证：是等腰三角形；
（2）求证：；
（3）当点为DE的中点时，求的值．
24. 某公园要在圆形水池上修建喷泉，在池中心竖直水管的顶端安一个喷水头，使喷出的水柱呈抛物线型，如图所示，线段表示圆形水池的半径，以O为坐标原点，以线段所在直线为x轴，以水管所在直线为y轴，建立平面直角坐标系．按照设计师的设计，水管的高度为，且抛物线型水柱在与池中心的水平距离为处达到最高，且高度为，此时喷泉的观赏效果最佳．
（1）求抛物线型水柱的解析式；
（2）若此时有一个工人在清理水池，已知工人的身高为，求他站在距离A点多远以内会被水淋湿？
（3）为了使喷泉更加美观，如图所示，设计人员计划在中心水管上面延长一段增加一个喷水头，并使得该喷水头喷出的抛物线型水柱也在与池中心的水平距离为处达到最高，且比原抛物线水柱高，且落地处B点与点O的距离比短，则延长的水管高度应该设计为多少？
25. 综合与实践
问题情境
一节几何探究课上，老师提出如下问题：如图1，在菱形中，，点M在对角线上，点N在射线上，且，请猜想与的数量关系，并加以证明．
观察思考
（1）请解答老师提出的问题．
探索发现
（2）如图2，在图1的基础上连接，取的中点E，连接，．
①试猜想当点M与点A重合时，与之间的数量关系为_____________．
②当点M与点A不重合时，试探究①中结论是否仍成立，若成立，请加以证明：若不成立，请说明理由．
年级
平均数
中位数
众数
方差
“优秀等级”
所占百分比
七年级
90
89
a
26.6
八年级
90
b
90
30