数学九年级上册23.1 锐角的三角函数优质课课件ppt

这是一份数学九年级上册23.1 锐角的三角函数优质课课件ppt，共24页。PPT课件主要包含了旧知回顾，sinAcosB，由勾股定理可知等内容，欢迎下载使用。

使学生理解锐角正弦、余弦的定义．
会求直角三角形中锐角的正弦、余弦值．
求直角三角形中锐角的正弦、余弦值．
理解锐角正弦、余弦的定义；会求直角三角形中锐角的正弦、余弦值．
1．什么叫锐角的正切？什么叫坡度？如何表示？
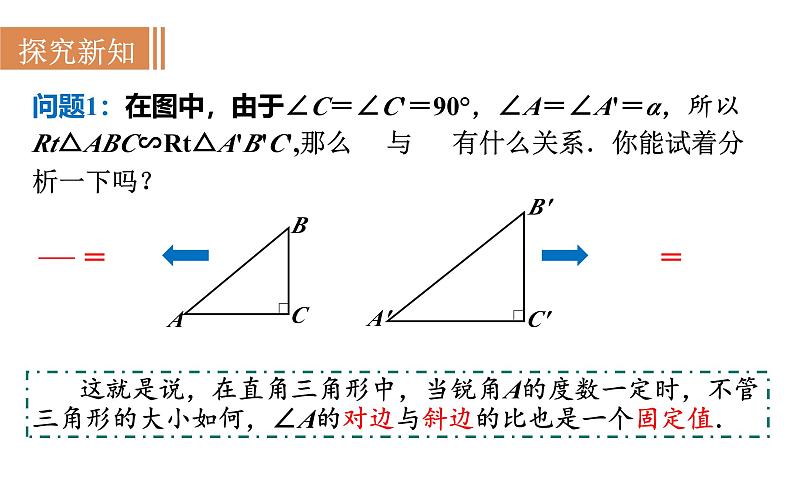
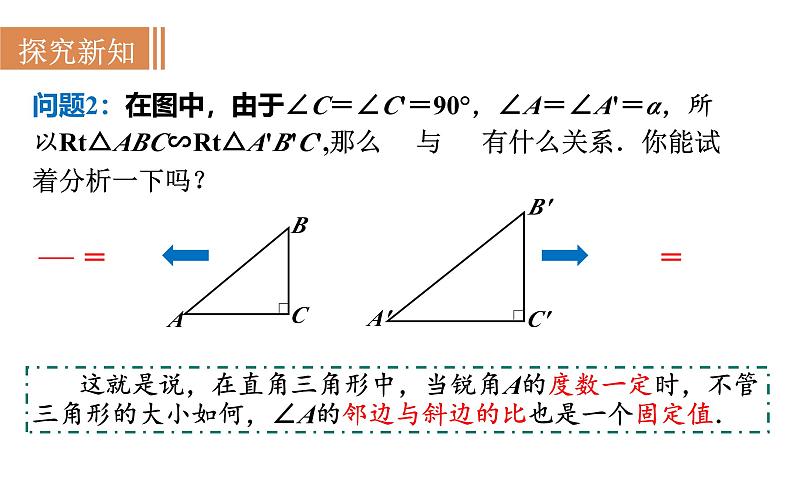
这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的对边与斜边的比也是一个固定值．
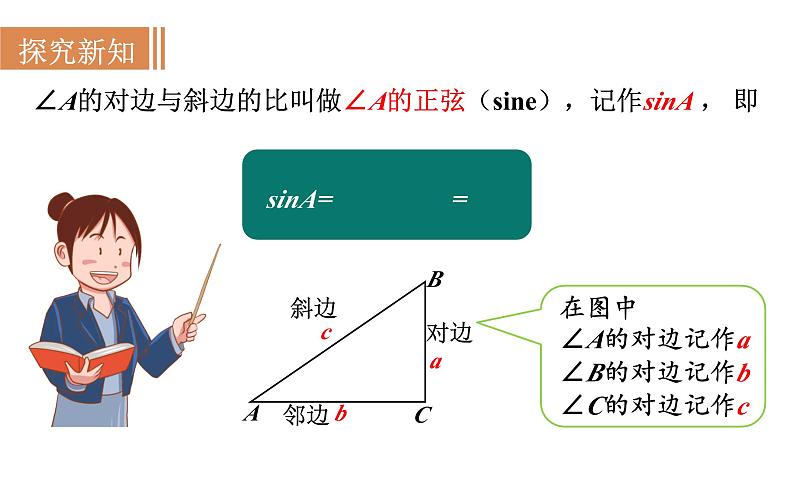
∠A的对边与斜边的比叫做∠A的正弦（sine），记作sinA ， 即
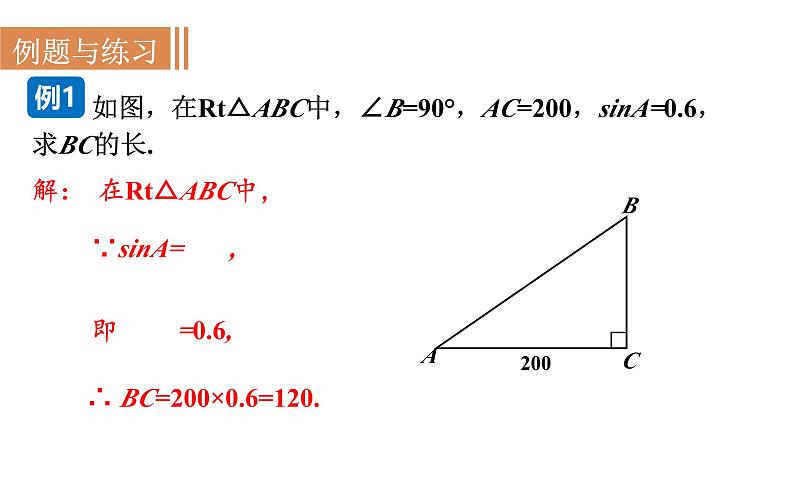
如图，在Rt△ABC中，∠B=90°，AC=200，sinA=0.6，求BC的长.
解： 在Rt△ABC中，
∴ BC=200×0.6=120.
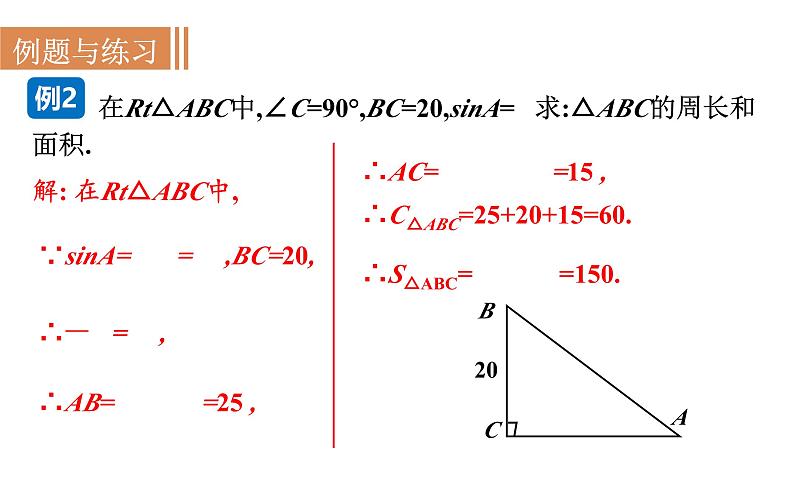
解: 在Rt△ABC中,
∴C△ABC=25+20+15=60.
这就是说，在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A的邻边与斜边的比也是一个固定值．
∠A的邻边与斜边的比叫做∠A的余弦（csine），记作csA，即
如图:在等腰△ABC中,AB=AC=5,BC=6.求:sinB,csB,tanB.
解：过A作AD⊥BC于D，则在Rt△ABD中
AB=5，已知BD=3,AD=4.
问题3：如图，梯子的倾斜程度与sinA和csA有关系吗？
sinA的值越大,梯子越陡;
csA的值越小,梯子越陡.
sin70°，cs70°，tan70°的大小关系是(　 )A．tan70°＜cs70°＜sin70°B．cs70°＜tan70°＜sin70° C．sin70°＜cs70°＜tan70°D．cs70°＜sin70°＜tan70°
解析：根据锐角三角函数的概念，知sin70°＜1，cs70°＜1，tan70°＞1.又cs70°＝sin20°，锐角的正弦值随着角的增大而增大，∴sin70°＞sin20°＝cs70°.故选D.
【方法总结】当角度在0°<∠A<90°间变化时，0csA>0.当角度在45°＜∠A＜90°间变化时，tanA＞1.
如图：在Rt △ABC中，∠C＝90°，
定义中应该注意的几个问题:
1.sinA,csA,tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形),csA,tanA是一个完整的符号,分别表示∠A的正弦,余弦,正切 (习惯省去“∠”号),csA,tanA 是一个比值.注意比的顺序.且sinA,csA,tanA均﹥0,无单位,csA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.5.角相等,则其三角函数值相等；两锐角的三角函数值相等,则这两个锐角相等.
在Rt△ABC中,∠C=90°,如图,已知AC=12,BC=5,求∠A的各个三角函数.
解：在Rt△ABC中，
∵AB=12，BC=5,∠C=90°，
思考:我们发现sinA=csB,其中的内在联系你可否掌握?
如图，在平面直角坐标系内有一点P（3，4），连接OP,求OP与x轴正方向所夹锐角α的各个三角函数.
解: 过点P作x轴的垂线，垂足为Q.
在Rt△PQO中，OQ=3，QP=4，得
4．如图，在正方形ABCD中，M是AD的中点，BE=3AE，求sin∠ECM.
解：设正方形ABCD的边长为4x，
∵M是AD的中点，BE=3AE，
∴AM＝DM＝2x,AE＝x,BE＝3x．
∴EM2=AM2+AE2=(2x)2+x2=5x2
∴CM2=DM2+DC2=(2x)2+(4x)2=20x2
∴EC2=BC2+BE2=(4x)2+(3x)2=25x2
∴EC2=EM2+CM2
△EMC为直角三角形.
由勾股定理逆定理可知，
5. 如图，在Rt△ABC中，∠C＝90°，AB =10，BC＝6，求sinA、csA、tanA的值．
∴设AC=15k，则AB=17k