三年（2022-2024）高考数学真题分类汇编（全国通用）专题09 平面向量（六大考点）（解析版）

这是一份三年（2022-2024）高考数学真题分类汇编（全国通用）专题09 平面向量（六大考点）（解析版），共14页。

考点1：平面向量线性运算
1．（2022年新高考全国I卷数学真题）在中，点D在边AB上，．记，则（ ）
A．B．C．D．
【答案】B
【解析】因为点D在边AB上，，所以，即，
所以．
故选：B．
考点2：数量积运算
2．（2022年高考全国甲卷数学（理）真题）设向量，的夹角的余弦值为，且，，则 ．
【答案】
【解析】设与的夹角为，因为与的夹角的余弦值为，即，
又，，所以，
所以．
故答案为：．
3．（2023年高考全国乙卷数学（文）真题）正方形的边长是2，是的中点，则（ ）
A．B．3C．D．5
【答案】B
【解析】方法一：以为基底向量，可知，
则，
所以；
方法二：如图，以为坐标原点建立平面直角坐标系，
则，可得，
所以；
方法三：由题意可得：，
在中，由余弦定理可得，
所以.
故选：B.
4．（2022年高考全国乙卷数学（理）真题）已知向量满足，则（ ）
A．B．C．1D．2
【答案】C
【解析】∵，
又∵
∴9，
∴
故选：C.
5．（2024年北京高考数学真题）设 ，是向量，则“”是“或”的（ ）．
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】B
【解析】因为，可得，即，
可知等价于，
若或，可得，即，可知必要性成立；
若，即，无法得出或，
例如，满足，但且，可知充分性不成立；
综上所述，“”是“且”的必要不充分条件.
故选：B.
考点3：求模问题
6．（2023年新课标全国Ⅱ卷数学真题）已知向量，满足，，则 ．
【答案】
【解析】法一：因为，即，
则，整理得，
又因为，即，
则，所以.
法二：设，则，
由题意可得：，则，
整理得：，即.
故答案为：.
7．（2024年新课标全国Ⅱ卷数学真题）已知向量满足，且，则（ ）
A．B．C．D．1
【答案】B
【解析】因为，所以，即，
又因为，
所以，
从而.
故选：B.
8．（2023年北京高考数学真题）已知向量满足，则（ ）
A．B．C．0D．1
【答案】B
【解析】向量满足，
所以.
故选：B
9．（2022年高考全国乙卷数学（文）真题）已知向量，则（ ）
A．2B．3C．4D．5
【答案】D
【解析】因为，所以.
故选：D
考点4：求夹角问题
10．（2023年高考全国甲卷数学（文）真题）已知向量，则（ ）
A．B．C．D．
【答案】B
【解析】因为，所以，
则，，
所以.
故选：B.
11．（2023年高考全国甲卷数学（理）真题）已知向量满足，且，则（ ）
A．B．C．D．
【答案】D
【解析】因为,所以,
即,即,所以.
如图,设,
由题知,是等腰直角三角形,
AB边上的高,
所以,
,
.
故选:D.
12．（2022年新高考全国II卷数学真题）已知向量，若，则（ ）
A．B．C．5D．6
【答案】C
【解析】,,即,解得,
故选：C
考点5：平行垂直问题
13．（2024年上海夏季高考数学真题））已知，且，则的值为 ．
【答案】15
【解析】，，解得．
故答案为：15．
14．（2024年新课标全国Ⅰ卷数学真题）已知向量，若，则（ ）
A．B．C．1D．2
【答案】D
【解析】因为，所以，
所以即，故，
故选：D.
15．（2022年高考全国甲卷数学（文）真题）已知向量．若，则 ．
【答案】/
【解析】由题意知：，解得.
故答案为：.
16．（2023年新课标全国Ⅰ卷数学真题）已知向量，若，则（ ）
A．B．
C．D．
【答案】D
【解析】因为，所以，，
由可得，，
即，整理得：．
故选：D．
17．（2024年高考全国甲卷数学（理）真题）设向量，则（ ）
A．“”是“”的必要条件B．“”是“”的必要条件
C．“”是“”的充分条件D．“”是“”的充分条件
【答案】C
【解析】对A，当时，则，
所以，解得或，即必要性不成立，故A错误；
对C，当时，，故，
所以，即充分性成立，故C正确；
对B，当时，则，解得，即必要性不成立，故B错误；
对D，当时，不满足，所以不成立，即充分性不立，故D错误.
故选：C.
考点6：平面向量取值与范围问题
18．（2024年天津高考数学真题）在边长为1的正方形中，点为线段的三等分点， ，则 ；为线段上的动点，为中点，则的最小值为 ．
【答案】
【解析】解法一：因为，即，则，
可得，所以；
由题意可知：，
因为为线段上的动点，设，
则，
又因为为中点，则，
可得
，
又因为，可知：当时，取到最小值；
解法二：以B为坐标原点建立平面直角坐标系，如图所示，
则，
可得，
因为，则，所以；
因为点在线段上，设，
且为中点，则，
可得，
则，
且，所以当时，取到最小值为；
故答案为：；.
19．（2023年高考全国乙卷数学（理）真题）已知的半径为1，直线PA与相切于点A，直线PB与交于B，C两点，D为BC的中点，若，则的最大值为（ ）
A．B．
C．D．
【答案】A
【解析】如图所示，，则由题意可知:，
由勾股定理可得
当点位于直线异侧时或PB为直径时，设，
则：
，则
当时，有最大值.
当点位于直线同侧时，设，
则：
，
，则
当时，有最大值.
综上可得，的最大值为.
故选：A.
20．（2022年新高考北京数学高考真题）在中，．P为所在平面内的动点，且，则的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】依题意如图建立平面直角坐标系，则，，，
因为，所以在以为圆心，为半径的圆上运动，
设，，
所以，，
所以
，其中，，
因为，所以，即；
故选：D
21．（2022年新高考天津数学高考真题）在中，，D是AC中点，，试用表示为 ，若，则的最大值为
【答案】
【解析】方法一：
，，
，当且仅当时取等号，而，所以．
故答案为：；．
方法二：如图所示，建立坐标系：
，，
，所以点的轨迹是以为圆心，以为半径的圆，当且仅当与相切时，最大，此时．
故答案为：；．
22．（2022年新高考浙江数学高考真题）设点P在单位圆的内接正八边形的边上，则的取值范围是 ．
【答案】
【解析】以圆心为原点，所在直线为轴，所在直线为轴建立平面直角坐标系，如图所示：
则,，设,于是，
因为，所以，故的取值范围是.
故答案为：．
23．（2023年天津高考数学真题）在中，，，记，用表示 ；若，则的最大值为 ．
【答案】
【解析】空1：因为为的中点，则，可得，
两式相加，可得到，
即，则；
空2：因为，则，可得，
得到，
即，即.
于是.
记，
则，
在中，根据余弦定理：，
于是，
由和基本不等式，，
故，当且仅当取得等号，
则时，有最大值.
故答案为：；.
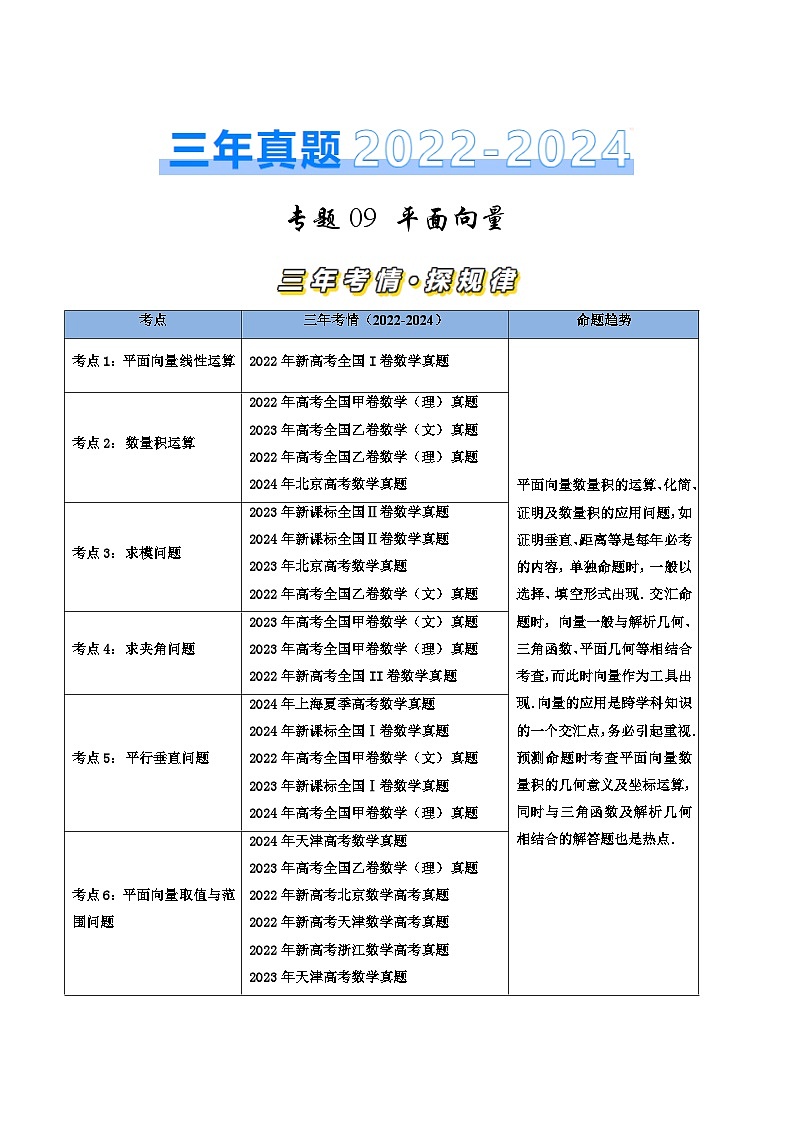
考点
三年考情（2022-2024）
命题趋势
考点1：平面向量线性运算
2022年新高考全国I卷数学真题
平面向量数量积的运算、化简、证明及数量积的应用问题，如证明垂直、距离等是每年必考的内容，单独命题时，一般以选择、填空形式出现．交汇命题时，向量一般与解析几何、三角函数、平面几何等相结合考查，而此时向量作为工具出现．向量的应用是跨学科知识的一个交汇点，务必引起重视．
预测命题时考查平面向量数量积的几何意义及坐标运算，同时与三角函数及解析几何相结合的解答题也是热点．
考点2：数量积运算
2022年高考全国甲卷数学（理）真题
2023年高考全国乙卷数学（文）真题
2022年高考全国乙卷数学（理）真题
2024年北京高考数学真题
考点3：求模问题
2023年新课标全国Ⅱ卷数学真题
2024年新课标全国Ⅱ卷数学真题
2023年北京高考数学真题
2022年高考全国乙卷数学（文）真题
考点4：求夹角问题
2023年高考全国甲卷数学（文）真题
2023年高考全国甲卷数学（理）真题
2022年新高考全国II卷数学真题
考点5：平行垂直问题
2024年上海夏季高考数学真题
2024年新课标全国Ⅰ卷数学真题
2022年高考全国甲卷数学（文）真题
2023年新课标全国Ⅰ卷数学真题
2024年高考全国甲卷数学（理）真题
考点6：平面向量取值与范围问题
2024年天津高考数学真题
2023年高考全国乙卷数学（理）真题
2022年新高考北京数学高考真题
2022年新高考天津数学高考真题
2022年新高考浙江数学高考真题
2023年天津高考数学真题