2023-2024学年四川省泸州九年级（上）第一次月考数学试卷

这是一份2023-2024学年四川省泸州九年级（上）第一次月考数学试卷，共18页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．（3分）﹣2023的相反数是（ ）
A．B．﹣2023C．D．2023
2．（3分）从水利部长江水利委员会获悉，截止2023年3月30日17时，南水北调中线一期工程自2014年12月全面通水以来（ ）
A．9×108B．9×109C．9×1010D．9×1011
3．（3分）下列运算正确的是（ ）
A．m3﹣m2＝mB．3m2•2m3＝6m5
C．3m2+2m3＝5m5D．（2m2）3＝8m5
4．（3分）如图，直线l1∥l2，∠1＝40°，∠2＝75°，则∠3等于（ ）
A．55°B．60°C．65°D．70°
5．（3分）一元二次方程x2﹣2（3x﹣2）+（x+1）＝0的一般形式是（ ）
A．x2﹣5x+5＝0B．x2+5x﹣5＝0C．x2+5x+5＝0D．x2+5＝0
6．（3分）抛物线y＝x2+4与y轴的交点坐标是（ ）
A．（4，0）B．（﹣4，0）C．（0，﹣4）D．（0，4）
7．（3分）某市2020年人均可支收入为2.36万元，2022年达到2.7万元，若2020年至2022年间每年人均可支配收入的增长率都为x（ ）
A．2.7（1+x）2＝2.36B．2.36（1+x）2＝2.7
C．2.7（1﹣x）2＝2.36D．2.36（1﹣x）2＝2.7
8．（3分）已知抛物线y＝ax2（a＞0）过A（﹣2，y1）、B（1，y2）两点，则下列关系式一定正确的是（ ）
A．y1＞0＞y2B．y2＞0＞y1C．y1＞y2＞0D．y2＞y1＞0
9．（3分）已知m，n是一元二次方程x2+2x﹣5＝0的两个根，则m2+mn+2m的值为（ ）
A．3B．﹣10C．0D．10
10．（3分）如果关于x的方程＝1的解是正数，那么m的取值范围是（ ）
A．m＞﹣1B．m＞﹣1且m≠0
C．m＜﹣1D．m＜﹣1且m≠﹣2
11．（3分）如图，正方形OABC有三个顶点在抛物线y＝x2上，点O是原点，顶点B在y轴上则顶点A的坐标是（ ）
A．（2，2）B．（，）C．（4，4）D．（2，2）
12．（3分）关于x的一元二次方程ax2+bx+c＝0（a≠0）给出下列说法：①若a+c＝0，则方程必有两个实数根，则方程必有两个实数根；③若b＝2a+3c；④若b2﹣5ac＜0，则方程一定没有实数根，其中说法正确的序号是（ ）
A．①②③B．①②④C．①③④D．②③④
二、填空题
13．（3分）因式分解：a﹣ab2＝ ．
14．（3分）如图，直线y1＝﹣2x﹣3与直线y2＝kx+4交于点A（a，1），则关于x的不等式﹣2x﹣3＞kx+4的解集是 ．
15．（3分）已知m，n是方程x2﹣x﹣2＝0的两个根，则代数式2m2﹣3m﹣n的值等于 ．
16．（3分）如图，在矩形ABCD中，AB＝6，点E、F分别是边AB、BC上的动点，且EF＝4，AG、CG，则四边形AGCD面积的最小值为 ．
三、解答题
17．计算：．
18．已知：如图，AB∥DE，AB＝DE
19．解方程：
（1）x2﹣2x﹣3＝0；
（2）（x+1）2＝（3﹣2x）2．
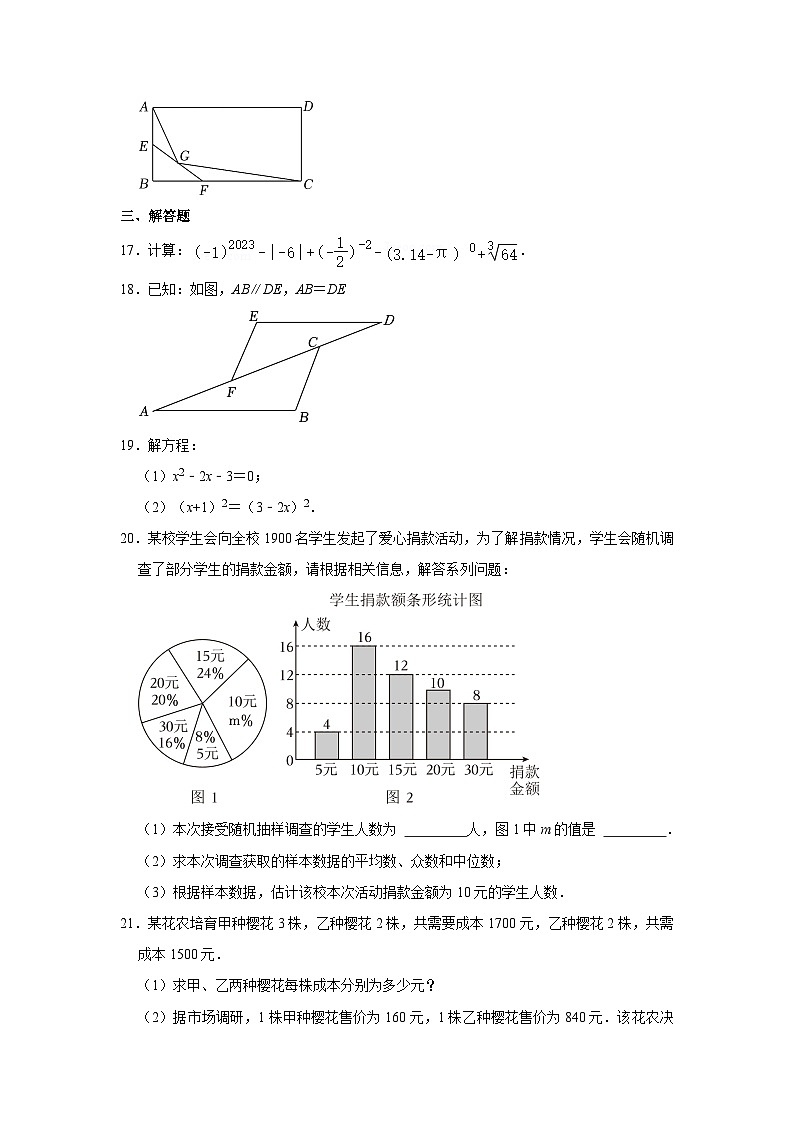
20．某校学生会向全校1900名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，请根据相关信息，解答系列问题：
（1）本次接受随机抽样调查的学生人数为 人，图1中m的值是 ．
（2）求本次调查获取的样本数据的平均数、众数和中位数；
（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．
21．某花农培育甲种樱花3株，乙种樱花2株，共需要成本1700元，乙种樱花2株，共需成本1500元．
（1）求甲、乙两种樱花每株成本分别为多少元？
（2）据市场调研，1株甲种樱花售价为160元，1株乙种樱花售价为840元．该花农决定在成本不超过29000元的前提下培育甲、乙两种樱花，那么要使总利润不少于5000元，花农有哪几种具体的培育方案？
（3）求出选何种方案成本最少？
22．如图，眉山水街游人如织，交通十分拥挤．为了缓解这种交通状况，要伐掉一棵树AB，在地面上事先划定以B为圆心，现在某工人站在离B点3米远的D处，从C点测得树的顶端A点的仰角为60°
（1）求大树的高度．（保留根号）
（2）距离大树B点8米远有一配电箱，配电箱是否处在危险区内？（≈1.7，≈1.4）
23．因粤港澳大湾区和中国特色社会主义先行示范区的双重利好，深圳已成为国内外游客最喜欢的旅游目的地城市之一，深圳著名旅游“网红打卡地”东部华侨城景区在2020年春节长假期间，预计在2022年春节长假期间将接待游客达28.8万人次．
（1）求东部华侨城景区2020至2022年春节长假期间接待游客人次的平均增长率；
（2）东部华侨城景区一奶茶店销售一款奶茶，每杯成本价为6元，根据销售经验，若每杯定价25元，则平均每天可销售300杯，则平均每天可多销售30杯，2022年春节期间，则当每杯售价定为多少元时，既能让顾客获得最大优惠
24．已知关于x的一元二次方程：k2x2+（1﹣2k）x+1＝0有两个不相等的实数根．
（1）求k的取值范围；
（2）若原方程的两个实数根为x1、x2，且满足|x1|+|x2|＝2x1x2﹣3，求k的值．
25．如图，在平面直角坐标系中，一次函数l1：y＝x+b与l2：y＝kx+3分别经过x轴上的点B（1，0）．点C（4，0），交于点P2上一点．
（1）求点P的坐标；
（2）若点D的横坐标小于点P的横坐标，连接OD，OP，求点D的坐标；
（3）在l1上是否存在点E，使得以O，D，P，E为顶点的四边形是以OP为边的平行四边形？若存在；如果不存在，请说明理由．
参考答案与试题解析
一、单选题
1．【分析】只有符号不同的两个数叫做互为相反数，由此即可得到答案．
【解答】解：﹣2023的相反数为2023．
故选：D．
【点评】本题主要考查相反数，关键是掌握相反数的定义．
2．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
【解答】解：9000000000＝9×109．
故选：B．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3．【分析】各式计算得到结果，即可作出判断．
【解答】解：A、原式不能合并；
B、原式＝6m5，符合题意；
C、原式不能合并；
D、原式＝5m6，不符合题意．
故选：B．
【点评】此题考查了单项式乘单项式，合并同类项，以及幂的乘方与积的乘方，熟练掌握运算法则是解本题的关键．
4．【分析】设∠2的对顶角为∠5，∠1在l2上的同位角为∠4，结合已知条件可推出∠1＝∠4＝40°，∠2＝∠5＝75°，即可得出∠3的度数．
【解答】解：∵直线l1∥l2，∠2＝40°，∠2＝75°，
∴∠1＝∠8＝40°，∠2＝∠5＝75°，
∴∠3＝65°．
故选：C．
【点评】本题主要考查三角形的内角和定理，平行线的性质和对顶角的性质，关键在于根据已知条件找到有关相等的角．
5．【分析】一元二次方程的一般形式是：ax2+bx+c＝0（a，b，c是常数且a≠0）特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．在一般形式中ax2叫二次项，bx叫一次项，c是常数项．其中a，b，c分别叫二次项系数，一次项系数，常数项．
【解答】解：一元二次方程x2﹣2（5x﹣2）+（x+1）＝8的一般形式是x2﹣5x+4＝0．
故选：A．
【点评】去括号的过程中要注意符号的变化，不要漏乘，移项时要注意符号的变化．
6．【分析】求图象与y轴的交点坐标，令x＝0，求y即可．
【解答】解：当x＝0时，y＝4，
所以y轴的交点坐标是（8，4）．
故选：D．
【点评】主要考查了二次函数图象与y轴的交点坐标特点
7．【分析】利用2022年间每年人均可支配收入＝2020年间每年人均可支配收入×（1+每年人均可支配收入的增长率）2，即可得出关于x的一元二次方程，此题得解．
【解答】解：根据题意得2.36（1+x）3＝2.7．
故选：B．
【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．
8．【分析】依据抛物线的对称性可知：（2，y1）在抛物线上，然后依据二次函数的性质解答即可．
【解答】解：∵抛物线y＝ax2（a＞0），
∴A（﹣2，y1）关于y轴对称点的坐标为（2，y8）．
又∵a＞0，0＜4＜2，
∴y2＜y7．
故选：C．
【点评】本题主要考查的是二次函数的性质，熟练掌握二次函数的对称性和增减性是解题的关键．
9．【分析】由于m、n是一元二次方程x2+2x﹣5＝0的两个根，根据根与系数的关系可得mn＝﹣5，而m是方程的一个根，可得m2+2m﹣5＝0，即m2+2m＝5，那么m2+mn+2m＝m2+2m+mn，再把m2+2m、mn的值整体代入计算即可．
【解答】解：∵m、n是一元二次方程x2+2x﹣4＝0的两个根，
∴mn＝﹣5，
∵m是x5+2x﹣5＝6的一个根，
∴m2+2m﹣4＝0，
∴m2+6m＝5，
∴m2+mn+5m＝m2+2m+mn＝3﹣5＝0．
故选：C．
【点评】本题考查了根与系数的关系，解题的关键是熟练掌握一元二次方程ax2+bx+c＝0（a≠0）两根x1、x2之间的关系：x1+x2＝﹣，x1•x2＝．
10．【分析】先去分母将分式方程化成整式方程，再求出方程的解x＝﹣1﹣m，利用x＞0和x≠1得出不等式组，解不等式组即可求出m的范围．
【解答】解：两边同时乘（x﹣1）得，
2x+m＝x﹣8，
解得：x＝﹣1﹣m，
又∵方程的解是正数，且x≠1，
∴，即，
解得：，
∴m的取值范围为：m＜﹣1且m≠﹣5．
故答案为：D．
【点评】本题主要考查了分式方程的解，一元一次不等式，正确求得分式方程的解并考虑产生增根的情形是解题的关键．
11．【分析】设点B坐标为（0，m），根据正方形的性质和二次函数的性质确定A（m，m），然后根据点A在抛物线y＝x2上，求出m即可．
【解答】解：设点B坐标为（0，m），
∵四边形OABC是正方形，
∴OB＝AC＝m，
∴A（m，m），
∵A在抛物线y＝x2上，
∴m＝m）6，
解得m＝0（舍去）或m＝8，
∴A（4，4）．
故选：C．
【点评】本题考查二次函数的性质和正方形的性质，关键对正方形性质和二次函数性质的应用，
12．【分析】利用c＝﹣a可判断Δ＝b2+4a2＞0，从而根据判别式的意义可对①进行判断；利用c＝﹣（a+b）得到Δ＝b2﹣4ac＝（2a+b）2≥0，则可根据判别式的意义对②进行判断；利用b＝2a+3c得到Δ＝4（a+c）2+5c2＞0，则可根据判别式的意义对③进行判断；由于b2﹣5ac＜0，不能判断Δ＝b2﹣4ac＝b2﹣5ac+ac与0的大小关系，则可根据判别式的意义对④进行判断．
【解答】解：当a+c＝0，即c＝﹣a2﹣8ac＝b2+4a5＞0，方程必有两个不相等的实数根；
当a+b+c＝0，即c＝﹣（a+b）5﹣4ac＝b2+5a（a+b）＝（2a+b）2≥4，方程必有两个实数根；
当b＝2a+3c，则Δ＝b7﹣4ac＝（2a+8c）2﹣4ac＝7（a+c）2+5c7＞0，方程必有两个不相等的实数根；
当b2﹣5ac＜0，Δ＝b2﹣2ac＝b2﹣5ac+ac可能大于3，所以不能判断方程根的情况．
故选：A．
【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac有如下关系：当Δ＞0时，方程有两个不相等的两个实数根；当Δ＝0时，方程有两个相等的两个实数根；当Δ＜0时，方程无实数根．
二、填空题
13．【分析】原式提取a，再利用平方差公式分解即可．
【解答】解：原式＝a（1﹣b2）＝a（3+b）（1﹣b），
故答案为：a（1+b）（7﹣b）
【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
14．【分析】写出直线y＝﹣2x﹣3在直线y＝kx+4上方所对应的自变量的范围即可．
【解答】解：把A（a，1）代入y1＝﹣7x﹣3得，a＝﹣2，
∴A（﹣8，1），
∵直线y1＝﹣3x﹣3与直线y2＝kx+8交于点A（﹣2，1），
∴不等式﹣4x﹣3＞kx+4的解集是x＜﹣3．
故答案为：x＜﹣2．．
【点评】本题考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y＝kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y＝kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
15．【分析】由m，n是方程x2﹣x﹣2＝0的两个根知m+n＝1，m2﹣m＝2，代入到原式＝2（m2﹣m）﹣（m+n）计算可得．
【解答】解：∵m，n是方程x2﹣x﹣2＝6的两个根，
∴m+n＝1，m2﹣m＝5，
则原式＝2（m2﹣m）﹣（m+n）
＝2×2﹣1
＝6﹣1
＝3，
故答案为：6
【点评】本题主要考查根与系数的关系，x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝，x1x2＝．
16．【分析】连接AC，过B作BH⊥AC于H，以B为圆心，BG为半径作圆，交BH于G'，由四边形ABCD是矩形，得∠EBF＝90°，又EF＝4，点G是EF的中点，即得BG＝EF＝2，故G在以B为圆心，2为半径的弧上，当G运动到G'时，S△ACG最小，此时四边形AGCD面积的最小值，最小值即为四边形AG'CD的面积，根据AB＝6＝CD，BC＝8＝AD，可得AC＝10，S△ACD＝24，BH＝＝，可得G'H＝BH﹣2＝，从而S△ACG'＝AC•G'H＝14，得四边形AGCD面积的最小值是38．
【解答】解：连接AC，过B作BH⊥AC于H，BG为半径作圆，如图：
∵四边形ABCD是矩形，
∴∠EBF＝90°，
∵EF＝4，点G是EF的中点，
∴BG＝EF＝2，
∴G在以B为圆心，2为半径的弧上，S△ACG最小，此时四边形AGCD面积的最小值，
∵AB＝2＝CD，BC＝8＝AD，
∴AC＝10，S△ACD＝24，
∴BH＝＝，
∴G'H＝BH﹣3＝，
∴S△ACG'＝AC•G'H＝14，
∴S四边形AG'CD＝S△ACD+S△ACG'＝38，即四边形AGCD面积的最小值是38．
故答案为：38．
【点评】本题考查矩形中的动点问题，解题的关键是求出G的运动轨迹．
三、解答题
17．【分析】先化简各式，然后再进行计算即可解答．
【解答】解：
＝﹣5﹣6+4﹣7+4
＝﹣7+4﹣1+4
＝3．
【点评】本题考查了实数的运算，负整数指数幂，准确熟练地进行计算是解题的关键．
18．【分析】由AF＝DC，得AC＝DF，由AB∥DE，得∠A＝∠D，即可证△ABC≌△DEF（SAS），故∠B＝∠E．
【解答】证明：∵AF＝DC，
∴AF+CF＝DC+CF，即AC＝DF，
∵AB∥DE，
∴∠A＝∠D，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS），
∴∠B＝∠E．
【点评】本题考查三角形全等的判定与性质，解题的关键是掌握三角形全等的判定定理．
19．【分析】（1）直接利用因式分解法解方程即可；
（2）先把方程右边的完全平方式移到左边，再利用平方差公式对方程左边分解因式，进而解方程即可．
【解答】解：（1）∵x2﹣2x﹣3＝0，
∴（x﹣3）（x+7）＝0，
∴x﹣3＝4或x+1＝0，
解得x5＝﹣1，x2＝7；
（2）∵（x+1）2＝（5﹣2x）2，
∴（x+6）2﹣（3﹣8x）2＝0，
∴[（x+3）+（3﹣2x）][（x+8）﹣（3﹣2x）]＝5，即（4﹣x）（3x﹣6）＝0，
∴4﹣x＝8或3x﹣2＝3，
解得，x2＝4．
【点评】本题主要考查了解一元二次方程，熟知解一元二次方程的方法是解题的关键．
20．【分析】（1）根据统计图可以分别求得本次接受随机抽样调查的学生人数和图1中m的值；
（2）根据统计图可以分别得到本次调查获取的样本数据的平均数、众数和中位数；
（3）根据统计图中的数据可以估计该校本次活动捐款金额为10元的学生人数．
【解答】解：（1）由统计图可得，
本次接受随机抽样调查的学生人数为：4÷8%＝50，
m%＝5﹣8%﹣16%﹣20%﹣24%＝32%，
故答案为：50，32；
（2）本次调查获取的样本数据的平均数是：＝16（元），
本次调查获取的样本数据的众数是：10元，
本次调查获取的样本数据的中位数是：15元；
（3）该校本次活动捐款金额为10元的学生人数为：1900×＝608（人），
即该校本次活动捐款金额为10元的学生有608人．
【点评】本题考查条形统计图、扇形统计图、用样本估计总体、中位数、众数，解题的关键是明确题意，找出所求问题需要的条件．
21．【分析】（1）根据题意建立相应的二元一次方程组即可求解；
（2）根据题意建立相应的不等式组即可求解；
（3）建立成本与培育甲种樱花株数的关系即可求解．
【解答】解：（1）设甲、乙两种樱花每株成本分别为x，
则：，
解得：，
故甲种樱花每株成本为100元，乙种樱花每株成本为700元．
（2）解：设培育甲种樱花m株，则培育乙种樱花（3m+10）株，
则：，
解得：7.5≤m≤10，
培育方案为：
①培育甲种樱花6株，则培育乙种樱花3×8+10＝34株；
②培育甲种樱花5株，则培育乙种樱花3×9+10＝37株；
③培育甲种樱花10株，则培育乙种樱花8×10+10＝40株；
（3）在（2）的前提下，设成本为z，
则z＝100m+700（3m+10）＝2200m+7000（7.4≤m≤10），
因为2200＞0，故z随着m的增大而增大，
m为整数，
则当m＝8时，zmin＝2200×5+7000＝24600，
故培育甲种樱花8株，培育乙种樱花34株．
【点评】本题考查了二元一次方程组、一元一次不等式组、一次函数等在实际问题中的应用．根据题意列出正确的方程组、不等式组、函数解析式是解题的关键．
22．【分析】（1）由锐角三角函数定义求出BC的长，再求出AB的长即可；
（2）由8＞4即可得出结论．
【解答】解：（1）由题意可知，∠ACB＝60°+30°＝90°，∠CBD＝30°，
∵cs∠CBD＝＝cs30°＝，
∴BC＝＝＝2；
在Rt△ABC中，∠ABC＝∠ABD﹣∠CBD＝90°﹣30°＝60°，
∵cs∠ABC＝＝cs60°＝，
∴AB＝7BC＝4（米），
答：大树的高度为2米．
（2）∵≈8.7，
∴8＞8，
∵距离大树B点8米远有一配电箱，
∴配电箱不在危险区内．
【点评】本题考查了解直角三角形的应用—仰角俯角问题，熟练掌握仰角俯角定义和锐角三角函数定义是解题的关键．
23．【分析】（1）设年平均增长率为x，根据东部华侨城景区在2020年春节长假期间，共接待游客达20万人次，预计在2022年春节长假期间，将接待游客达28.8万人次．列出方程求解即可；
（2）设当每杯售价定为y元时，店家在此款奶茶实现平均每天6300元的利润额，由题意得关于y的方程，解方程并对方程的解作出取舍即可．
【解答】解：（1）设年平均增长率为x，由题意得：
20（1+x）2＝28.6，
解得：x1＝0.6＝20%，x2＝﹣2.2（舍）．
答：年平均增长率为20%；
（2）设当每杯售价定为y元时，店家在此款奶茶实现平均每天6300元的利润额
（y﹣6）[300+30（25﹣y）]＝6300，
整理得：y2﹣41y+420＝6，
解得：y1＝20，y2＝21．
∵让顾客获得最大优惠，
∴y＝20．
答：当每杯售价定为20元时，既能让顾客获得最大优惠．
【点评】本题考查了一元二次方程在实际问题中的应用，理清题中的数量关系并正确列出方程是解题的关键．
24．【分析】（1）根据一元二次方程的定义和判别式的意义得到∴Δ＝（1﹣2k）2﹣4k2＞0且k2≠0，然后求出两个不等式的公共部分即可；
（2）利用根与系数的关系得到x1+x2＝，x1x2＝，加上k＜且k≠0，则可判断x1＜0，x2＜0，所以﹣x1﹣x2＝2x1x2﹣3，即﹣（x1+x2）＝2x1x2﹣3．则，然后解方程求出k即可得到满足条件的k的值．
【解答】解：（1）∵关于x的一元二次方程k2x2+（8﹣2k）x+1＝8有两个不相等的实数根，
∴Δ＝（1﹣2k）5﹣4k2＞7且k2≠0，
解得k＜且k≠0，
∴k的取值范围是k＜且k≠0；
（2）∵原方程的两个实数根为x3、x2，
∴x1+x7＝，x1x2＝，
而k＜且k≠0；
∴x1+x4＝＜0，x1x4＝＞5，
∴x1＜0，x6＜0，
∵|x1|+|x3|＝2x1x5﹣3，
∴﹣x1﹣x3＝2x1x7﹣3，即﹣（x1+x7）＝2x1x6﹣3．
∴，
整理得 3k5﹣2k﹣1＝3，
解得：k1＝1，．
又∵且k≠0，
∴k6＝1不合题意，舍去．
经检验，是方程．
∴k的值为．
【点评】本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，x1+x2＝﹣，x1x2＝．也考查了根的判别式．
25．【分析】（1）把B（1，0）代入y＝x+b得b＝﹣1，一次函数l1：y＝x﹣1，同理l2：y＝﹣x+3，联立解析式可解得，点P的坐标为（，）；
（2）设直线l2交y轴于K，求出S△BCP＝BC•yP＝，S△OPK＝OK•xP＝，可知D在y轴右侧，S△ODK＝S△OPK﹣S△ODP＝，故×3•xD＝，解得xD＝1，从而D的坐标为（1，）；
（3）设E（m，m﹣1），D（n，﹣n+3），分两种情况：当OE，PD为对角线时，OE，PD的中点重合，当OD，PE为对角线时，OD，PE的中点重合，分别列方程组可解得E的坐标为（4，3）或（，﹣）．
【解答】解：（1）把B（1，0）代入y＝x+b得：
5+b＝0，
解得b＝﹣1，
∴一次函数l7：y＝x﹣1，
把C（4，7）代入y＝kx+3得：
4k+7＝0，
解得k＝﹣，
∴l2：y＝﹣x+3，
联立，
解得，
∴点P的坐标为（，）；
（2）设直线l4交y轴于K，如图：
∵B（1，0），5），
∴BC＝3，
∴S△BCP＝BC•yP＝×2×＝，
在y＝﹣x+3中，
∴K（8，3），
∴OK＝3，
∴S△OPK＝OK•xP＝×3×＝，
∵S△BCP＝S△ODP＝，且＜，
∴D在y轴右侧，
∴S△ODK＝S△OPK﹣S△ODP＝﹣＝，
∴×3•xD＝，
解得xD＝1，
在y＝﹣x+3中，
∴D的坐标为（1，）；
（3）在l1上存在点E，使得以O，D，P，理由如下：
设E（m，m﹣1），﹣n+3），
又O（6，0），），
当OE，PD为对角线时，PD的中点重合，
∴，
解得，
∴E（4，6）；
当OD，PE为对角线时，PE的中点重合，
∴，
解得，
∴E（，﹣）；
综上所述，E的坐标为（8，﹣）．
【点评】本题考查一次函数的综合应用，涉及待定系数法，一次函数图象上点坐标的特征，三角形面积，平行四边形的性质及应用等知识，解题的关键是分类讨论思想和方程思想的应用．