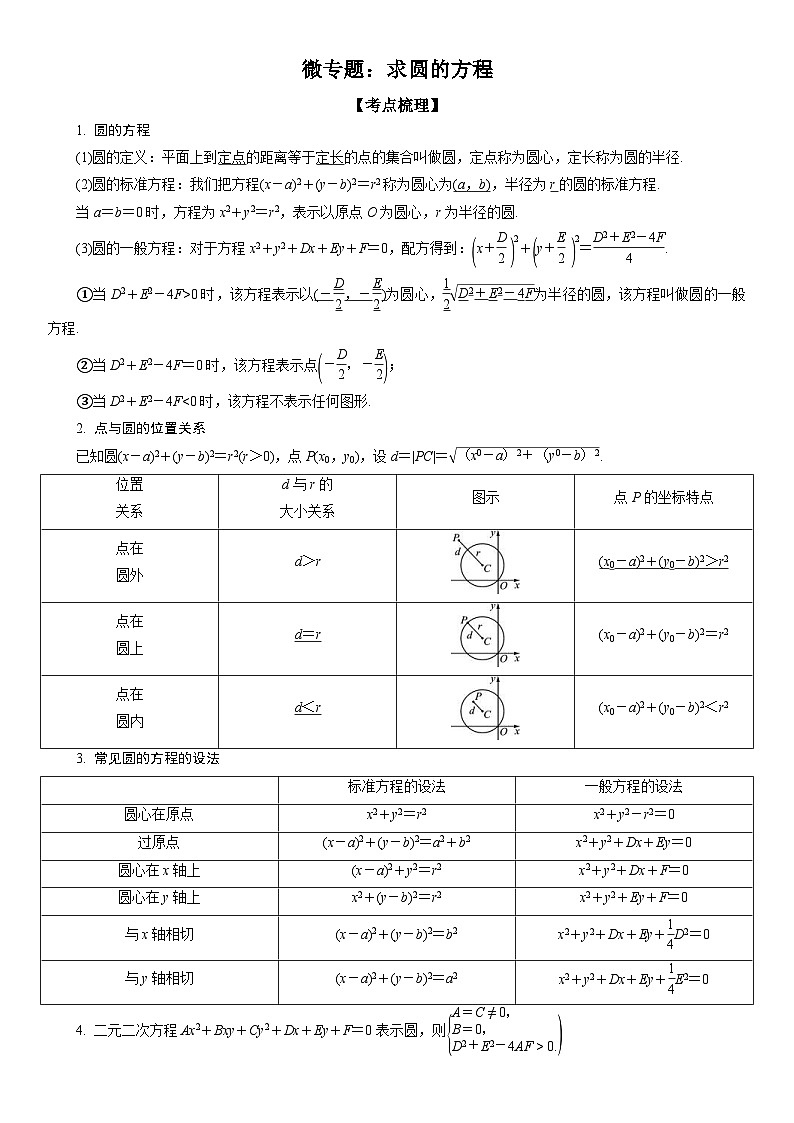
新高考数学一轮复习考点过关练习 求圆的方程（含解析）

这是一份新高考数学一轮复习考点过关练习 求圆的方程（含解析），共26页。

1. 圆的方程
(1)圆的定义：平面上到定点的距离等于定长的点的集合叫做圆，定点称为圆心，定长称为圆的半径.
(2)圆的标准方程：我们把方程(x－a)2＋(y－b)2＝r2称为圆心为(a，b)，半径为r的圆的标准方程.
当a＝b＝0时，方程为x2＋y2＝r2，表示以原点O为圆心，r为半径的圆.
(3)圆的一般方程：对于方程x2＋y2＋Dx＋Ey＋F＝0，配方得到：eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(D,2)))eq \s\up12(2)＋eq \b\lc\(\rc\)(\a\vs4\al\c1(y＋\f(E,2)))eq \s\up12(2)＝eq \f(D2＋E2－4F,4).
①当D2＋E2－4F>0时，该方程表示以(－eq \f(D,2)，－eq \f(E,2))为圆心，eq \f(1,2)eq \r(D2＋E2－4F)为半径的圆，该方程叫做圆的一般方程.
②当D2＋E2－4F＝0时，该方程表示点eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(D,2)，－\f(E,2)))；
③当D2＋E2－4F<0时，该方程不表示任何图形.
2. 点与圆的位置关系
已知圆(x－a)2＋(y－b)2＝r2(r＞0)，点P(x0，y0)，设d＝|PC|＝eq \r(（x0－a）2＋（y0－b）2).
3. 常见圆的方程的设法
4. 二元二次方程Ax2＋Bxy＋Cy2＋Dx＋Ey＋F＝0表示圆，则eq \b\lc\{(\a\vs4\al\c1(A＝C≠0，,B＝0，,D2＋E2－4AF>0.))
5. 以A(x1，y1)，B(x2，y2)为直径端点的圆的方程为(x－x1)(x－x2)＋(y－y1)(y－y2)＝0.
6. 圆心为(a，b)，半径为r的圆的参数方程为eq \b\lc\{(\a\vs4\al\c1(x＝a＋rcsθ，,y＝b＋rsinθ，))其中θ为参数.
【题型归纳】
题型一： 圆的标准方程
1．经过三个点 SKIPIF 1 < 0 的圆的方程为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
2．圆 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称的圆的方程是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
3．已知圆 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 （ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）对称，则 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B．9C．4D．8
题型二： 圆的一般方程
4．已知圆 SKIPIF 1 < 0 与圆 SKIPIF 1 < 0 交于A、B两点，且 SKIPIF 1 < 0 平分圆 SKIPIF 1 < 0 的周长，则 SKIPIF 1 < 0 的值为（ ）
A．0B．2C．4D．6
5．设甲：实数 SKIPIF 1 < 0 ；乙：方程 SKIPIF 1 < 0 是圆，则甲是乙的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
6．若圆 SKIPIF 1 < 0 的弦MN的中点为 SKIPIF 1 < 0 ，则直线MN的方程是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型三： 点与圆的位置关系
7．已知直线 SKIPIF 1 < 0 ，圆 SKIPIF 1 < 0 ，则直线l与圆C的位置关系是（ ）
A．相离B．相切C．相交D．不确定
8．已知抛物线 SKIPIF 1 < 0 的焦点为 SKIPIF 1 < 0 ，圆 SKIPIF 1 < 0 的圆心 SKIPIF 1 < 0 在抛物线上，则点 SKIPIF 1 < 0 （ ）
A．在圆 SKIPIF 1 < 0 外B．在圆 SKIPIF 1 < 0 上
C．在圆 SKIPIF 1 < 0 内但不与点 SKIPIF 1 < 0 重合D．与点 SKIPIF 1 < 0 重合
9．已知点 SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 上，则直线 SKIPIF 1 < 0 与圆的位置关系是（ ）
A．相交B．相切C．相离D．无法判断
【双基达标】
10．圆 SKIPIF 1 < 0 的圆心坐标和半径分别是（ ）
A．(-1，0)，3B．(1，0)，3
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
11．已知圆 SKIPIF 1 < 0 的圆心在直线 SKIPIF 1 < 0 上，则该圆的面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
12．已知半径为1的圆经过点 SKIPIF 1 < 0 ，则其圆心到原点的距离的最小值为（ ）．
A．4B．5C．6D．7
13．方程 SKIPIF 1 < 0 表示圆，则实数a的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
14．若点 SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 的外部，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
15．已知两定点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若动点 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的轨迹为（ ）．
A．直线B．线段C．圆D．半圆
16．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
17．已知圆 SKIPIF 1 < 0 ，则当圆 SKIPIF 1 < 0 的面积最小时，圆上的点到坐标原点的距离的最大值为（ ）
A． SKIPIF 1 < 0 B．6
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
18．“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 为圆方程”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分又不必要条件
19．已知方程x2＋y2－2x＋2k＋3＝0表示圆，则k的取值范围是（ ）
A．(－∞，－1)
B．(3，＋∞)
C．(－∞，－1)∪(3，＋∞)
D． SKIPIF 1 < 0
20．当方程 SKIPIF 1 < 0 所表示的圆的面积最大时，直线 SKIPIF 1 < 0 的倾斜角为（ ）．
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
21．若方程 SKIPIF 1 < 0 表示圆，则 SKIPIF 1 < 0 实数的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
22．已知 SKIPIF 1 < 0 是实常数，若方程 SKIPIF 1 < 0 表示的曲线是圆，则 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
23．点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 上 SKIPIF 1 < 0 ，且点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称，则该圆的半径为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．1D． SKIPIF 1 < 0
24．已知圆 SKIPIF 1 < 0 ，则当圆 SKIPIF 1 < 0 的面积最小时，圆上的点到坐标原点的距离的最大值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
25．如果复数z满足 SKIPIF 1 < 0 ，那么 SKIPIF 1 < 0 的最大值是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
26．若方程 SKIPIF 1 < 0 表示圆，则实数 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
27．圆心为 SKIPIF 1 < 0 ，半径为3的圆的方程是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
28．“ SKIPIF 1 < 0 ”是“点 SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 外”的（ ）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
29．方程x2+y2﹣kx+2y+k2﹣2＝0表示圆的一个充分不必要条件是（ ）
A．k∈(﹣∞，﹣2)∪(2，+∞)B．k∈(2，+∞)
C．k∈(﹣2，2)D．k∈(0，1]
30．已知M，N分别是曲线 SKIPIF 1 < 0 上的两个动点，P为直线 SKIPIF 1 < 0 上的一个动点，则 SKIPIF 1 < 0 的最小值为
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C．2D．3
【高分突破】
单选题
31．若方程 SKIPIF 1 < 0 表示圆，则实数 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
32．已知圆 SKIPIF 1 < 0 的圆心到直线 SKIPIF 1 < 0 的距离为 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
33．若实数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最大值是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
34．以直线 SKIPIF 1 < 0 经过的定点为圆心，2为半径的圆的方程是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
二、多选题
35．(多选)由方程x2＋y2＋x＋(m－1)y＋ SKIPIF 1 < 0 m2＝0所确定的圆的面积不能为（ ）
A． SKIPIF 1 < 0 πB． SKIPIF 1 < 0 π
C．πD．2π
36．若过点 SKIPIF 1 < 0 有两条直线与圆 SKIPIF 1 < 0 相切，则实数m的可能取值是（ ）
A．－3B．3C．0D． SKIPIF 1 < 0
37．已知二次函数 SKIPIF 1 < 0 交 SKIPIF 1 < 0 轴于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 两点（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 不重合），交 SKIPIF 1 < 0 轴于 SKIPIF 1 < 0 点.圆 SKIPIF 1 < 0 过 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 三点.下列说法正确的是（ ）
①圆心 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上；
② SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 ；
③圆 SKIPIF 1 < 0 半径的最小值为1；
④存在定点 SKIPIF 1 < 0 ，使得圆 SKIPIF 1 < 0 恒过点 SKIPIF 1 < 0 .
A．①B．②C．③D．④
38．(多选)已知圆x2＋y2－2x＋4y＋3＝0与直线x－y＝1，则（ ）
A．圆心坐标为(1，－2)
B．圆心到直线的距离为 SKIPIF 1 < 0
C．直线与圆相交
D．圆的半径为 SKIPIF 1 < 0
三、填空题
39．圆 SKIPIF 1 < 0 与圆 SKIPIF 1 < 0 内切，则 SKIPIF 1 < 0 的值为______.
40．圆 SKIPIF 1 < 0 关于点 SKIPIF 1 < 0 中心对称的圆的方程为___________.
41．在平面直角坐标系 SKIPIF 1 < 0 中，已知直线 SKIPIF 1 < 0 与x轴交于A点，直线 SKIPIF 1 < 0 与y轴及直线l分别交于B点，C点，且A，B，C，O四点共圆，则此圆的标准方程是__________.
42． SKIPIF 1 < 0 顶点坐标分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．则 SKIPIF 1 < 0 外接圆的标准方程为______．
43．已知半径为3的圆的圆心到y轴的距离等于半径，圆心在直线x-3y＝0上，则此圆的方程为______．
44．写出一个关于直线 SKIPIF 1 < 0 对称的圆的方程___________.
四、解答题
45．如图，已知 SKIPIF 1 < 0 的边 SKIPIF 1 < 0 所在直线的方程为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 边所在直线上且满足 SKIPIF 1 < 0 .
（1）求 SKIPIF 1 < 0 边所在直线的方程；
（2）求 SKIPIF 1 < 0 外接圆的方程；
46．圆C的圆心在x轴上，并且过 SKIPIF 1 < 0 和 SKIPIF 1 < 0 两点，求圆C的方程．
47．已知 SKIPIF 1 < 0 的三个顶点分别是点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的外接圆的标准方程．
48．已知圆 SKIPIF 1 < 0 过点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且圆心在直线 SKIPIF 1 < 0 上．
（1）求圆 SKIPIF 1 < 0 的标准方程；
（2）将圆 SKIPIF 1 < 0 向上平移1个单位长度后得到圆 SKIPIF 1 < 0 ，求圆 SKIPIF 1 < 0 的标准方程．
49．已知抛物线C：x2=−2py经过点（2，−1）．
（Ⅰ）求抛物线C的方程及其准线方程；
（Ⅱ）设O为原点，过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M，N，直线y=−1分别交直线OM，ON于点A和点B.求证：以AB为直径的圆经过y轴上的两个定点．
位置
关系
d与r的
大小关系
图示
点P的坐标特点
点在
圆外
d＞r
(x0－a)2＋(y0－b)2＞r2
点在
圆上
d＝r
(x0－a)2＋(y0－b)2＝r2
点在
圆内
d＜r
(x0－a)2＋(y0－b)2＜r2
标准方程的设法
一般方程的设法
圆心在原点
x2＋y2＝r2
x2＋y2－r2＝0
过原点
(x－a)2＋(y－b)2＝a2＋b2
x2＋y2＋Dx＋Ey＝0
圆心在x轴上
(x－a)2＋y2＝r2
x2＋y2＋Dx＋F＝0
圆心在y轴上
x2＋(y－b)2＝r2
x2＋y2＋Ey＋F＝0
与x轴相切
(x－a)2＋(y－b)2＝b2
x2＋y2＋Dx＋Ey＋eq \f(1,4)D2＝0
与y轴相切
(x－a)2＋(y－b)2＝a2
x2＋y2＋Dx＋Ey＋eq \f(1,4)E2＝0
参考答案：
1．C
【解析】
【分析】
根据三点在坐标系的位置，确定出 SKIPIF 1 < 0 是直角三角形，其中 SKIPIF 1 < 0 是斜边，则有过三点的圆的半径为 SKIPIF 1 < 0 的一半，圆心坐标为 SKIPIF 1 < 0 的中点，进而根据圆的标准方程求解.
【详解】
由已知得， SKIPIF 1 < 0 分别在原点、 SKIPIF 1 < 0 轴、 SKIPIF 1 < 0 轴上，
SKIPIF 1 < 0 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 经过三点圆的半径为 SKIPIF 1 < 0 ，
圆心坐标为 SKIPIF 1 < 0 的中点 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 圆的标准方程为 SKIPIF 1 < 0 .
故选：C.
2．D
【解析】
【分析】
先求得圆 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称的圆的圆心坐标，进而即可得到该圆的方程.
【详解】
圆 SKIPIF 1 < 0 的圆心坐标为 SKIPIF 1 < 0 ，半径为3
设点 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 的对称点为 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，解之得 SKIPIF 1 < 0
则圆 SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称的圆的圆心坐标为 SKIPIF 1 < 0
则该圆的方程为 SKIPIF 1 < 0 ，
故选：D．
3．B
【解析】
【分析】
由题可得 SKIPIF 1 < 0 ，然后利用基本不等式即得.
【详解】
圆 SKIPIF 1 < 0 的圆心为 SKIPIF 1 < 0 ，依题意，点 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，
因此 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时取“=”，
所以 SKIPIF 1 < 0 的最小值为9.
故选：B.
4．C
【解析】
【分析】
由题知，弦 SKIPIF 1 < 0 所在直线方程为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 在弦 SKIPIF 1 < 0 所在直线上，进而得 SKIPIF 1 < 0 .
【详解】
解：因为圆 SKIPIF 1 < 0 与圆 SKIPIF 1 < 0 交于A、B两点，
所以弦 SKIPIF 1 < 0 所在直线方程为 SKIPIF 1 < 0 ，
因为圆 SKIPIF 1 < 0 的圆心为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 平分圆 SKIPIF 1 < 0 的周长，
所以， SKIPIF 1 < 0 在弦 SKIPIF 1 < 0 所在直线上，即 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
故选：C
5．B
【解析】
【分析】
由方程表示圆可构造不等式求得 SKIPIF 1 < 0 的范围，根据推出关系可得结论.
【详解】
若方程 SKIPIF 1 < 0 表示圆，则 SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ；
∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，， SKIPIF 1 < 0 甲是乙的必要不充分条件.
故选：B.
6．B
【解析】
【分析】
由题可知 SKIPIF 1 < 0 ，则可求得 SKIPIF 1 < 0 斜率，进而求得直线方程.
【详解】
由圆方程可知圆心 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，由题可知 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，又MN过点 SKIPIF 1 < 0 ，根据点斜式公式可知直线MN的方程是 SKIPIF 1 < 0 .
故选：B.
7．D
【解析】
【分析】
求出直线l过的定点，再判断此定点与圆C的位置关系即可作答.
【详解】
直线 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 解得 SKIPIF 1 < 0 ，因此，直线 SKIPIF 1 < 0 恒过定点 SKIPIF 1 < 0 ，
又圆 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，显然点A在圆C外，
所以直线 SKIPIF 1 < 0 与圆C可能相离，可能相切，也可能相交，A，B，C都不正确，D正确.
故选：D
8．B
【解析】
【分析】
利用抛物线的定义计算得出 SKIPIF 1 < 0 的值，结合点到圆的位置关系判断可得出结论.
【详解】
抛物线 SKIPIF 1 < 0 的焦点为 SKIPIF 1 < 0 ，准线方程为 SKIPIF 1 < 0 ，圆 SKIPIF 1 < 0 的半径为 SKIPIF 1 < 0 ，圆心 SKIPIF 1 < 0 ，
由抛物线的定义可得 SKIPIF 1 < 0 ，故点 SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 上.
故选：B.
9．B
【解析】
【分析】
根据圆心到直线距离与半径大小比较判断直线与圆位置关系
【详解】
由题意得 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，即直线与圆相切
故选：B
10．D
【解析】
【分析】
根据圆的标准方程，直接进行判断即可.
【详解】
根据圆的标准方程可得，
SKIPIF 1 < 0 的圆心坐标为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，
故选：D.
11．A
【解析】
【分析】
配方得出圆心坐标，代入直线方程求得参数 SKIPIF 1 < 0 值，然后可得圆半径、面积．
【详解】
圆的方程可化为 SKIPIF 1 < 0 ，其圆心为 SKIPIF 1 < 0 .依题意得， SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 圆的半径为 SKIPIF 1 < 0 ，面积为 SKIPIF 1 < 0 ，
故选：A.
12．A
【解析】
【分析】
求出圆心 SKIPIF 1 < 0 的轨迹方程后，根据圆心 SKIPIF 1 < 0 到原点 SKIPIF 1 < 0 的距离减去半径1可得答案.
【详解】
设圆心 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
化简得 SKIPIF 1 < 0 ，
所以圆心 SKIPIF 1 < 0 的轨迹是以 SKIPIF 1 < 0 为圆心，1为半径的圆，
所以 SKIPIF 1 < 0 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 在线段 SKIPIF 1 < 0 上时取得等号，
故选：A.
【点睛】
本题考查了圆的标准方程，属于基础题.
13．B
【解析】
【分析】
根据圆的一般方程所需满足的条件得到不等式，解之即可求出结果.
【详解】
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 .
故选：B.
14．C
【解析】
【分析】
由于点 SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 的外部，所以 SKIPIF 1 < 0 ，从而可求出 SKIPIF 1 < 0 的取值范围
【详解】
解：由题意得 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
故选：C．
15．C
【解析】
【分析】
先设点 SKIPIF 1 < 0 的坐标，再根据两点间距离公式化简条件，解得结果.
【详解】
设点 SKIPIF 1 < 0 的坐标为 SKIPIF 1 < 0 ，
∵ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，动点 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ，两边平方得 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ．
∴ SKIPIF 1 < 0 的轨迹为圆．
故选:C
【点睛】
本题考查动点轨迹方程，考查基本求解能力，属基础题.
16．D
【解析】
【分析】
将 SKIPIF 1 < 0 化为 SKIPIF 1 < 0 ，作出图形，根据 SKIPIF 1 < 0 的几何意义，结合图形和斜率公式可求出结果.
【详解】
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0
所以 SKIPIF 1 < 0
如图，此方程表示的是圆心在原点，半径为1的半圆,

SKIPIF 1 < 0 的几何意义是点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 连线的斜率
如图， SKIPIF 1 < 0 ， SKIPIF 1 < 0
SKIPIF 1 < 0 ， SKIPIF 1 < 0
所以 SKIPIF 1 < 0 的取值范围为 SKIPIF 1 < 0
故选：D
17．D
【解析】
【分析】
配方，由半径的最小值得参数 SKIPIF 1 < 0 值，然后求出圆心到原点距离，再加半径可得.
【详解】
根据题意，圆 SKIPIF 1 < 0 ，
变形可得 SKIPIF 1 < 0 ．
其圆心为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
当圆 SKIPIF 1 < 0 的面积最小时，必有 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 ．
圆 SKIPIF 1 < 0 的方程为 SKIPIF 1 < 0 ，
圆心 SKIPIF 1 < 0 到原点为距离 SKIPIF 1 < 0 ，
则圆上的点到坐标原点的距离的最大值为 SKIPIF 1 < 0 ．
故选：D．
18．A
【解析】
【分析】
根据圆的一般方程表示圆的条件和充分必要条件的判断可得选项.
【详解】
方程 SKIPIF 1 < 0 表示圆需满足 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
所以“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 为圆方程”的充分不必要条件，
故选：A.
【点睛】
本题考查圆的一般方程和充分条件与必要条件的判断，属于基础题.
19．A
【解析】
【分析】
把圆的方程x2＋y2－2x＋2k＋3＝0化为标准型，利用 SKIPIF 1 < 0 ，解出k的取值范围.
【详解】
方程可化为(x－1)2＋y2＝－2k－2，只有－2k－2＞0，即k＜－1时才能表示圆．
故选：A.
20．B
【解析】
【分析】
先配方得圆的标准方程，再根据圆半径最大值时取法得 SKIPIF 1 < 0 的值，最后求直线倾斜角.
【详解】
方程 SKIPIF 1 < 0 可化为 SKIPIF 1 < 0 ，
设圆的半径为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
∴当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得最大值，从而圆的面积最大．
此时，直线方程为 SKIPIF 1 < 0 ，斜率 SKIPIF 1 < 0 ，倾斜角为 SKIPIF 1 < 0 ，
故选：B
【点睛】
本题考查圆的标准方程、直线倾斜角、圆面积最值，考查基本分析求解能力，属基础题.
21．A
【解析】
【分析】
根据二元二次方程表示圆的条件列不等式，由此求得 SKIPIF 1 < 0 的取值范围.
【详解】
由圆的一般式方程可得 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，求得 SKIPIF 1 < 0 ，
故选：A
22．B
【解析】
由方程表示的曲线为圆，可得出关于实数 SKIPIF 1 < 0 的不等式，解出即可.
【详解】
由于方程 SKIPIF 1 < 0 表示的曲线为圆，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 .
因此，实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 .
故选：B.
【点睛】
本题考查利用圆的一般方程求参数，考查计算能力，属于基础题.
23．B
【解析】
根据点 SKIPIF 1 < 0 , SKIPIF 1 < 0 在圆上且关于直线 SKIPIF 1 < 0 对称,可知直线经过圆心.即可求得参数 SKIPIF 1 < 0 的值,配成圆的标准方程即可求得半径.
【详解】
点 SKIPIF 1 < 0 , SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 上 SKIPIF 1 < 0 ,且点 SKIPIF 1 < 0 , SKIPIF 1 < 0 关于直线 SKIPIF 1 < 0 对称
可知直线 SKIPIF 1 < 0 经过圆心
圆心坐标为 SKIPIF 1 < 0
代入直线方程可得 SKIPIF 1 < 0
解得 SKIPIF 1 < 0
所以圆的方程为 SKIPIF 1 < 0
化成标准方程为 SKIPIF 1 < 0
所以圆的半径为 SKIPIF 1 < 0
故选:B
【点睛】
本题考查了直线与圆的位置关系,圆的一般方程与标准方程的转化,属于基础题.
24．D
【解析】
【分析】
根据圆的一般方程，得到圆心和半径，求出面积最小时对应的半径，再求得圆心到坐标原点的距离，进而可求出结果.
【详解】
解：由题意得：
SKIPIF 1 < 0 由 SKIPIF 1 < 0 得 SKIPIF 1 < 0
SKIPIF 1 < 0 圆心为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 时，半径最小，则面积也最小；
SKIPIF 1 < 0 圆心为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 圆心到坐标原点的距离为 SKIPIF 1 < 0 ，
即原点在圆 SKIPIF 1 < 0 外，根据圆的性质，圆上的点到坐标原点的距离的最大值为 SKIPIF 1 < 0 .
故选：D.
25．A
【解析】
【分析】
复数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，表示以 SKIPIF 1 < 0 为圆心，2为半径的圆． SKIPIF 1 < 0 表示圆上的点与点 SKIPIF 1 < 0 的距离，求出 SKIPIF 1 < 0 即可得出．
【详解】
复数 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，表示以 SKIPIF 1 < 0 为圆心，2为半径的圆．
SKIPIF 1 < 0 表示圆上的点与点 SKIPIF 1 < 0 的距离．
SKIPIF 1 < 0 ．
SKIPIF 1 < 0 的最大值是 SKIPIF 1 < 0 ．
故选：A．
【点睛】
本题考查复数的几何意义、圆的方程，求解时注意方程 SKIPIF 1 < 0 表示的圆的半径为2，而不是 SKIPIF 1 < 0 ．
26．A
【解析】
【分析】
根据二元二次方程表示圆的条件求解．
【详解】
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ．
故选：A．
27．D
【解析】
【分析】
根据圆心和半径可直接得到圆的方程.
【详解】
因为圆心为 SKIPIF 1 < 0 ，半径为3，故圆的方程为： SKIPIF 1 < 0 .
故选：D.
【点睛】
本题考查圆的标准方程，一般根据圆心坐标和半径可直接写出圆的标准方程，本题属于基础题.
28．B
【解析】
【分析】
根据点在圆外得 SKIPIF 1 < 0 求解集，应用等价法，由集合的包含关系即可判断条件间的充分、必要关系.
【详解】
将 SKIPIF 1 < 0 化为标准方程，得 SKIPIF 1 < 0
当点 SKIPIF 1 < 0 在圆 SKIPIF 1 < 0 外时，有 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0
∴“ SKIPIF 1 < 0 ”是“点 SKIPIF 1 < 0 ”在圆 SKIPIF 1 < 0 外”的必要不充分条件.
故选：B.
29．D
【解析】
【分析】
化x2+y2﹣kx+2y+k2﹣2＝0为 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 0求得k的范围，然后逐一核对四个选项得答案.
【详解】
由x2+y2﹣kx+2y+k2﹣2＝0，得 SKIPIF 1 < 0 ，
若方程x2+y2﹣kx+2y+k2﹣2＝0表示圆，则 SKIPIF 1 < 0 0，即﹣2＜k＜2.
∴A，B为方程x2+y2﹣kx+2y+k2﹣2＝0表示圆的既不充分也不必要条件，C为充要条件，
而（0，1]⊂（﹣2，2），则D为充分不必要条件.
故选：D.
【点睛】
本题主要考查了圆的一般方程，充分条件，必要条件，属于中档题.
30．D
【解析】
【分析】
求出圆心 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的对称点为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的最小值是 SKIPIF 1 < 0 ．
【详解】
解：圆 SKIPIF 1 < 0 的圆心 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，圆 SKIPIF 1 < 0 ，圆心 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，
圆心 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的对称点为 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 解得 SKIPIF 1 < 0 故 SKIPIF 1 < 0
SKIPIF 1 < 0 ．
故选 SKIPIF 1 < 0 ．
【点睛】
本题考查圆的方程，考查点线对称，考查学生分析解决问题的能力，属于基础题．
31．A
【解析】
利用一般方程表示圆得 SKIPIF 1 < 0 的不等式求解
【详解】
由题 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 解得 SKIPIF 1 < 0
故选：A
【点睛】
本题考查圆的一般方程，是基础题
32．D
【解析】
【分析】
本题目考察圆的一般方程的圆心坐标，以及点到直线的距离公式，通过点到直线的距离公式可以求出参数 SKIPIF 1 < 0 的值，最后是基本不等式中“1”的代入的应用，已知分式为定值，可以求得整式的最小值
【详解】
由题意，知圆心坐标为(1，4)，
圆心到直线 SKIPIF 1 < 0 的距离为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，当且仅当 SKIPIF 1 < 0 SKIPIF 1 < 0 时取“="，即 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 ．
故选：D
33．A
【解析】
【分析】
先化简曲线方程，判断曲线的形状，明确 SKIPIF 1 < 0 的几何意义，结合图像解答.
【详解】
SKIPIF 1 < 0 ， SKIPIF 1 < 0 表示以 SKIPIF 1 < 0 为圆心，3为半径的圆.
SKIPIF 1 < 0 SKIPIF 1 < 0 表示以圆 SKIPIF 1 < 0 上的任意一点 SKIPIF 1 < 0 到 SKIPIF 1 < 0 两点间距离， SKIPIF 1 < 0 的最大值即为 SKIPIF 1 < 0
故选：A
34．A
【解析】
【分析】
先由直线的方程求得直线恒过的定点，再由圆的圆心和半径得出圆的方程得选项.
【详解】
解：因为直线方程为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，所以直线过定点 SKIPIF 1 < 0 ，
所以圆方程为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
故选：A.
35．ACD
【解析】
【分析】
先表示出圆的半径r，可求出r的最大值，即可判断.
【详解】
所给圆的半径为
r＝ SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 ．
所以当m＝－1时，半径r取最大值 SKIPIF 1 < 0 ，此时最大面积是 SKIPIF 1 < 0 ．
故选：ACD
36．CD
【解析】
由题意得点 SKIPIF 1 < 0 在圆外，列出不等式解出 SKIPIF 1 < 0 ，再由二元二次方程表示圆时的特征列出不等式，综合得结果.
【详解】
由题意过点 SKIPIF 1 < 0 有两条直线与圆 SKIPIF 1 < 0 相切，
则点 SKIPIF 1 < 0 在圆外，即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
由方程 SKIPIF 1 < 0 表示圆，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
综上，实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 .
即实数 SKIPIF 1 < 0 取值范围是0， SKIPIF 1 < 0 .
故选：CD.
【点睛】
关键点点睛：
（1）将题意等价转化为点和圆的位置关系；
（2）理解二元二次方程在什么情况下表示圆.
37．AD
【解析】
①根据二次函数 SKIPIF 1 < 0 的对称轴是 SKIPIF 1 < 0 和圆的对称性判断；
②根据二次函数 SKIPIF 1 < 0 交 SKIPIF 1 < 0 轴于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 两点，由 SKIPIF 1 < 0 判断；
③分别令 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，得到A，B，C的坐标代入 SKIPIF 1 < 0 ，得到 SKIPIF 1 < 0 判断；
④由③得到圆M的方程为 SKIPIF 1 < 0 判断；
【详解】
①因为二次函数 SKIPIF 1 < 0 的对称轴是 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 两点关于 SKIPIF 1 < 0 对称，所以圆心 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，故正确；
②因为二次函数 SKIPIF 1 < 0 交 SKIPIF 1 < 0 轴于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 两点，所以 SKIPIF 1 < 0 解得 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，故错误；
③令 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，设圆M的方程为： SKIPIF 1 < 0 ，将A，B，C的坐标代入得： SKIPIF 1 < 0 ，消去 SKIPIF 1 < 0 得 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，因为 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，故错误；
④圆M的方程为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，则圆 SKIPIF 1 < 0 恒过定点 SKIPIF 1 < 0 ，故正确；
故选：AD
【点睛】
本题主要考查二次函数函数的性质以及圆的方程的应用，还考查了运算求解的能力，属于中档题.
38．AD
【解析】
【分析】
根据圆的方程，先求圆心和半径，再依次判断选项.
【详解】
把圆的方程化为标准形式得(x－1)2＋(y＋2)2＝2，所以圆心坐标为(1，－2)，半径为 SKIPIF 1 < 0 ，所以圆心到直线x－y＝1的距离为d＝ SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 ，直线与圆相切．
故选：AD
39． SKIPIF 1 < 0 或 SKIPIF 1 < 0
【解析】
【分析】
首先根据题中圆的标准方程求出圆的圆心与半径，再根据两圆相切求出 SKIPIF 1 < 0 的值为.
【详解】
圆 SKIPIF 1 < 0 的圆心为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，
圆 SKIPIF 1 < 0 的圆心为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，
所以两圆的圆心距 SKIPIF 1 < 0 ，
又因为两圆内切，有 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
【点睛】
本题主要考查了圆的位置关系，根据圆的标准方程求半径与圆心，属于基础题.
40． SKIPIF 1 < 0
【解析】
【分析】
求出圆心的坐标，进而可得出所求圆的标准方程.
【详解】
圆心 SKIPIF 1 < 0 关于点 SKIPIF 1 < 0 中心对称点的坐标为 SKIPIF 1 < 0 ，
故所求圆的方程为 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 .
41． SKIPIF 1 < 0
【解析】
【分析】
由题意得 SKIPIF 1 < 0 为直径，且直线l与m垂直故 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 所以圆心与半径可求，则圆方程易得.
【详解】
由题意A，B，C，O四点共圆且 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，则直线l与m垂直故 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ， SKIPIF 1 < 0
此圆的圆心为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ＝ SKIPIF 1 < 0 ，
所以圆的标准方程为 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0
42． SKIPIF 1 < 0
【解析】
【分析】
设圆的标准方程为 SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 代入计算即可得结果.
【详解】
设圆的标准方程为 SKIPIF 1 < 0 ，因为过点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0
所以 SKIPIF 1 < 0 解得 SKIPIF 1 < 0
则圆的标准方程为 SKIPIF 1 < 0
故答案为： SKIPIF 1 < 0
43． SKIPIF 1 < 0 或 SKIPIF 1 < 0
【解析】
【分析】
设圆的方程为 SKIPIF 1 < 0 ，根据题意列出方程组，求得 SKIPIF 1 < 0 的值，即可求解.
【详解】
由题意，圆的半径为3与 SKIPIF 1 < 0 轴相切，且圆心在直线 SKIPIF 1 < 0 上，
设此圆的方程为 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
所以圆的方程为 SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
故答案为： SKIPIF 1 < 0 或 SKIPIF 1 < 0 .
44． SKIPIF 1 < 0 等，只要圆心在直线上均可.
【解析】
【分析】
设出圆心坐标，利用圆心在直线上可得圆心满足的条件，设圆的半径为1，即可得到答案.
【详解】
设圆心坐标为 SKIPIF 1 < 0 ，
因为圆 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 对称，
所以 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，
则 SKIPIF 1 < 0 ，
取 SKIPIF 1 < 0 ，设圆的半径为1，
则圆的方程 SKIPIF 1 < 0 ，
故答案为： SKIPIF 1 < 0 (不唯一)
45．（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 .
【解析】
【分析】
（1）由 SKIPIF 1 < 0 ，得到 SKIPIF 1 < 0 为 SKIPIF 1 < 0 ，结合直线 SKIPIF 1 < 0 的方程，求得直线 SKIPIF 1 < 0 的斜率，进而求得 SKIPIF 1 < 0 边所在直线的方程；
（2）由（1） SKIPIF 1 < 0 边所在直线的方程为 SKIPIF 1 < 0 ，联立方程组求得 SKIPIF 1 < 0 ，根据 SKIPIF 1 < 0 ，得到 SKIPIF 1 < 0 为 SKIPIF 1 < 0 外接圆的圆心，进而求得圆的标准方程.
【详解】
（1）由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，
又由 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上，所以 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 为 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 边所在直线的方程为 SKIPIF 1 < 0 ，斜率为 SKIPIF 1 < 0 ,
所以直线 SKIPIF 1 < 0 的斜率为 SKIPIF 1 < 0 ，
又因为点 SKIPIF 1 < 0 在直线 SKIPIF 1 < 0 上，所以 SKIPIF 1 < 0 边所在直线的方程为 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 .
（2）由（1） SKIPIF 1 < 0 边所在直线的方程为 SKIPIF 1 < 0 ，
联立方程组 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 为 SKIPIF 1 < 0 斜边上的中点，即为 SKIPIF 1 < 0 外接圆的圆心，
又由 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 外接圆的方程为 SKIPIF 1 < 0 .
46． SKIPIF 1 < 0
【解析】
【分析】
由题意，设圆心坐标和半径表示圆的标准方程，结合待定系数法即可.
【详解】
设圆 SKIPIF 1 < 0 的圆心坐标为 SKIPIF 1 < 0 ，半径为r，
则圆 SKIPIF 1 < 0 的标准方程为： SKIPIF 1 < 0 ，
有 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
所以圆 SKIPIF 1 < 0 的标准方程为： SKIPIF 1 < 0
47． SKIPIF 1 < 0
【解析】
【分析】
由题意可确定圆的直径为 SKIPIF 1 < 0 ，根据中点坐标公式求出圆心坐标，结合两点距离公式求出半径即可.
【详解】
由题意知， SKIPIF 1 < 0 为圆的直径，设圆心为 SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 中点即为 SKIPIF 1 < 0 ，
所以半径为 SKIPIF 1 < 0 ，
故外接圆的标准方程为： SKIPIF 1 < 0 .
48．（1） SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ．
【解析】
【分析】
（1）先求线段 SKIPIF 1 < 0 的垂直平分线，再联立直线 SKIPIF 1 < 0 求解即可；
（2）分析 SKIPIF 1 < 0 向上平移1个单位长度后的圆心和半径即可
【详解】
（1）因为直线 SKIPIF 1 < 0 的斜率为 SKIPIF 1 < 0 ，
所以线段 SKIPIF 1 < 0 的垂直平分线 SKIPIF 1 < 0 的斜率为1．
又易知线段 SKIPIF 1 < 0 的中点坐标为 SKIPIF 1 < 0 ，
所以直线 SKIPIF 1 < 0 的方程为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ．
因为圆心在直线 SKIPIF 1 < 0 上，所以圆心是直线 SKIPIF 1 < 0 与直线 SKIPIF 1 < 0 的交点．
由 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ．
所以圆心为 SKIPIF 1 < 0 ，半径 SKIPIF 1 < 0 ．
所以圆 SKIPIF 1 < 0 的标准方程是 SKIPIF 1 < 0 ．
（2）由（1），知圆 SKIPIF 1 < 0 的圆心坐标为 SKIPIF 1 < 0 ，
将点 SKIPIF 1 < 0 向上平移1个单位长度后得到点 SKIPIF 1 < 0 ，
故圆 SKIPIF 1 < 0 的圆心坐标为 SKIPIF 1 < 0 ，半径为 SKIPIF 1 < 0 ，
故圆 SKIPIF 1 < 0 的标准方程为 SKIPIF 1 < 0 ．
49．(Ⅰ) SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；
(Ⅱ)见解析.
【解析】
【分析】
(Ⅰ)由题意结合点的坐标可得抛物线方程，进一步可得准线方程；
(Ⅱ)联立准线方程和抛物线方程，结合韦达定理可得圆心坐标和圆的半径，从而确定圆的方程，最后令x=0即可证得题中的结论.
【详解】
(Ⅰ)将点 SKIPIF 1 < 0 代入抛物线方程： SKIPIF 1 < 0 可得： SKIPIF 1 < 0 ，
故抛物线方程为： SKIPIF 1 < 0 ，其准线方程为： SKIPIF 1 < 0 .
(Ⅱ)很明显直线 SKIPIF 1 < 0 的斜率存在，焦点坐标为 SKIPIF 1 < 0 ，
设直线方程为 SKIPIF 1 < 0 ，与抛物线方程 SKIPIF 1 < 0 联立可得： SKIPIF 1 < 0 .
故： SKIPIF 1 < 0 .
设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
直线 SKIPIF 1 < 0 的方程为 SKIPIF 1 < 0 ，与 SKIPIF 1 < 0 联立可得： SKIPIF 1 < 0 ，同理可得 SKIPIF 1 < 0 ，
易知以AB为直径的圆的圆心坐标为： SKIPIF 1 < 0 ，圆的半径为： SKIPIF 1 < 0 ，
且： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
则圆的方程为： SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 整理可得： SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ，
即以AB为直径的圆经过y轴上的两个定点 SKIPIF 1 < 0 .
【点睛】
本题主要考查抛物线方程的求解与准线方程的确定，直线与抛物线的位置关系，圆的方程的求解及其应用等知识，意在考查学生的转化能力和计算求解能力.