新高考数学一轮复习考点过关练习 利用导数解决函数的极值问题（含解析）

这是一份新高考数学一轮复习考点过关练习 利用导数解决函数的极值问题（含解析），共34页。

1. 函数的极值
(1)函数极值的定义：如图，函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧f′(x)<0，右侧f′(x)>0. 类似地，函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；而且在点x＝b附近的左侧f′(x)>0，右侧f′(x)<0. 我们把a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值；b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值. 极小值点、极大值点统称为极值点，极小值和极大值统称为极值.
(2)函数在某点取得极值的必要条件和充分条件：一般地，函数y＝f(x)在某一点的导数值为0是函数y＝f(x)在这点取得极值的必要条件. 可导函数y＝f(x)在x＝x0处取极大(小)值的充分条件是：
①f′(x0)＝0；
②在x＝x0附近的左侧f′(x0)>0(<0)，右侧f′(x0)<0(>0).
(3)导数求极值的方法：解方程f′(x)＝0，当f′(x0)＝0时，如果在x0附近的左侧f′(x)>0，右侧f′(x)＜0，那么f(x0)是极大值；如果在x0附近的左侧f′(x)＜0，右侧f′(x)>0，那么f(x0)是极小值.
【题型归纳】
题型一：求已知函数的极值
1．已知函数 SKIPIF 1 < 0 ，则下列说法正确的是（ ）
A．当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极小值1B．当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极大值1
C．当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极大值33D．当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极大值 SKIPIF 1 < 0
2．若函数 SKIPIF 1 < 0 ，给出下面结论：① SKIPIF 1 < 0 为奇函数，② SKIPIF 1 < 0 时有极大值 SKIPIF 1 < 0 ，③ SKIPIF 1 < 0 在 SKIPIF 1 < 0 单调递减，④ SKIPIF 1 < 0 ．其中正确的结论个数（ ）
A．0B．1C．2D．3
3．函数f(x)的导函数为f′(x)＝－x(x＋2)，则函数f(x)有 ( )
A. 最小值f(0) B. 最小值f(－2)
C. 极大值f(0) D. 极大值f(－2)
题型二：根据函数的极值、极值点求参数
4．已知函数 SKIPIF 1 < 0 SKIPIF 1 < 0 有极值，则 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
5．函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 处有极大值 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的值等于（ ）
A．0B．6C．3D．2
6．若函数 SKIPIF 1 < 0 有2个极值点，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
题型三：函数（导函数）图象与极值、极值点的关系
7．函数 SKIPIF 1 < 0 的导函数为 SKIPIF 1 < 0 的图象如图所示，关于函数 SKIPIF 1 < 0 ，下列说法不正确的是（ ）
A．函数在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上单调递增
B．函数在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上单调递减
C．函数存在两个极值点
D．函数有最小值，但是无最大值
8．已知函数 SKIPIF 1 < 0 的导函数 SKIPIF 1 < 0 的图象如图所示，那么（ ）
A．函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上不单调
B．函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的切线的斜率为0
C． SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 的极小值点
D． SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 的极大值点
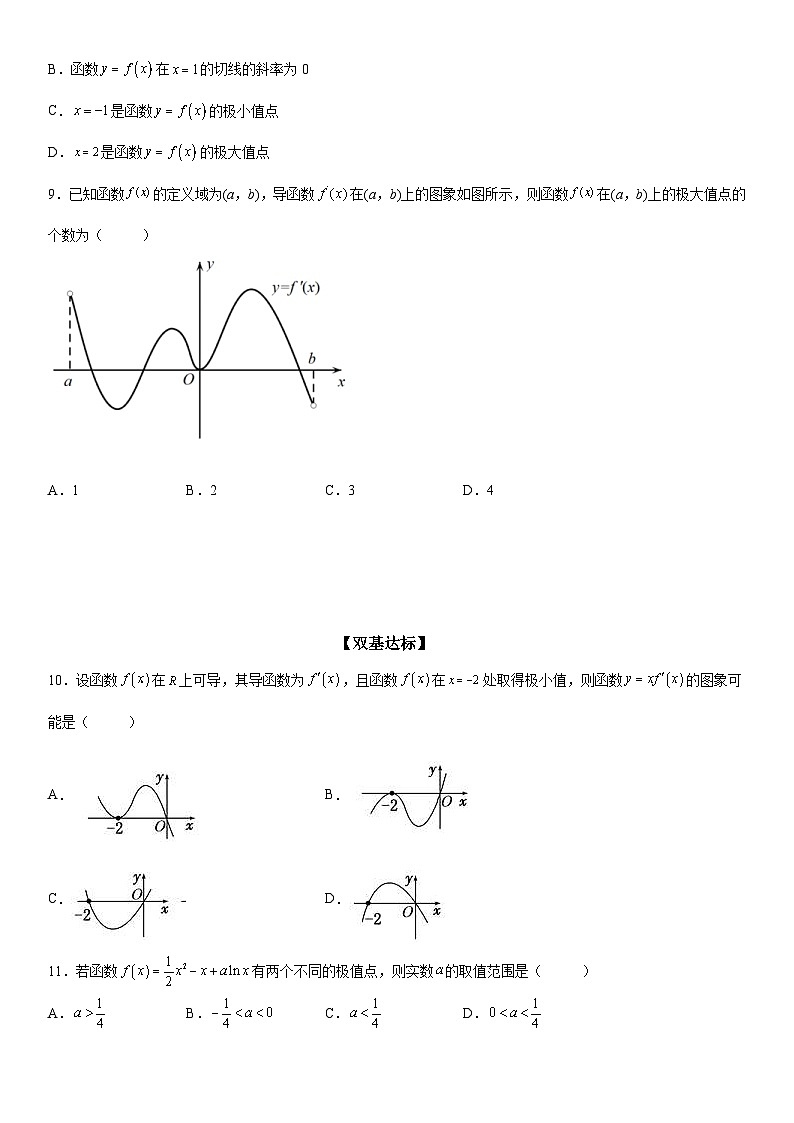
9．已知函数 SKIPIF 1 < 0 的定义域为(a，b)，导函数 SKIPIF 1 < 0 在(a，b)上的图象如图所示，则函数 SKIPIF 1 < 0 在(a，b)上的极大值点的个数为（ ）
A．1B．2C．3D．4
【双基达标】
10．设函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上可导，其导函数为 SKIPIF 1 < 0 ，且函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 处取得极小值，则函数 SKIPIF 1 < 0 的图象可能是（ ）
A．B．
C．D．
11．若函数 SKIPIF 1 < 0 有两个不同的极值点，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
12．已知函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上是增函数，且在 SKIPIF 1 < 0 上仅有一个极大值点，则 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
13．已知函数 SKIPIF 1 < 0 ，则当 SKIPIF 1 < 0 时，函数 SKIPIF 1 < 0 一定有（ ）
A．极大值，且极大值为 SKIPIF 1 < 0 B．极小值，且极小值为 SKIPIF 1 < 0
C．极大值，且极大值为0D．极小值，且极小值为0
14．已知函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 为自然对数的底数），若 SKIPIF 1 < 0 的零点为 SKIPIF 1 < 0 ，极值点为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 （ ）
A． SKIPIF 1 < 0 B．0C．1D．2
15．函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的极大值点为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
16．已知函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，导函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上的图象如图所示，则函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上的极大值点的个数为（ ）
A．4B．3C．2D．1
17．已知函数 SKIPIF 1 < 0 ，则“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 有极值”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
18．已知函数 SKIPIF 1 < 0 ，则（ ）
A． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为增函数B． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上为减函数
C． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有极大值D． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有极小值
19．已知 SKIPIF 1 < 0 在 SKIPIF 1 < 0 处取得极值，则 SKIPIF 1 < 0 的最小值是（ ）
A． SKIPIF 1 < 0 B．2C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
20．已知函数 SKIPIF 1 < 0 有极值，则c的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
21．设函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上可导，其导函数为 SKIPIF 1 < 0 ，且函数 SKIPIF 1 < 0 SKIPIF 1 < 0 的图像如图所示，则下列结论中一定成立的是（ ）
A．函数 SKIPIF 1 < 0 有极大值 SKIPIF 1 < 0 和极小值 SKIPIF 1 < 0
B．函数 SKIPIF 1 < 0 有极大值 SKIPIF 1 < 0 和极小值 SKIPIF 1 < 0
C．函数 SKIPIF 1 < 0 有极大值 SKIPIF 1 < 0 和极小值 SKIPIF 1 < 0
D．函数 SKIPIF 1 < 0 有极大值 SKIPIF 1 < 0 和极小值 SKIPIF 1 < 0
22．已知函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 处取得极值，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 的单调递减区间为 SKIPIF 1 < 0 ；则 SKIPIF 1 < 0 的取值范围为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
23．已知函数 SKIPIF 1 < 0 的导函数为 SKIPIF 1 < 0 ，函数 SKIPIF 1 < 0 的图象如图所示，则下列结论正确的是（ ）
A． SKIPIF 1 < 0 在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上为减函数
B． SKIPIF 1 < 0 在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上为增函数
C． SKIPIF 1 < 0 的极小值为 SKIPIF 1 < 0 ，极大值为 SKIPIF 1 < 0
D． SKIPIF 1 < 0 的极大值为 SKIPIF 1 < 0 ，极小值为 SKIPIF 1 < 0
24．设 SKIPIF 1 < 0 ， SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有3个根，则实数 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
25．若函数 SKIPIF 1 < 0 没有极值，则
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
【高分突破】
单选题
26．若函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上无极值，则实数 SKIPIF 1 < 0 的取值范围（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
27．已知 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
A．在 SKIPIF 1 < 0 上单调递增B．在 SKIPIF 1 < 0 上单调递减
C．有极大值 SKIPIF 1 < 0 ，无极小值D．有极小值 SKIPIF 1 < 0 ，无极大值
28．已知函数 SKIPIF 1 < 0 有极大值和极小值，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
29．已知函数 SKIPIF 1 < 0 有两个不同的极值点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，若不等式 SKIPIF 1 < 0 恒成立，则 SKIPIF 1 < 0 的取值范围是（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
30．函数 SKIPIF 1 < 0 的极值点的个数是（ ）
A．3个B．2个C．1个D．0个
31．若函数 SKIPIF 1 < 0 恰有三个极值点，则 SKIPIF 1 < 0 的取值范围是
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
32．已知函数 SKIPIF 1 < 0 的导函数 SKIPIF 1 < 0 的图像如下，若 SKIPIF 1 < 0 在 SKIPIF 1 < 0 处有极值，则 SKIPIF 1 < 0 的值为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
33．若函数 SKIPIF 1 < 0 的极大值点与极小值点分别为a，b，则（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
34．如图是函数 SKIPIF 1 < 0 的导数 SKIPIF 1 < 0 的图象，则下面判断正确的是（ ）
A．在 SKIPIF 1 < 0 内 SKIPIF 1 < 0 是增函数B．在 SKIPIF 1 < 0 内 SKIPIF 1 < 0 是增函数
C．在 SKIPIF 1 < 0 时 SKIPIF 1 < 0 取得极大值D．在 SKIPIF 1 < 0 时 SKIPIF 1 < 0 取得极小值
二、多选题
35．已知函数 SKIPIF 1 < 0 ，下列结论中正确的是（ ）
A．函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 时，取得极小值-1
B．对于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 恒成立
C．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
D．若 SKIPIF 1 < 0 ，对于 SKIPIF 1 < 0 恒成立，则 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的最小值为1
36．（多选）设 SKIPIF 1 < 0 为函数 SKIPIF 1 < 0 的导函数，已知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则下列结论不正确的是（ ）
A． SKIPIF 1 < 0 在 SKIPIF 1 < 0 单调递增B． SKIPIF 1 < 0 在 SKIPIF 1 < 0 单调递增
C． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有极大值D． SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有极小值
37．已知 SKIPIF 1 < 0 ，下列说法正确的是（ ）
A． SKIPIF 1 < 0 在 SKIPIF 1 < 0 处的切线方程为 SKIPIF 1 < 0 B．单调递增区间为 SKIPIF 1 < 0
C． SKIPIF 1 < 0 的极大值为 SKIPIF 1 < 0 D．方程 SKIPIF 1 < 0 有两个不同的解
38．已知函数 SKIPIF 1 < 0 ，下列说法中正确的有（ ）
A．函数 SKIPIF 1 < 0 的极大值为 SKIPIF 1 < 0 ，极小值为 SKIPIF 1 < 0
B．当 SKIPIF 1 < 0 时，函数 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ，最小值为 SKIPIF 1 < 0
C．函数 SKIPIF 1 < 0 的单调减区间为 SKIPIF 1 < 0
D．曲线 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 处的切线方程为 SKIPIF 1 < 0
三、填空题
39．函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的极值点为______.
40．写出一个存在极值的奇函数______________.
41．若函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上有最大值，则实数 SKIPIF 1 < 0 的取值范围是_________．
42．已知函数 SKIPIF 1 < 0 的一个极值点为1，则 SKIPIF 1 < 0 在[-2，2]上的最小值为_____________．
43．已知函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上存在极值点，则实数a的取值范围是_____________.
44．已知 SKIPIF 1 < 0 和 SKIPIF 1 < 0 分别是函数 SKIPIF 1 < 0 （ SKIPIF 1 < 0 且 SKIPIF 1 < 0 ）的极小值点和极大值点．若 SKIPIF 1 < 0 ，则a的取值范围是____________．
四、解答题
45．已知函数 SKIPIF 1 < 0 .
（1）当 SKIPIF 1 < 0 时，求曲线 SKIPIF 1 < 0 上在点 SKIPIF 1 < 0 处的切线方程；
（2）这下面三个条件中任选一个补充在下面的问题中，并加以解答.若 SKIPIF 1 < 0 ___________，求实数m的取值范围.
①在区间 SKIPIF 1 < 0 上是单调减函数；②在 SKIPIF 1 < 0 上存在减区间；③在区间 SKIPIF 1 < 0 上存在极小值.
46．在① SKIPIF 1 < 0 的一个极值点为0，②若曲线 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 处的切线与直线 SKIPIF 1 < 0 垂直，③ SKIPIF 1 < 0 为奇函数这三个条件中任选一个，补充在下面的问题中，并回答下列问题．
已知函数 SKIPIF 1 < 0 ，且，求 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的最大值与最小值．
注：如果选择多个条件解答，按第一个解答计分．
47．已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
（1）求函数 SKIPIF 1 < 0 的极大值；
（2）求证： SKIPIF 1 < 0 ；
（3）对于函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 定义域上的任意实数 SKIPIF 1 < 0 ，若存在常数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，使得 SKIPIF 1 < 0 和 SKIPIF 1 < 0 都成立，则称直线 SKIPIF 1 < 0 为函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的“分界线”．设函数 SKIPIF 1 < 0 ，试探究函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 是否存在“分界线”？若存在，请加以证明，并求出 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的值；若不存在，请说明理由．
48．已知函数 SKIPIF 1 < 0 ，从① SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 的一个极值点，②函数 SKIPIF 1 < 0 的图象在 SKIPIF 1 < 0 处的切线方程为 SKIPIF 1 < 0 这两个条件中任选一个作为已知条件，并回答下列问题．
（1）求a的值；
（2）求 SKIPIF 1 < 0 的单调区间．
49．已知函数 SKIPIF 1 < 0 ， SKIPIF 1 < 0 .
(1)当 SKIPIF 1 < 0 时，求函数 SKIPIF 1 < 0 的极值；
(2)当 SKIPIF 1 < 0 时，求证： SKIPIF 1 < 0 .
参考答案
1．B
【解析】
【分析】
求导可得 SKIPIF 1 < 0 解析式，令 SKIPIF 1 < 0 ，可得极值点，利用表格法，可得 SKIPIF 1 < 0 的单调区间，代入数据，可得 SKIPIF 1 < 0 的极值，分析即可得答案.
【详解】
由题意得 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
当x变化时， SKIPIF 1 < 0 、 SKIPIF 1 < 0 变化如下
所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极大值1，故B正确、C、D错误，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极小值，故A错误，
故选：B
2．D
【解析】
【分析】
由奇函数的定义即可判断①；求导得出 SKIPIF 1 < 0 时 SKIPIF 1 < 0 的单调性，进而得出极值即可判断②；直接由导数得出 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的单调性即可判断③；利用单调性比较函数值大小即可判断④.
【详解】
易得定义域为 SKIPIF 1 < 0 ，对于①， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 为奇函数，①正确；
对于②，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单增，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单减，则 SKIPIF 1 < 0 时， SKIPIF 1 < 0 有极大值 SKIPIF 1 < 0 ，②正确；
对于③，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单增，③错误；
对于④，由上知， SKIPIF 1 < 0 在 SKIPIF 1 < 0 单调递增，则 SKIPIF 1 < 0 ，又 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，④正确.
则正确的结论有3个.
故选：D.
3．C
【解析】令f′(x)＝－x(x＋2)>0，解得－2令f′(x)＝－x(x＋2)＝0，解得x＝－2或x＝0；
令f′(x)＝－x(x＋2)<0，解得x>0或x<－2，
即函数f(x)的单调递减区间为(－∞，－2)，(0，＋∞).
所以函数f(x)有极大值f(0). 故选C.
4．D
【解析】
【分析】
先求导，由题设得 SKIPIF 1 < 0 必有两个不等的实根，再利用判别式求解即可.
【详解】
由题意知，定义域为R， SKIPIF 1 < 0 ，要使函数 SKIPIF 1 < 0 有极值，则 SKIPIF 1 < 0 必有两个不等的实根，
则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 .
故选：D.
5．A
【解析】
【分析】
求导，根据 SKIPIF 1 < 0 列方程组求解可得.
【详解】
SKIPIF 1 < 0
因为 SKIPIF 1 < 0 在 SKIPIF 1 < 0 处有极大值 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0
所以 SKIPIF 1 < 0
故选：A
6．B
【解析】
【分析】
求导，根据题意可得 SKIPIF 1 < 0 有2个不同的正实数根，从而可得出答案.
【详解】
解： SKIPIF 1 < 0 ，
因为函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，且函数 SKIPIF 1 < 0 有2个极值点，
则 SKIPIF 1 < 0 有2个不同的正实数根，
所以 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，
即实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 .
故选：B．
7．C
【解析】
【分析】
根据导函数的图象判断导函数的正负，从而可求出函数的单调区间和极值
【详解】
由导函数的图象可知，当 SKIPIF 1 < 0 或 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 或 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上单调递增，在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上单调递减，
所以 SKIPIF 1 < 0 和 SKIPIF 1 < 0 为极小值点， SKIPIF 1 < 0 为极大值点，所以函数有3个极值点，
所以 SKIPIF 1 < 0 和 SKIPIF 1 < 0 中的最小的，为函数的最小值，无最大值，
所以ABD正确，C错误，
故选：C
8．D
【解析】
【分析】
根据导函数的图象与原函数的关系逐个判断即可
【详解】
对A，在 SKIPIF 1 < 0 上 SKIPIF 1 < 0 ，故函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调，故A错误；
对B， SKIPIF 1 < 0 ，故函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的切线的斜率大于0，故B错误；
对C， SKIPIF 1 < 0 左右两边都有 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 不是函数 SKIPIF 1 < 0 的极小值点；
对D， SKIPIF 1 < 0 且在 SKIPIF 1 < 0 左侧 SKIPIF 1 < 0 ， SKIPIF 1 < 0 右侧 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 的极大值点，故D正确；
故选：D
9．B
【解析】
【分析】
根据极大值点的定义结合导函数的图象分析判断即可
【详解】
由函数极值的定义和导函数的图象可知， SKIPIF 1 < 0 在(a，b)上与x轴的交点个数为4，但是在原点附近的导数值恒大于零，故x＝0不是函数f(x)的极值点．
其余的3个交点都是极值点，其中有2个点满足其附近的导数值左正右负，
故极大值点有2个．
故选：B
10．C
【解析】
【分析】
根极值与导函数的关系确定 SKIPIF 1 < 0 在 SKIPIF 1 < 0 附近的正负，得 SKIPIF 1 < 0 的正负，从而确定正确选项．
【详解】
由题意可得 SKIPIF 1 < 0 ，而且当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 ，排除B、D；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，此时， SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
所以函数 SKIPIF 1 < 0 的图象可能是C．
故选：C
11．D
【解析】
由 SKIPIF 1 < 0 在 SKIPIF 1 < 0 有2个不同的零点，结合二次函数的性质可求．
【详解】
解：因为 SKIPIF 1 < 0 有两个不同的极值点，
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 有2个不同的零点，
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 有2个不同的零点，
所以 SKIPIF 1 < 0 ，
解可得， SKIPIF 1 < 0 ．
故选： SKIPIF 1 < 0 ．
12．A
【解析】
【分析】
首先根据函数的单调性列出 SKIPIF 1 < 0 ，求出 SKIPIF 1 < 0 ，再由 SKIPIF 1 < 0 在 SKIPIF 1 < 0 SKIPIF 1 < 0 处取得极大值，列出 SKIPIF 1 < 0 ，解不等式即可求解.
【详解】
由题 SKIPIF 1 < 0 ，所以有 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
又因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ；
又 SKIPIF 1 < 0 在 SKIPIF 1 < 0 SKIPIF 1 < 0 处取得极大值，
可得 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
故选：A.
13．A
【解析】
【分析】
根据导数的性质，结合余弦函数的性质、极值的定义进行求解即可.
【详解】
SKIPIF 1 < 0
SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 单调递增，此时 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 单调递减，此时 SKIPIF 1 < 0 ，
所以该函数当 SKIPIF 1 < 0 时，有极大值，没有极小值，
且极大值为 SKIPIF 1 < 0 ，
故选：A
14．C
【解析】
【分析】
令 SKIPIF 1 < 0 可求得其零点，即 SKIPIF 1 < 0 的值，再利用导数可求得其极值点，即 SKIPIF 1 < 0 的值，从而可得答案．
【详解】
解： SKIPIF 1 < 0 ，
SKIPIF 1 < 0 当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 恒成立，
SKIPIF 1 < 0 的零点为 SKIPIF 1 < 0 ．
又当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 为增函数，故在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上无极值点；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
SKIPIF 1 < 0 时， SKIPIF 1 < 0 取到极小值，即 SKIPIF 1 < 0 的极值点 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ．
故选：C．
【点睛】
本题考查利用导数研究函数的极值，考查函数的零点，考查分段函数的应用，突出分析运算能力的考查，属于中档题．
15．D
【解析】
【分析】
求出函数的导数，利用导数确定函数的单调性，即可求出函数的极大值点.
【详解】
SKIPIF 1 < 0 ，
∴当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单调递减，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单调递增，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单调递减，
∴函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的极大值点为 SKIPIF 1 < 0 ．
故选：D
16．B
【解析】
【分析】
通过导函数的图象得到导函数的符号，进而得到原函数的单调性，进而判断出极大值个数.
【详解】
极大值点在导函数 SKIPIF 1 < 0 的零点处，且满足零点的左侧为正，右侧为负，由导函数的图象可知极大值点共有3个.
故选:B.
17．B
【解析】
求导函数，判断导函数的符号，确定有极值时 SKIPIF 1 < 0 的范围即可.
【详解】
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
若 SKIPIF 1 < 0 ， SKIPIF 1 < 0 则 SKIPIF 1 < 0 恒成立，
SKIPIF 1 < 0 为增函数，无极值；
若 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 有两个极值．
所以“ SKIPIF 1 < 0 ”是“ SKIPIF 1 < 0 有极值”的必要不充分条件．
故选:B
18．A
【解析】
【分析】
求导后，令 SKIPIF 1 < 0 ，需要再次求导，从而求得 SKIPIF 1 < 0 的正负，来判断原函数的单调性及极值情况.
【详解】
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，
因此在 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单减；在 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单增；
又 SKIPIF 1 < 0 ，因此 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
故在 SKIPIF 1 < 0 及 SKIPIF 1 < 0 上， SKIPIF 1 < 0 单增， SKIPIF 1 < 0 无极值，
故选：A
【点睛】
关键点点睛：求导后，需要对导数再次求导，从而求得原函数的单调性及极值情况.
19．D
【解析】
求导 SKIPIF 1 < 0 ，根据极值点得到 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，展开利用均值不等式计算得到答案.
【详解】
SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，
根据题意 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
经检验 SKIPIF 1 < 0 在 SKIPIF 1 < 0 处取得极值.
SKIPIF 1 < 0 ，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时，等号成立.
故选： SKIPIF 1 < 0 .
【点睛】
本题考查了根据极值点求参数，均值不等式，意在考查学生的综合应用能力.
20．A
【解析】
【分析】
求导得 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，由此可求答案．
【详解】
解：由题意得 SKIPIF 1 < 0 ，
若函数 SKIPIF 1 < 0 有极值，则 SKIPIF 1 < 0 ，
解得 SKIPIF 1 < 0 ，
故选：A．
21．B
【解析】
【分析】
由函数图象，确定 SKIPIF 1 < 0 的零点并判断 SKIPIF 1 < 0 的区间符号，进而可得 SKIPIF 1 < 0 的单调性，即可知极值情况.
【详解】
由图知：当 SKIPIF 1 < 0 时，有 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 时 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 递增；
SKIPIF 1 < 0 时 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 递减；
SKIPIF 1 < 0 时 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 递增；
SKIPIF 1 < 0 时 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 递增；
综上， SKIPIF 1 < 0 、 SKIPIF 1 < 0 上 SKIPIF 1 < 0 递增； SKIPIF 1 < 0 上 SKIPIF 1 < 0 递减.
∴函数 SKIPIF 1 < 0 有极大值 SKIPIF 1 < 0 和极小值 SKIPIF 1 < 0 .
故选：B
22．D
【解析】
【分析】
求出导函数并根据极值点求得 SKIPIF 1 < 0 的关系，然后用判别式和根与系数的关系讨论导函数的零点问题，最后求出答案.
【详解】
由 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 ，由条件可得 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 可得 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 .
对于方程 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，当且仅当 SKIPIF 1 < 0 时取等号，与 SKIPIF 1 < 0 矛盾，故等号不成立，即 SKIPIF 1 < 0 ，故方程 SKIPIF 1 < 0 有两个实数根： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ，
因为函数的单调递减区间为 SKIPIF 1 < 0 ，容易判断，m=1，于是 SKIPIF 1 < 0 .
故选：D.
23．D
【解析】
根据 SKIPIF 1 < 0 图象，可知该函数的正负性，再结合导数的性质对 SKIPIF 1 < 0 的性质进行判断即可.
【详解】
根据函数 SKIPIF 1 < 0 的图象可知：
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，因此当 SKIPIF 1 < 0 时，函数 SKIPIF 1 < 0 单调递增；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，因此当 SKIPIF 1 < 0 时，函数 SKIPIF 1 < 0 单调递减，显然当 SKIPIF 1 < 0 ，函数有极小值，极小值为 SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，因此当 SKIPIF 1 < 0 时，函数 SKIPIF 1 < 0 单调递减；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，因此当 SKIPIF 1 < 0 时，函数 SKIPIF 1 < 0 单调递增，显然当 SKIPIF 1 < 0 ，函数有极大值，极大值为 SKIPIF 1 < 0 ，
由上可以判断D是正确的.
故选：D
24．A
【解析】
【分析】
由方程 SKIPIF 1 < 0 分离参数并换元成 SKIPIF 1 < 0 ，利用函数 SKIPIF 1 < 0 的图象与直线 SKIPIF 1 < 0 有三个公共点即可得解.
【详解】
由 SKIPIF 1 < 0 得 SKIPIF 1 < 0 ，而 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，于是得 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，于是得 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，在 SKIPIF 1 < 0 上单调递减， SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极大值 SKIPIF 1 < 0 ，
作出函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上的图象及直线 SKIPIF 1 < 0 ，如图，
方程 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有3个根，当且仅当函数 SKIPIF 1 < 0 的图象与直线 SKIPIF 1 < 0 有三个公共点，
观察图象知，函数 SKIPIF 1 < 0 的图象与直线 SKIPIF 1 < 0 有三个公共点，
当且仅当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
所以实数 SKIPIF 1 < 0 的取值范围是 SKIPIF 1 < 0 .
故选：A
25．A
【解析】
【分析】
先求出导函数 SKIPIF 1 < 0 ，然后采用分类讨论的方法分析 SKIPIF 1 < 0 是否有极值，注意定义域的限制.
【详解】
SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .令 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ；令 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 . SKIPIF 1 < 0 在 SKIPIF 1 < 0 处取极小值.
当 SKIPIF 1 < 0 时，方程 SKIPIF 1 < 0 必有一个正数解 SKIPIF 1 < 0 ，
（1）若 SKIPIF 1 < 0 ，此正数解为 SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0 ， SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，无极值.
（2）若 SKIPIF 1 < 0 ，此正数解为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 必有 SKIPIF 1 < 0 个不同的正数解， SKIPIF 1 < 0 存在 SKIPIF 1 < 0 个极值.
综上， SKIPIF 1 < 0 .
故选：A.
【点睛】
本题考查根据函数的极值存在情况求解参数，难度一般.利用导函数分析函数的极值时，要注意到：极值点对应的导函数值一定为零，但是导数值为零的 SKIPIF 1 < 0 值对应的不一定是极值点，因为必须要求在导数值为零处的左右导数值异号.
26．D
【解析】
【分析】
求 SKIPIF 1 < 0 ，由分析可得 SKIPIF 1 < 0 恒成立，利用 SKIPIF 1 < 0 即可求得实数 SKIPIF 1 < 0 的取值范围.
【详解】
由 SKIPIF 1 < 0 可得
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 恒成立， SKIPIF 1 < 0 为开口向上的抛物线，
若函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上无极值，
则 SKIPIF 1 < 0 恒成立，所以 SKIPIF 1 < 0 ，
解得： SKIPIF 1 < 0 ，
所以实数 SKIPIF 1 < 0 的取值范围为 SKIPIF 1 < 0 ，
故选：D.
27．C
【解析】
【分析】
求出导函数 SKIPIF 1 < 0 ，根据导函数的正负，导函数的零点判断各选项．
【详解】
由题意 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 递增， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 递减， SKIPIF 1 < 0 是函数的极大值，也是最大值 SKIPIF 1 < 0 ，函数无极小值．
故选：C．
28．B
【解析】
【分析】
由题，求导函数 SKIPIF 1 < 0 ，由函数有极大值和极小值，即 SKIPIF 1 < 0 有两个不同解，由此 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求解即可
【详解】
由题， SKIPIF 1 < 0 ，函数有极大值和极小值，所以 SKIPIF 1 < 0 有两个不同解，所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
故选：B
29．B
【解析】
【分析】
求得导函数 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，根据极值点可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的表达式及 SKIPIF 1 < 0 的范围，由此可得 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的函数式，构造 SKIPIF 1 < 0 ，则只需 SKIPIF 1 < 0 恒成立，利用导数研究 SKIPIF 1 < 0 的最值，即可求 SKIPIF 1 < 0 的取值范围.
【详解】
由题设， SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 有两个极值点，
∴令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上有两个不等的实根 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 .
又 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 且 SKIPIF 1 < 0 ，要使题设不等式恒成立，只需 SKIPIF 1 < 0 恒成立，
∴ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 递增，故 SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 .
故选：B
【点睛】
关键点点睛：先求导函数，根据极值点、韦达定理求 SKIPIF 1 < 0 ， SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的表达式及 SKIPIF 1 < 0 的范围，再将题设不等式转化为 SKIPIF 1 < 0 恒成立，最后利用导数研究最值求参数范围.
30．C
【解析】
【分析】
对函数求导并求出导函数的零点，再判断导函数在各零点左右的正负即可得解.
【详解】
对函数 SKIPIF 1 < 0 求导得： SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，而当 SKIPIF 1 < 0 和 SKIPIF 1 < 0 时，都有 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以0不是 SKIPIF 1 < 0 的极值点， SKIPIF 1 < 0 是 SKIPIF 1 < 0 的极小值点，函数 SKIPIF 1 < 0 只有一个极值点.
故选：C
31．A
【解析】
【分析】
因为二次函数最多有一个极值点，故先分析 SKIPIF 1 < 0 的部分； SKIPIF 1 < 0 时，令 SKIPIF 1 < 0 ，利用参变分离将 SKIPIF 1 < 0 变形为 SKIPIF 1 < 0 ，构造新函数 SKIPIF 1 < 0 ，判断 SKIPIF 1 < 0 的单调性，得出结论： SKIPIF 1 < 0 最多仅有两解，因此可确定： SKIPIF 1 < 0 时有两个极值点， SKIPIF 1 < 0 时有一个极值点. SKIPIF 1 < 0 时，利用 SKIPIF 1 < 0 与 SKIPIF 1 < 0 有两个交点时(数形结合)，对应求出 SKIPIF 1 < 0 的范围； SKIPIF 1 < 0 时，利用二次函数的对称轴进行分析可求出 SKIPIF 1 < 0 的另一个范围，两者综合即可.
【详解】
由题可知 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时，令 SKIPIF 1 < 0 ，可化为 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，则函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，在 SKIPIF 1 < 0 上单调递减， SKIPIF 1 < 0 的图象如图所示，所以当 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 时， SKIPIF 1 < 0 有两个不同的解；当 SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，综上， SKIPIF 1 < 0 .
【点睛】
分析极值点个数的时候，可转化为导函数为零时方程解的个数问题，这里需要注意：并不是导数值为零就一定是极值点，还需要在该点左右两侧导数值符号相异.
32．B
【解析】
根据极值与导数的关系判断．
【详解】
由 SKIPIF 1 < 0 知， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是极值点．虽然有 SKIPIF 1 < 0 ，但在7的两侧， SKIPIF 1 < 0 ，7不是极值点．
故选：B．
33．C
【解析】
利用导数求函数的极值点，再比较选项.
【详解】
SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 或 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
故 SKIPIF 1 < 0 的极大值点与极小值点分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ．
故选：C
34．B
【解析】
【分析】
根据 SKIPIF 1 < 0 图象判断 SKIPIF 1 < 0 的单调性，由此求得 SKIPIF 1 < 0 的极值点，进而确定正确选项.
【详解】
由图可知， SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上 SKIPIF 1 < 0 递减；在区间 SKIPIF 1 < 0 上 SKIPIF 1 < 0 递增.
所以 SKIPIF 1 < 0 不是 SKIPIF 1 < 0 的极值点， SKIPIF 1 < 0 是 SKIPIF 1 < 0 的极大值点.
所以ACD选项错误，B选项正确.
故选：B
35．BCD
【解析】
【分析】
利用导数研究 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调性及最值即可判断A、B的正误；构造 SKIPIF 1 < 0 ，应用导数研究单调性即知C的正误；构造 SKIPIF 1 < 0 ，应用导数并结合分类讨论的方法研究 SKIPIF 1 < 0 上 SKIPIF 1 < 0 、 SKIPIF 1 < 0 恒成立时m的取值范围，即可判断正误.
【详解】
SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 上 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 上 SKIPIF 1 < 0 递减，则 SKIPIF 1 < 0 ，
∴A错误，B正确；
令 SKIPIF 1 < 0 ，则在 SKIPIF 1 < 0 上 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 递减，
∴ SKIPIF 1 < 0 时，有 SKIPIF 1 < 0 ，C正确；
SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 等价于 SKIPIF 1 < 0 ， SKIPIF 1 < 0 等价于 SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 递增，故 SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 递减，故 SKIPIF 1 < 0 ；
当 SKIPIF 1 < 0 时，存在 SKIPIF 1 < 0 使 SKIPIF 1 < 0 ，
∴此时， SKIPIF 1 < 0 上 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 递增， SKIPIF 1 < 0 ； SKIPIF 1 < 0 上 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 递减，
∴要使 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立，则 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 .
综上， SKIPIF 1 < 0 时， SKIPIF 1 < 0 上 SKIPIF 1 < 0 恒成立， SKIPIF 1 < 0 时 SKIPIF 1 < 0 上 SKIPIF 1 < 0 恒成立，
∴若 SKIPIF 1 < 0 ，对于 SKIPIF 1 < 0 恒成立，则 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的最小值为1，正确.
故选：BCD
【点睛】
关键点点睛：选项D，由题设不等式构造 SKIPIF 1 < 0 ，综合应用分类讨论、导数研究恒成立对应的参数范围，进而判断不等式中参数的最值.
36．AC
【解析】
【分析】
由题意构造函数 SKIPIF 1 < 0 ，利用导数判断 SKIPIF 1 < 0 的单调性和极值情况.
【详解】
由 SKIPIF 1 < 0 可得： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 .
令 SKIPIF 1 < 0 ，则令 SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ；令 SKIPIF 1 < 0 ，解得： SKIPIF 1 < 0 ；
所以函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 单减，在 SKIPIF 1 < 0 单增.
在 SKIPIF 1 < 0 处取得极小值，也是最小值 SKIPIF 1 < 0 ，无极大值.
故选：AC
37．AC
【解析】
对 SKIPIF 1 < 0 求导，结合导数的几何意义可得切线的斜率，再用两点式写出切线方程，可判断选项 SKIPIF 1 < 0 ；利用导数分析函数 SKIPIF 1 < 0 的单调性，极值可判断选项 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；将方程的解个数转化为两个函数图象交点个数，数形结合即可判断选项 SKIPIF 1 < 0 ．
【详解】
解：因为 SKIPIF 1 < 0 ，所以函数的定义域为 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
∴ SKIPIF 1 < 0 的图象在点 SKIPIF 1 < 0 处的切线方程为 SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，故A正确；
在 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单调递增，
在 SKIPIF 1 < 0 上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 单调递减，故B错误，
SKIPIF 1 < 0 的极大值也是最大值为 SKIPIF 1 < 0 ，故C正确；
方程 SKIPIF 1 < 0 的解的个数，即为 SKIPIF 1 < 0 的解的个数，
即为函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 图象交点的个数，
作出函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 图象如图所示：
由图象可知方程 SKIPIF 1 < 0 只有一个解，故D错误.
故选：AC.
38．ACD
【解析】
【分析】
利用导数研究函数 SKIPIF 1 < 0 的极值、最值、单调性，利用导数的几何意义可求得曲线 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 处的切线方程，根据计算结果可得答案.
【详解】
因为 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 ，
由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ，
所以函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上递增，在 SKIPIF 1 < 0 上递减，在 SKIPIF 1 < 0 上递增，故选项 SKIPIF 1 < 0 正确，
所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极大值 SKIPIF 1 < 0 ，
在 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极小值 SKIPIF 1 < 0 ，故选项 SKIPIF 1 < 0 正确，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 为单调递增函数，所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得最小值 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得最大值 SKIPIF 1 < 0 ，故选项 SKIPIF 1 < 0 不正确，
因为 SKIPIF 1 < 0 ，所以曲线 SKIPIF 1 < 0 在点 SKIPIF 1 < 0 处的切线方程为 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，故选项 SKIPIF 1 < 0 正确.
故选：ACD.
【点睛】
本题考查了利用导数求函数的极值、最值、单调区间，考查了导数的几何意义，属于基础题.
39． SKIPIF 1 < 0
【解析】
【分析】
对已知函数求导，研究其在 SKIPIF 1 < 0 上的单调性，即可得出极值点．
【详解】
∵ SKIPIF 1 < 0 ，∴当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 .故极值点为 SKIPIF 1 < 0 .
故答案为 SKIPIF 1 < 0 ．
【点睛】
本题考查利用导数研究极值，是基础题．
40． SKIPIF 1 < 0 （答案不唯一，满足条件即可）
【解析】
【分析】
根据基本初等函数的奇偶性及极值的定义即可求解.
【详解】
根据题意，函数可以为 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极大值, 当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 取得极小值.
又 SKIPIF 1 < 0 ，所以函数是奇函数，
故答案为： SKIPIF 1 < 0 （答案不唯一，满足条件即可．
41． SKIPIF 1 < 0
【解析】
【分析】
由导函数求得极大值，利用极大值点在区间 SKIPIF 1 < 0 上，且 SKIPIF 1 < 0 的极大值可得参数范围．
【详解】
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 或 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 和 SKIPIF 1 < 0 上都递增，在 SKIPIF 1 < 0 上递减，
SKIPIF 1 < 0 ，
SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上有最大值，则 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ．
故答案为： SKIPIF 1 < 0 ．
42．-20
【解析】
【分析】
根据 SKIPIF 1 < 0 ，求出 SKIPIF 1 < 0 ，再利用导数判断函数的单调性，从而求出最值.
【详解】
因为 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ．
因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 在(-2，- SKIPIF 1 < 0 )，(1，2)上单调递增，在（- SKIPIF 1 < 0 ，1）上单调递减．
因为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 在[-2，2]上的最小值为-20．
故答案为：-20
43． SKIPIF 1 < 0 或 SKIPIF 1 < 0
【解析】
计算 SKIPIF 1 < 0 ，然后转化为 SKIPIF 1 < 0 有解，可得 SKIPIF 1 < 0 的范围，最后进行简单检验可得结果.
【详解】
由题可知： SKIPIF 1 < 0 ，
因为函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上存在极值点，所以 SKIPIF 1 < 0 有解
所以 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 或 SKIPIF 1 < 0
当 SKIPIF 1 < 0 或 SKIPIF 1 < 0 时，函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 轴只有一个交点，即 SKIPIF 1 < 0
所以函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 单调递增，没有极值点，故舍去
所以 SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 或 SKIPIF 1 < 0
故答案为： SKIPIF 1 < 0 或 SKIPIF 1 < 0
44． SKIPIF 1 < 0
【解析】
【分析】
由 SKIPIF 1 < 0 分别是函数 SKIPIF 1 < 0 的极小值点和极大值点，可得 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，再分 SKIPIF 1 < 0 和 SKIPIF 1 < 0 两种情况讨论，方程 SKIPIF 1 < 0 的两个根为 SKIPIF 1 < 0 ，即函数 SKIPIF 1 < 0 与函数 SKIPIF 1 < 0 的图象有两个不同的交点，构造函数 SKIPIF 1 < 0 ，利用指数函数的图象和图象变换得到 SKIPIF 1 < 0 的图象，利用导数的几何意义求得过原点的切线的斜率，根据几何意义可得出答案.
【详解】
解： SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 分别是函数 SKIPIF 1 < 0 的极小值点和极大值点，
所以函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 和 SKIPIF 1 < 0 上递减，在 SKIPIF 1 < 0 上递增，
所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，
若 SKIPIF 1 < 0 时，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，则此时 SKIPIF 1 < 0 ，与前面矛盾，
故 SKIPIF 1 < 0 不符合题意，
若 SKIPIF 1 < 0 时，则方程 SKIPIF 1 < 0 的两个根为 SKIPIF 1 < 0 ，
即方程 SKIPIF 1 < 0 的两个根为 SKIPIF 1 < 0 ，
即函数 SKIPIF 1 < 0 与函数 SKIPIF 1 < 0 的图象有两个不同的交点，
∵ SKIPIF 1 < 0 ,∴函数 SKIPIF 1 < 0 的图象是单调递减的指数函数，
又∵ SKIPIF 1 < 0 ,∴ SKIPIF 1 < 0 的图象由指数函数 SKIPIF 1 < 0 向下关于 SKIPIF 1 < 0 轴作对称变换，然后将图象上的每个点的横坐标保持不变，纵坐标伸长或缩短为原来的 SKIPIF 1 < 0 倍得到，如图所示：
设过原点且与函数 SKIPIF 1 < 0 的图象相切的直线的切点为 SKIPIF 1 < 0 ，
则切线的斜率为 SKIPIF 1 < 0 ，
故切线方程为 SKIPIF 1 < 0 ，
则有 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
则切线的斜率为 SKIPIF 1 < 0 ，
因为函数 SKIPIF 1 < 0 与函数 SKIPIF 1 < 0 的图象有两个不同的交点，
所以 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ，
又 SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
综上所述， SKIPIF 1 < 0 的范围为 SKIPIF 1 < 0 .
【点睛】
本题考查了函数的极值点问题，考查了导数的几何意义，考查了转化思想及分类讨论思想，有一定的难度.
45．（1） SKIPIF 1 < 0 ；
（2）若选①： SKIPIF 1 < 0 ；若选②： SKIPIF 1 < 0 ；若选③： SKIPIF 1 < 0 .
【解析】
【分析】
（1）求得 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，进而可得切线方程；
（2）若选①，则转化为 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上恒成立，根据“三个二次”可得结果；
若选②，则转化为 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上有解，分离变量可得结果；
若选③，求得 SKIPIF 1 < 0 的极小值点为 SKIPIF 1 < 0 ，解不等式 SKIPIF 1 < 0 可得结果.
【详解】
（1）当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，所以 SKIPIF 1 < 0 ，
点 SKIPIF 1 < 0 为切点， SKIPIF 1 < 0 ，
函数在点 SKIPIF 1 < 0 处的切线方程为： SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ；
（2）∵ SKIPIF 1 < 0 ，
∴若选①：函数 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上是单调减函数，则有：
SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上恒成立，即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立，
∴ SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ；
若选②：函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上存在减区间，则有 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上有解，
即得 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上有解，
此时令 SKIPIF 1 < 0 ，显然 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上单调递减，
所以 SKIPIF 1 < 0 ，故有 SKIPIF 1 < 0 ；
若选③：函数在区间 SKIPIF 1 < 0 上存在极小值，则函数 SKIPIF 1 < 0 的极小值点应落在 SKIPIF 1 < 0 内.
令 SKIPIF 1 < 0 ，求得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，
此时可得， SKIPIF 1 < 0 在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上单调递增；在 SKIPIF 1 < 0 上单调递减；
所以 SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 的极小值点，
即得 SKIPIF 1 < 0 ，
当 SKIPIF 1 < 0 时，不等式恒成立，
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，解之可得 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 .
46．选择性条件见解析， SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ，最小值为0
【解析】
【分析】
若选①，根据导数和函数极值的关系求出 SKIPIF 1 < 0 的值，再根据导数与函数最值的关系即可求出最值；
若选②，先利用导数的几何意义求出 SKIPIF 1 < 0 的值，再根据导数与函数最值的关系即可求出最值；
若选③，先根据奇函数的性质求出 SKIPIF 1 < 0 的值，再根据导数与函数最值的关系即可求出最值；
【详解】
解：选择①，因为 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ．得 SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，在 SKIPIF 1 < 0 上单调递增，
所以 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 ．
因为 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ．
选择②，因为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，在 SKIPIF 1 < 0 上单调递增，
所以 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 ．
因为 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ．
选择③，因为 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 ，
因为 SKIPIF 1 < 0 为奇函数，
所以由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ．
SKIPIF 1 < 0 ，令 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ．
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，在 SKIPIF 1 < 0 上单调递增，
所以 SKIPIF 1 < 0 的最小值为 SKIPIF 1 < 0 ．
因为 SKIPIF 1 < 0 ．
所以 SKIPIF 1 < 0 的最大值为 SKIPIF 1 < 0 ．
【点睛】
此题考查导数和函数的最值的关系，以及导数与函数极值，曲线的切线方程，函数的奇偶性，属于中档题
47．（1） SKIPIF 1 < 0 （2）证明见解析 （3）存在 SKIPIF 1 < 0
【解析】
【分析】
（1）求出函数 SKIPIF 1 < 0 得到函数大单调性，从而得到函数的极大值.
（2）由（1）可得 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，然后可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 SKIPIF 1 < 0 ，相加可证明.
(3) SKIPIF 1 < 0 与 SKIPIF 1 < 0 的图象在 SKIPIF 1 < 0 处有公共点 SKIPIF 1 < 0 ,设函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 存在“分界线” SKIPIF 1 < 0 ,由令 SKIPIF 1 < 0 ，由 SKIPIF 1 < 0 求出参数 SKIPIF 1 < 0 的值，再证明 SKIPIF 1 < 0 成立即可.
【详解】
（1） SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
由 SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，可得 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，在 SKIPIF 1 < 0 上单调递减.
所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 有极大值 SKIPIF 1 < 0
（2）由（1）可知， SKIPIF 1 < 0 为 SKIPIF 1 < 0 的最大值，即 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 （当且仅当 SKIPIF 1 < 0 时等号成立）
令 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，取 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0
则 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 SKIPIF 1 < 0
由上面不等式相加得 SKIPIF 1 < 0
即 SKIPIF 1 < 0
即 SKIPIF 1 < 0
（3）设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递减，在 SKIPIF 1 < 0 上单调递增.
所以 SKIPIF 1 < 0
即 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的图象在 SKIPIF 1 < 0 处有公共点 SKIPIF 1 < 0
设函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 存在“分界线” SKIPIF 1 < 0
令 SKIPIF 1 < 0
由 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立，
即 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上恒成立，
SKIPIF 1 < 0 成立，而 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
再证明 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 恒成立.
设 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时， SKIPIF 1 < 0
所以 SKIPIF 1 < 0 在 SKIPIF 1 < 0 上单调递增，在 SKIPIF 1 < 0 上单调递减.
所以当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 有最大值，即 SKIPIF 1 < 0
所以 SKIPIF 1 < 0 恒成立.
综上所述，可得 SKIPIF 1 < 0 且 SKIPIF 1 < 0
故函数 SKIPIF 1 < 0 与 SKIPIF 1 < 0 存在 “分界线” SKIPIF 1 < 0 ，此时 SKIPIF 1 < 0
【点睛】
本题考查利用导数求函数的极值，利用导数证明不等式，考查恒成立求参数，考查转化思想的应用，属于难题.
48．（1）条件性选择见解析， SKIPIF 1 < 0 ；（2）单调递减区间为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，单调递增区间为 SKIPIF 1 < 0 ．
【解析】
【分析】
（1）选①，求出函数的导函数，根据 SKIPIF 1 < 0 是函数 SKIPIF 1 < 0 的一个极值点，得函数在 SKIPIF 1 < 0 处得到函数值为0，即可得出答案；
选②，根据函数 SKIPIF 1 < 0 的图象在 SKIPIF 1 < 0 处的切线方程为 SKIPIF 1 < 0 ，即函数在 SKIPIF 1 < 0 处得导数值为3，即可的解；
（2）由（1）得 SKIPIF 1 < 0 ，求出函数得导函数，再根据导函数得符号即可得出答案.
【详解】
解：（1）选①．
由题意知， SKIPIF 1 < 0 ，
依题意得， SKIPIF 1 < 0 ，
即 SKIPIF 1 < 0 ，经检验 SKIPIF 1 < 0 符合题意．
选②．
由题意知， SKIPIF 1 < 0 ，
因为函数 SKIPIF 1 < 0 的图象在 SKIPIF 1 < 0 处的切线方程为 SKIPIF 1 < 0 ，
所以 SKIPIF 1 < 0 ，得 SKIPIF 1 < 0 ．
（2）由（1）得 SKIPIF 1 < 0 ，
SKIPIF 1 < 0 ，
令 SKIPIF 1 < 0 得， SKIPIF 1 < 0 或 SKIPIF 1 < 0 ，
列表：
所以 SKIPIF 1 < 0 的单调递减区间为 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，单调递增区间为 SKIPIF 1 < 0 ．
49．(1)有极小值 SKIPIF 1 < 0 ，无极大值
(2)证明见解析
【解析】
【分析】
（1）求函数的导数，结合函数极值和单调性的关系进行求解即可；
（2）当 SKIPIF 1 < 0 时，利用零点的存在性定理可得函数 SKIPIF 1 < 0 存在零点，结合函数极值和导数之间的关系求最值，利用基本不等式法进行证明即可.
(1)
函数 SKIPIF 1 < 0 的定义域为 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时 SKIPIF 1 < 0 ，
函数的导数为 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0
又 SKIPIF 1 < 0 ，故 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上单调递增，
则当 SKIPIF 1 < 0 时 SKIPIF 1 < 0 ，当 SKIPIF 1 < 0 时 SKIPIF 1 < 0 ，
所以函数 SKIPIF 1 < 0 在 SKIPIF 1 < 0 单调递减，在 SKIPIF 1 < 0 单调递增，
所以函数在 SKIPIF 1 < 0 时有极小值 SKIPIF 1 < 0 ，无极大值
(2)
当 SKIPIF 1 < 0 时， SKIPIF 1 < 0
故 SKIPIF 1 < 0 在区间 SKIPIF 1 < 0 上单调递增，其中 SKIPIF 1 < 0
且当 SKIPIF 1 < 0 上时， SKIPIF 1 < 0 ，取 SKIPIF 1 < 0
则有 SKIPIF 1 < 0
故导函数 SKIPIF 1 < 0 存在零点 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 为极小值点，
满足 SKIPIF 1 < 0 ，
故 SKIPIF 1 < 0 (当且仅当 SKIPIF 1 < 0 即 SKIPIF 1 < 0 时取等号)，
即 SKIPIF 1 < 0
x
SKIPIF 1 < 0
-1
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
+
0
-
0
+
SKIPIF 1 < 0
SKIPIF 1 < 0
极大值
SKIPIF 1 < 0
极小值
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
-1
SKIPIF 1 < 0
3
SKIPIF 1 < 0
SKIPIF 1 < 0
-
0
+
0
-
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0
SKIPIF 1 < 0