辽宁省鞍山市铁西区2023-2024学年七年级下学期开学考试数学试题（原卷版+解析版）

这是一份辽宁省鞍山市铁西区2023-2024学年七年级下学期开学考试数学试题（原卷版+解析版），文件包含辽宁省鞍山市铁西区2023-2024学年七年级下学期开学考试数学试题原卷版docx、辽宁省鞍山市铁西区2023-2024学年七年级下学期开学考试数学试题解析版docx等2份试卷配套教学资源，其中试卷共21页， 欢迎下载使用。

温馨提示：请每一位考生把所有的答案都答在答题卡上，否则不给分，答题要求见答题卡．
一．选择题：（2分*10＝20分）
1. 小明为了了解本地气温变化情况，记录了某日时的气温是℃，时的气温升高了2℃，到晚上时气温又降低了6℃，则时的气温为（ ）
A. 6℃B. －8℃C. ℃D. ℃
【答案】B
【解析】
【分析】本题考查了有理数的加减法运算．熟练掌握有理数的加减法运算是解题的关键．
先根据气温上升用加下降用减列出算式，然后利用运算法则进行计算．
【详解】解：℃．
故选B．
2. 由6个小正方体分别搭成立体图形，如图所示，从（ ）看它们的形状是完全相同的．
A. 正面B. 左面C. 后面D. 上面
【答案】B
【解析】
【分析】本题考查了从不同方向看立体图形．根据从不同方向看几何体即可得到结论．
【详解】解：如图所示，从左面看它们的形状是完全相同的．
故选：B．
3. 若．则的值为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查绝对值得非负性，代入求值，根据绝对值得非负性得到，，然后求出x，y的值，代入即可解题．
【详解】解：∵，
∴，，
解得，，
∴，
故选C．
4. 已知单项式与和为单项式，则等于（ ）
A. B. C. 16D. 9
【答案】A
【解析】
【分析】本题考查整式的加减，同类项，乘方．
根据单项式与和为单项式，得到与是同类项，进而根据同类项的定义进行求解．
【详解】解：∵单项式与和为单项式，
∴单项式与是同类项，
∴，，
∴，
∴．
故选：A
5. 下面四个整式中，不能表示图中阴影部分面积的是（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查列代数式，根据不同的方法表示出阴影部分的面积即可．
【详解】解：A、三个阴影部分的面积分别为、、，所以阴影部分面积为，故该选项符合题意；
B、上半部分阴影面积为：，下半部分阴影面积为：，所以阴影部分面积为：，故该选项不符合题意；
C、左半部分阴影面积为：，右半部分阴影面积为：，所以阴影部分面积为：，故该选项不符合题意；
D、大长方形面积：，空白处小长方形面积：，所以阴影部分面积：，故该选项不符合题意；
故选：A．
6. 解方程时，去分母后可以得到（ ）
A. 1﹣x﹣3=3xB. 6﹣2x﹣6=3xC. 6﹣x+3=3xD. 1﹣x+3=3x
【答案】B
【解析】
【分析】
【详解】方程两边都乘以6得： 6-2x-6=3x ，
故选B
【点睛】本题主要考查了一元一次方程的解法，解一元一次方程的基本步骤是：①去分母；②去括号；③移项；④合并同类项；⑤系数化为1；在解方程的过程中要注意以下的问题：①去分母时要把方程两边的每一项都乘以最简公分母，不要漏乘；②去括号时括号前是负号，去括号后括号内的每一项都要改变符号.
7. 我国古代数学著作《孙子算经》中有如下问题：“今有三人共车，二车空；二人共车，九人步，问人与车各几何？”其意思是：“每车坐3人，空出来2车；每车坐2人，9人没车坐．问人数与车数各为多少？”设有个人，根据题意，可列出方程（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了一元一次方程的应用，根据题意，找到等量关系，列出方程是解题的关键．根据车辆数不变，即可列出方程．
【详解】每车坐3人，空出来2车，
车辆数为，
每车坐2人，9人没车坐，
车辆数为，
根据题意得．
故选：C．
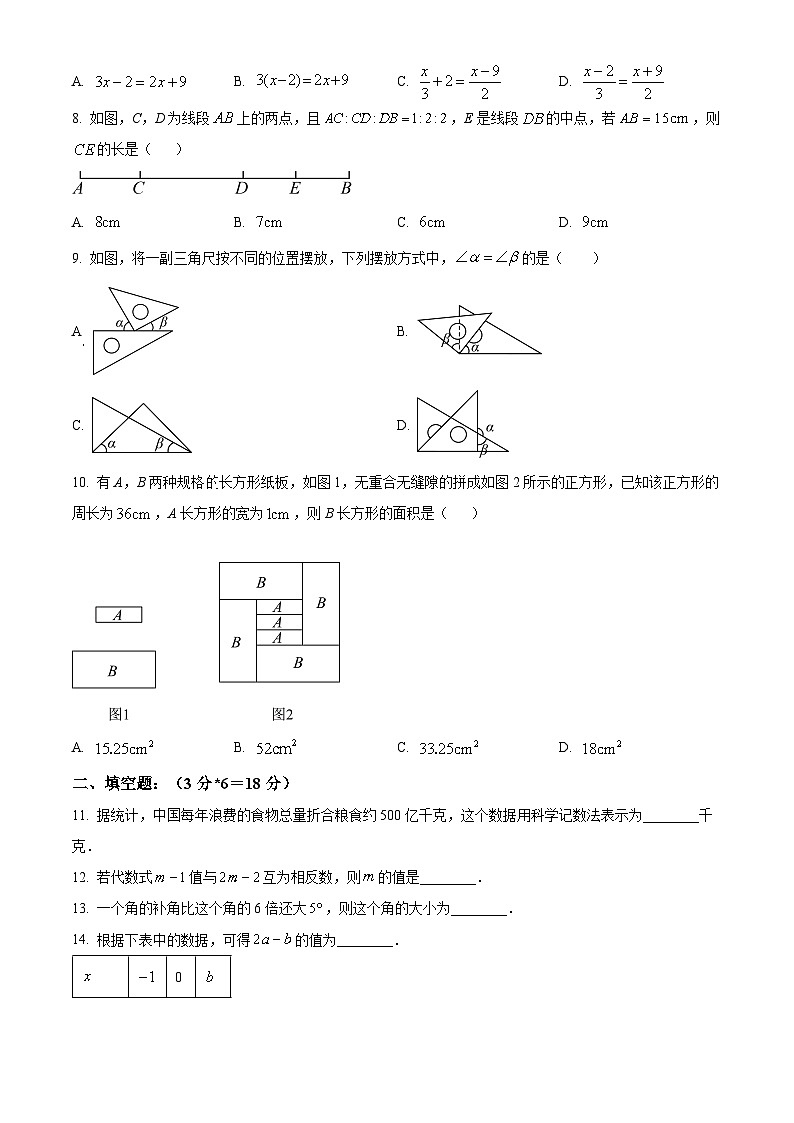
8. 如图，C，D为线段上的两点，且，E是线段的中点，若，则的长是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查线段的和差，线段的中点．
根据，可得到，，由点E是线段的中点，可求得，进而根据即可求解．
【详解】解：∵，，
∴，，，
∵点E是线段的中点，
∴，
∴．
故选：D
9. 如图，将一副三角尺按不同的位置摆放，下列摆放方式中，的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】本题主要考查了余角和补角，需结合余角和补角定义进行求解；
如果两个角的和是，那么称这两个角互为余角，简称互余，也可以说其中一个角是另一个角的余角．如果两个角的和是，那么称这两个角互为补角，简称互补，也可以说其中一个角是另一个角的补角；根据图象求解即可．
【详解】解：A．由图可知，所以与互余，故本选项错误；
B．同角的余角相等，所以，故本选项正确；
C．由图可知，但推不出，故本选项错误；
D．由图可知，所以和互补，故本选项错误．
故选：B．
10. 有A，B两种规格的长方形纸板，如图1，无重合无缝隙的拼成如图2所示的正方形，已知该正方形的周长为，A长方形的宽为，则B长方形的面积是（ ）

A. B. C. D.
【答案】D
【解析】
【分析】本题考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．
设长方形的宽是，则长方形的长是，大正方形的边长为，根据大正方形周长为，列出方程求解即可．
【详解】解：设长方形的宽是，则长方形的长是，大正方形的边长为，
该正方形周长为6，
，
解得：．
长方形的宽是，则长方形的长是，
B长方形的面积：．
故选：D．
二、填空题：（3分*6＝18分）
11. 据统计，中国每年浪费的食物总量折合粮食约500亿千克，这个数据用科学记数法表示为________千克．
【答案】
【解析】
【分析】本题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．
根据科学记数法的表示方法表示即可．
【详解】解：500亿，
故答案为：．
12. 若代数式值与互为相反数，则的值是________．
【答案】1
【解析】
【分析】本题考查互为相反数的定义、解一元一次方程，根据互为相反数的定义列出方程并求解是解题的关键．根据互为相反数的定义得到关于m的方程，解方程即可求得m的值．
【详解】解：根据题意：，即，
解得：，
故答案为：1．
13. 一个角补角比这个角的6倍还大，则这个角的大小为________．
【答案】##25度
【解析】
【分析】本题考查了补角的有关计算，一元一次方程的应用，表示出这个角的余角与补角，然后列出方程是解题的关键．
设这个角的度数为，根据题意列方程进行求解即可．
【详解】解：设这个角的度数为，
根据题意，得，
解得：，
所以这个角的度数为．
故答案为：．
14. 根据下表中的数据，可得的值为________．
【答案】##
【解析】
【分析】本题考查代数式求值．根据表格的数据可先求出a，b，再代入计算即可．
【详解】解：根据表格可知：当时，；
当时，，则；
，
故答案为：．
15. 如图，将一副三角板摆成如图形状，如果，那么的度数是________．

【答案】##度
【解析】
【分析】本题考查三角板中角度的计算．正确的识图，理清角的和差关系是解题的关键．
利用即可求解．
【详解】解：由图可知：，
，
，
．
故答案为：．
16. 数学活动课上对依次排列的两个整式，按如下规则进行操作，每次操作增加的项，都是用上一次操作得到的最末项减去其前一项的差，将这个活动命名为“逆差”游戏．
第1次操作后得到整式：，，；
第2次操作后得到整式：，，，；
……
则该游戏第200次操作后得到的整式串各项之和是________．
【答案】
【解析】
【分析】此题考查了整式的加减，找到结果的规律即可进行解答．
【详解】解：第1次操作后得到整式：，，；则
第2次操作后得到整式：，，，；则
第3次操作后得到整式：，，，，；则
第4次操作后得到整式：，，，，，；则
第5次操作后得到整式：，，，，，，；则
第6次操作后得到整式：，，，，，，，；则
第7次操作后得到整式：，，，，，，，，；则
……
经过7次操作后，发现结果按照，，，0，，，循环出现，
∵，
∴该游戏第200次操作后得到的整式串各项之和与第2次操作的结果相同，即为，
故答案为：
三、解答题：（3个小题，17题16分，18题4分，19题5分共25分）
17. （1）计算：；
（2）计算：；
（3）解方程：；
（4）解方程：
【答案】（1）；（2）；（3）；（4）；
【解析】
【分析】本题主要考查有理数的混合运算，解一元一次方程．
（1）先将除法转为乘法，计算乘法，再利用乘法运算律简便计算即可；
（2）先算乘方，除法转为乘法，再算乘法，最后算减法即可；
（3）根据去括号，移项，合并同类项，系数化为1求解即可；
（4）根据去分母，去括号，移项，合并同类项，系数化为1求解即可．
【详解】解：（1）原式
；
（2）原式
；
（3）
；
（4）
．
18. 某商店在甲批发市场以每包元的价格进了30包茶叶，又在乙批发市场以每包元的价格进了同样的70包茶叶，如果商家以每包元的价格卖出这种茶叶，全部卖完后，请你通过计算说明这家商店的盈亏情况．
【答案】盈利元
【解析】
【分析】此题考查了列代数式，整式加减运算的应用，解题的关键是读懂题意．
根据题意列出商店在甲批发市场茶叶的利润，以及商店在乙批发市场茶叶的利润，将两利润相加表示出总利润，根据大于判断出其结果大于0，可得出这家商店盈利了，从而得出这家商店盈利的总利润．
【详解】解：根据题意可得：
在甲批发市场购买茶叶的利润为：元，
在乙批发市场购买茶叶的利润为：元，
∴卖完后该商店的总利润为：元，
，
∴20a-20b>0，
∴该商店盈利了，盈利元．
19. 如图，数轴上A点所表示的数是，B点所表示的数是3，C为数轴上的一点，且，D为线段的中点，求D点表示的数．
【答案】2或0
【解析】
【分析】本题考查了有理数与数轴，线段中点的定义等知识，分点C在点A的左侧和点C在点A的右侧两种情况求解即可．
【详解】解：∵数轴上A点所表示的数是，B点所表示的数是3，
∴，
当C在A左边时，
∵，，
∴，
∵D为中点，
∴，
∴D点表示的数为0；
当C在A右边，
∵，，
∴，
∵D为中点，
∴，
∴D点表示的数为2
∴D点表示的数为2或0．
四、解答题：（2个小题，20题9分，21题9分，共18分）
20. 如图，在长方形中，，．动点P从点A出发，沿线段向点C运动，速度为；动点Q从点B出发，沿线段BC向点C运动，速度为．点P、Q同时出发，任意一点到达点C时两点同时停止运动．设运动时间为t（s）．

（1）点P，Q同时出发，求几秒后P，Q两点相遇？
（2）求停止运动时P，Q两点之间的距离．
【答案】（1）P，Q出发4秒相遇
（2）P，Q两点之间的距离为
【解析】
【分析】本题考查一元一次方程的应用．
（1）根据追及问题列方程求解即可；
（2）先求得动点P到达点C时所用的时间，据此计算即可求解．
【小问1详解】
解：由题意得，
解得，
答：P，Q出发4秒相遇；
【小问2详解】
解：动点P到达点C时用时：，
，
，
答：P，Q两点之间的距离为．
21. 对于一个任意三位数A，将其个位数字与十位数字对调得到B，则称B为A的“关联数”，将一个数与它的“关联数”的差的绝对值与9的商记为，例如523为532的“关联数”，．
（1） ；
（2）对于一个任意三位数A，百位数字为，十位数字为，个位数字为，，求．
【答案】（1）3 （2）
【解析】
【分析】本题主要考查整式的加减，定义新运算．解题的关键是读懂题意，能够正确的用字母表示三位数．
（1）根据题意，仿照例题即可求出的值；
（2）根据题意，先列出的式子，再进行化简即可．
【小问1详解】
解：；
【小问2详解】
解：∵这个三位数A，百位数字为，十位数字为，个位数字为，
∴这个三位数A是，A的“关联数”是，
∵，
∴．
五、解答题：（2个小题，22题9分，23题10分，共19分）
22. 在一次数学实践探究活动中，小明和他的同伴们将一个直角三角尺按如图所示方式放置，发现了其中的奥秘．
（1）如图①，三角尺的直角顶点P在直线上，点A，B在直线的同侧．若，求度数．
（2）绕点P旋转三角尺，使点A，B在直线的同侧，如图②，若平分，平分，他们发现的度数为定值，请你求出这个定值．
（3）绕点P旋转三角尺，使点A，B在直线的异侧，平分，平分，设，如图③，探究的度数．
【答案】（1）
（2）
（3）
【解析】
【分析】本题考查角的和差，角平分线的定义．
（1）根据即可求解；
（2）由可得到，根据角平分线的定义，可得，进而根据角的和差即可求解；
（3）由，求得，，根据角平分线的定义可得，，最后根据即可求解．
【小问1详解】
解：，
；
【小问2详解】
解：∵，
∴，
平分，平分，
，
，
；
【小问3详解】
解：∵，，
∴，
∴，
∵平分，
∴，
∵平分，
∴，
．
23. 综合与实践
问题情境：
要开学了，小丽和同学们在周末相约去文具店买文具，下表为该文具店促销海报
小丽记录了大家的购买情况，并根据要求一次买好，已知他们共要买7个文具袋，x支钢笔和3支自动铅笔，单买钢笔和自动铅笔单价比组合购买单价要多，并且每人都买1个文具袋，最多买1支钢笔，1支自动铅笔．
数学思考：
（1）他们共买了 份B组合．（用含x的代数式表示）
问题解决：
（2）若他们所买的组合中共有5支钢笔，求他们实际消费的金额．
（3）若他们优惠后共花费240元，请求出他们的组合是如何搭配的．
【答案】（1）；（2）232元；（3）他们是这样搭配的：1份A组合，3份B组合，3份C组合
【解析】
【分析】本题考查了一元一次方程的应用，列代数式，根据各数量之间的关系，正确列出一共的花费是解题的关键．
（1）由三种组合中均包含文具袋且只有C组合中含自动铅笔，即可得出他们购买B组合的数量；
（2）由三种组合中均包含钢笔且只有C组合中含自动铅笔，即可得出他们购买了份C组合，进一步得到A组合数量，即可得出一共的花费；
（3）由题意可得C组合购买份，B组合共x份，A组合份，再根据花费240元，然后列出方程求解即可．
【详解】（1）他们共买了份B组合，
故答案为：；
（2）元
（3）∵，
∴总价格不超过300元，
，
x=6
∴他们是这样搭配的：1份A组合，3份B组合，3份C组合．
0
种类
组合
价格/元
优惠活动
A组合
1个文具袋
30
消费满150元，减24元；消费满300元，减48元………依此类推
B组合
1个文具袋＋1支钢笔
38
C组合
1个文具袋＋1支钢笔＋1支自动铅笔
40