



新高考数学一轮复习讲与练第19讲 空间点、直线、平面之间的位置关系(练)(2份打包,原卷版+解析版)
展开1.如图所示,直三棱柱 SKIPIF 1 < 0 中, SKIPIF 1 < 0 分别是 SKIPIF 1 < 0 的中点, SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角的余弦值为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.下列能保证直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 平行的条件是( )
A. SKIPIF 1 < 0 , SKIPIF 1 < 0
B. SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0
C. SKIPIF 1 < 0 、 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,且 SKIPIF 1 < 0
D. SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0
3.在三棱锥 SKIPIF 1 < 0 中 SKIPIF 1 < 0 分别是 SKIPIF 1 < 0 边的中点,且 SKIPIF 1 < 0 ,则四边形 SKIPIF 1 < 0 是( )
A.平行四边形B.矩形C.菱形D.正方形
4.对于直线m、n和平面 SKIPIF 1 < 0 ,下面命题中的真命题是( )
A.如果 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,m、n是异面直线,那么 SKIPIF 1 < 0
B.如果 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,m、n是异面直线,那么n与 SKIPIF 1 < 0 相交
C.如果 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,m、n共面,那么 SKIPIF 1 < 0
D.如果 SKIPIF 1 < 0 , SKIPIF 1 < 0 ,m、n共面,那么 SKIPIF 1 < 0
5.一条直线和两条异面直线中的一条平行,则它和另一条的位置关系是( )
A.平行B.相交C.异面D.相交或异面
6.正方体的对角线与各个面上与其不共端点的对角线的位置关系是( )
A.异面垂直B.异面不垂直C.可能相交可能异面D.可能相交、平行或异面
二、填空题
7.已知四面体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的中点,且异面直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0 ,则 SKIPIF 1 < 0 _________.
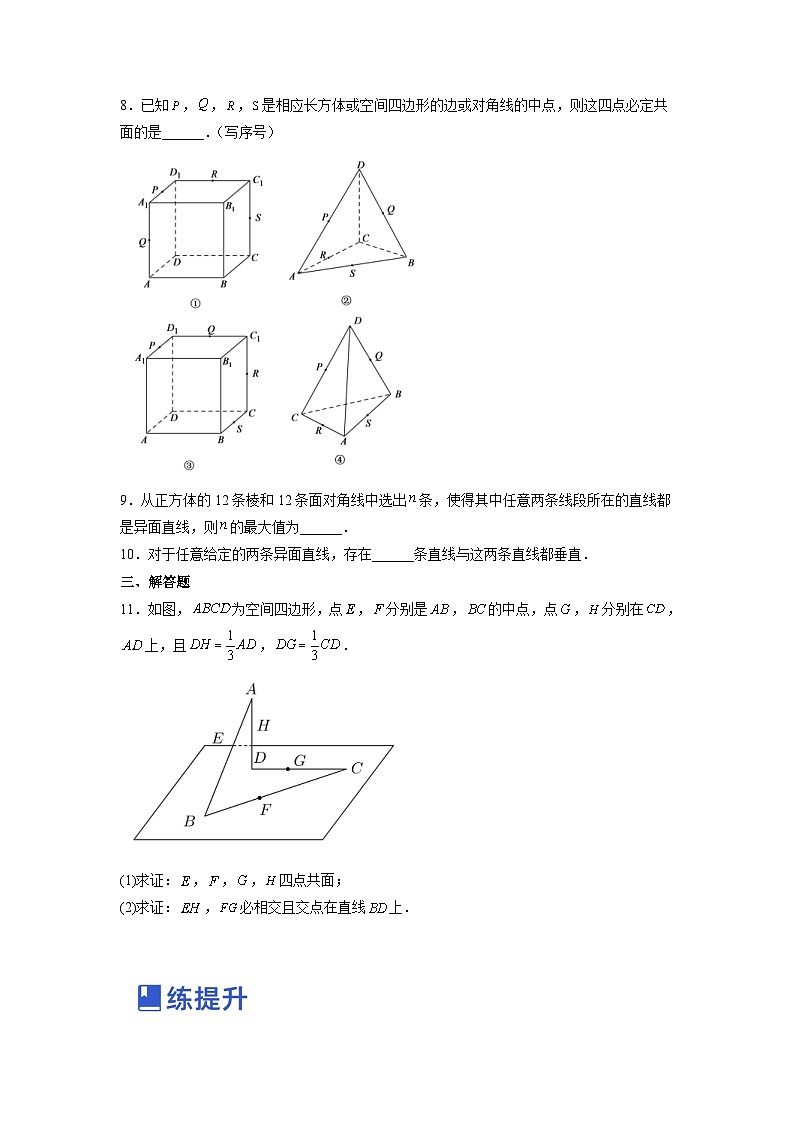
8.已知 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 是相应长方体或空间四边形的边或对角线的中点,则这四点必定共面的是______.(写序号)
9.从正方体的12条棱和12条面对角线中选出 SKIPIF 1 < 0 条,使得其中任意两条线段所在的直线都是异面直线,则 SKIPIF 1 < 0 的最大值为______.
10.对于任意给定的两条异面直线,存在______条直线与这两条直线都垂直.
三、解答题
11.如图, SKIPIF 1 < 0 为空间四边形,点 SKIPIF 1 < 0 , SKIPIF 1 < 0 分别是 SKIPIF 1 < 0 , SKIPIF 1 < 0 的中点,点 SKIPIF 1 < 0 , SKIPIF 1 < 0 分别在 SKIPIF 1 < 0 , SKIPIF 1 < 0 上,且 SKIPIF 1 < 0 , SKIPIF 1 < 0 .
(1)求证: SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 四点共面;
(2)求证: SKIPIF 1 < 0 , SKIPIF 1 < 0 必相交且交点在直线 SKIPIF 1 < 0 上.
一、单选题
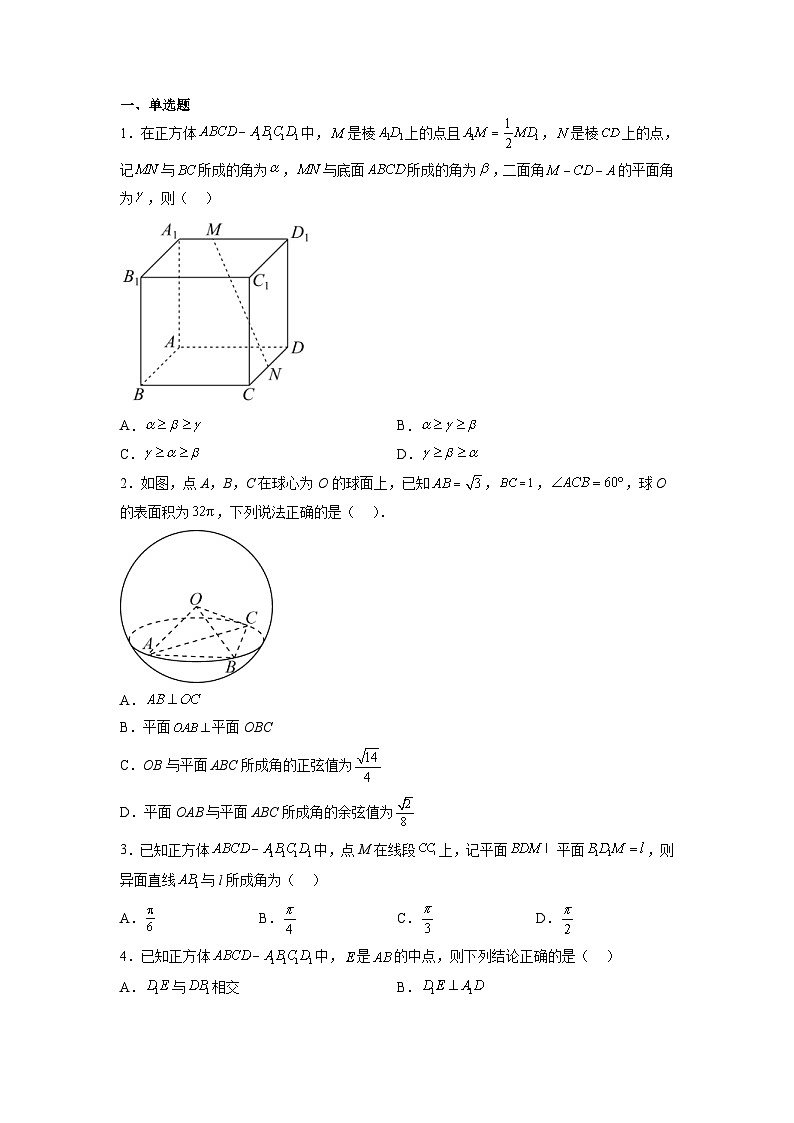
1.在正方体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 是棱 SKIPIF 1 < 0 上的点且 SKIPIF 1 < 0 , SKIPIF 1 < 0 是棱 SKIPIF 1 < 0 上的点,记 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0 , SKIPIF 1 < 0 与底面 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0 ,二面角 SKIPIF 1 < 0 的平面角为 SKIPIF 1 < 0 ,则( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.如图,点A,B,C在球心为O的球面上,已知 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 ,球O的表面积为 SKIPIF 1 < 0 ,下列说法正确的是( ).
A. SKIPIF 1 < 0
B.平面 SKIPIF 1 < 0 平面OBC
C.OB与平面ABC所成角的正弦值为 SKIPIF 1 < 0
D.平面OAB与平面ABC所成角的余弦值为 SKIPIF 1 < 0
3.已知正方体 SKIPIF 1 < 0 中,点M在线段 SKIPIF 1 < 0 上,记平面 SKIPIF 1 < 0 平面 SKIPIF 1 < 0 ,则异面直线 SKIPIF 1 < 0 与l所成角为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
4.已知正方体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 是 SKIPIF 1 < 0 的中点,则下列结论正确的是( )
A. SKIPIF 1 < 0 与 SKIPIF 1 < 0 相交B. SKIPIF 1 < 0
C. SKIPIF 1 < 0 平面 SKIPIF 1 < 0 D. SKIPIF 1 < 0 平面 SKIPIF 1 < 0
5.如图所示,在四棱柱 SKIPIF 1 < 0 中, SKIPIF 1 < 0 平面ABCD,四边形ABCD为梯形, SKIPIF 1 < 0 ,且 SKIPIF 1 < 0 ,过 SKIPIF 1 < 0 ,C,D三点的平面记为 SKIPIF 1 < 0 , SKIPIF 1 < 0 与 SKIPIF 1 < 0 的交点为Q,则以下四个结论:
① SKIPIF 1 < 0 ;
② SKIPIF 1 < 0 ;
③四棱柱被平面 SKIPIF 1 < 0 分成的上下两部分的体积相等,
④几何体 SKIPIF 1 < 0 是三棱台.
其中正确的个数为( )
A.1B.2C.3D.4
6.如图,在棱长为 SKIPIF 1 < 0 的正方体 SKIPIF 1 < 0 中,M、N、P分别是 SKIPIF 1 < 0 , SKIPIF 1 < 0 , SKIPIF 1 < 0 的中点,Q是线段 SKIPIF 1 < 0 上的动点,则下列选项中错误的是( )
A.存在点Q,使B、N、P、Q四点共面B.存在点Q,使 SKIPIF 1 < 0 平面MBN
C.三棱锥P-MBN的体积为 SKIPIF 1 < 0 D.经过C、M、B、N四点的球的表面积为 SKIPIF 1 < 0 .
二、填空题
7.如图,圆锥的底面直径 SKIPIF 1 < 0 ,其侧面展开图为半圆,底面圆的弦 SKIPIF 1 < 0 ,则异面直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成角的余弦值为___________.
8.过正方体 SKIPIF 1 < 0 的顶点 SKIPIF 1 < 0 在空间作直线 SKIPIF 1 < 0 ,使 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 和直线 SKIPIF 1 < 0 所成的角都等于 SKIPIF 1 < 0 ,则这样的直线 SKIPIF 1 < 0 共有______条.
9.正方体 SKIPIF 1 < 0 的棱长为 SKIPIF 1 < 0 ,则异面直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 间的距离等于______.
10.空间四边形 SKIPIF 1 < 0 的各边与两条对角线的长都为1,点 SKIPIF 1 < 0 在边 SKIPIF 1 < 0 上移动,点 SKIPIF 1 < 0 在边 SKIPIF 1 < 0 上移动,则点 SKIPIF 1 < 0 , SKIPIF 1 < 0 的最短距离为______.
三、解答题
11.如图所示,在正方体 SKIPIF 1 < 0 中,E,F分别是 SKIPIF 1 < 0 的中点.
(1)求证: SKIPIF 1 < 0 三线交于点P;
(2)在(1)的结论中,G是 SKIPIF 1 < 0 上一点,若FG交平面ABCD于点H,求证:P,E,H三点共线.
一、单选题
1.(2022·浙江·高考真题)如图,已知正三棱柱 SKIPIF 1 < 0 ,E,F分别是棱 SKIPIF 1 < 0 上的点.记 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0 , SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0 ,二面角 SKIPIF 1 < 0 的平面角为 SKIPIF 1 < 0 ,则( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
2.(2020·山东·高考真题)已知正方体 SKIPIF 1 < 0 (如图所示),则下列结论正确的是( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
3.(2021·全国·高考真题(理))在正方体 SKIPIF 1 < 0 中,P为 SKIPIF 1 < 0 的中点,则直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成的角为( )
A. SKIPIF 1 < 0 B. SKIPIF 1 < 0 C. SKIPIF 1 < 0 D. SKIPIF 1 < 0
二、多选题
4.(2022·全国·高考真题)已知正方体 SKIPIF 1 < 0 ,则( )
A.直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0 B.直线 SKIPIF 1 < 0 与 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0
C.直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成的角为 SKIPIF 1 < 0 D.直线 SKIPIF 1 < 0 与平面ABCD所成的角为 SKIPIF 1 < 0
5.(2021·全国·高考真题)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足 SKIPIF 1 < 0 的是( )
A.B.
C.D.
三、填空题
6.(2020·全国·高考真题(理))设有下列四个命题:
p1:两两相交且不过同一点的三条直线必在同一平面内.
p2:过空间中任意三点有且仅有一个平面.
p3:若空间两条直线不相交,则这两条直线平行.
p4:若直线l SKIPIF 1 < 0 平面α,直线m⊥平面α,则m⊥l.
则下述命题中所有真命题的序号是__________.
① SKIPIF 1 < 0 ② SKIPIF 1 < 0 ③ SKIPIF 1 < 0 ④ SKIPIF 1 < 0
四、解答题
7(理).(2021·北京·高考真题)如图:在正方体 SKIPIF 1 < 0 中, SKIPIF 1 < 0 为 SKIPIF 1 < 0 中点, SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 .
(1)求证: SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点;
(2)点 SKIPIF 1 < 0 是棱 SKIPIF 1 < 0 上一点,且二面角 SKIPIF 1 < 0 的余弦值为 SKIPIF 1 < 0 ,求 SKIPIF 1 < 0 的值.
8(理).(2021·浙江·高考真题)如图,在四棱锥 SKIPIF 1 < 0 中,底面 SKIPIF 1 < 0 是平行四边形, SKIPIF 1 < 0 ,M,N分别为 SKIPIF 1 < 0 的中点, SKIPIF 1 < 0 .
(1)证明: SKIPIF 1 < 0 ;
(2)求直线 SKIPIF 1 < 0 与平面 SKIPIF 1 < 0 所成角的正弦值.
新高考数学一轮复习讲与练第20讲 直线、平面平行垂直的判定与性质(练)(2份打包,原卷版+解析版): 这是一份新高考数学一轮复习讲与练第20讲 直线、平面平行垂直的判定与性质(练)(2份打包,原卷版+解析版),文件包含新高考数学一轮复习讲与练第20讲直线平面平行垂直的判定与性质练原卷版doc、新高考数学一轮复习讲与练第20讲直线平面平行垂直的判定与性质练解析版doc等2份试卷配套教学资源,其中试卷共38页, 欢迎下载使用。
新高考数学一轮复习讲与练第19讲 空间点、直线、平面之间的位置关系(讲)(2份打包,原卷版+解析版): 这是一份新高考数学一轮复习讲与练第19讲 空间点、直线、平面之间的位置关系(讲)(2份打包,原卷版+解析版),文件包含新高考数学一轮复习讲与练第19讲空间点直线平面之间的位置关系讲原卷版doc、新高考数学一轮复习讲与练第19讲空间点直线平面之间的位置关系讲解析版doc等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。
新高考数学一轮复习 讲与练第25讲 直线的方程(2份打包,原卷版+解析版): 这是一份新高考数学一轮复习 讲与练第25讲 直线的方程(2份打包,原卷版+解析版),文件包含新高考数学一轮复习讲与练第25讲直线的方程原卷版doc、新高考数学一轮复习讲与练第25讲直线的方程解析版doc等2份试卷配套教学资源,其中试卷共16页, 欢迎下载使用。












