







高教版(2021)拓展模块二 下册第6章 三角计算6.1 和角公式6.1.3 两角和与差的正切公式优质课ppt课件
展开6.1.3 两角和与差的正切公式
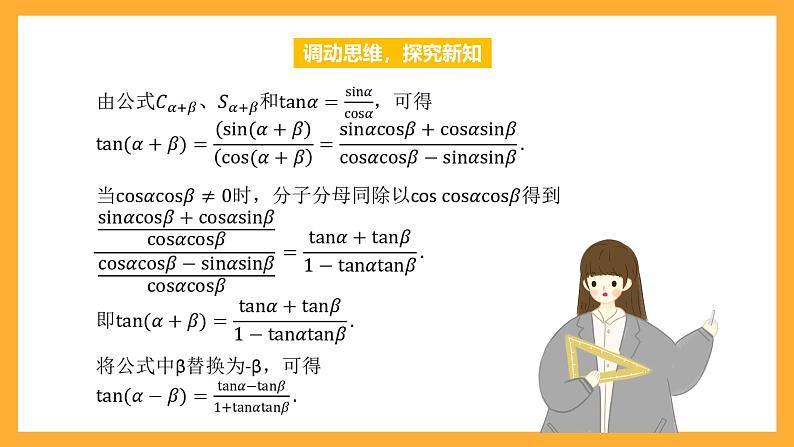
我们知道,α±β的正弦、余弦都可以用α、β的正弦与余弦表示,那么α±β的正切,即 tan(α±β),能否用α、β的正切来表示呢?
(1) 读书部分: 教材章节6.1.3; (2) 书面作业: P10习题6.1的2(3),B、3.
高教版(2021)拓展模块二 下册6.1.2 两角和与差的正弦公式完美版ppt课件: 这是一份高教版(2021)拓展模块二 下册<a href="/sx/tb_c4035820_t3/?tag_id=26" target="_blank">6.1.2 两角和与差的正弦公式完美版ppt课件</a>,文件包含中职数学高教版2021·拓展模块一下册612两角和与差的正弦公式课件pptx、中职数学高教版2021·拓展模块一下册612两角和与差的正弦公式教案doc等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。
数学拓展模块二 下册6.1.1 两角和与差的余弦公式优秀课件ppt: 这是一份数学拓展模块二 下册<a href="/sx/tb_c4035819_t3/?tag_id=26" target="_blank">6.1.1 两角和与差的余弦公式优秀课件ppt</a>,文件包含中职数学高教版2021·拓展模块一下册611两角和与差的余弦公式课件pptx、中职数学高教版2021·拓展模块一下册611两角和与差的余弦公式教案doc、余弦和角公式的推导mp4等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
数学拓展模块一(下册)6.1 和角公式教课课件ppt: 这是一份数学拓展模块一(下册)<a href="/sx/tb_c4053676_t3/?tag_id=26" target="_blank">6.1 和角公式教课课件ppt</a>,共11页。PPT课件主要包含了探索新知,典型例题,巩固练习,归纳总结,布置作业,两角和与差的正切公式,情境导入等内容,欢迎下载使用。













