



黑龙江省哈尔滨市第四中学校2023-2024学年高二下学期期末考试数学试卷(原卷版+解析版)
展开试卷满分:150分 考试时间:8:00—10:00
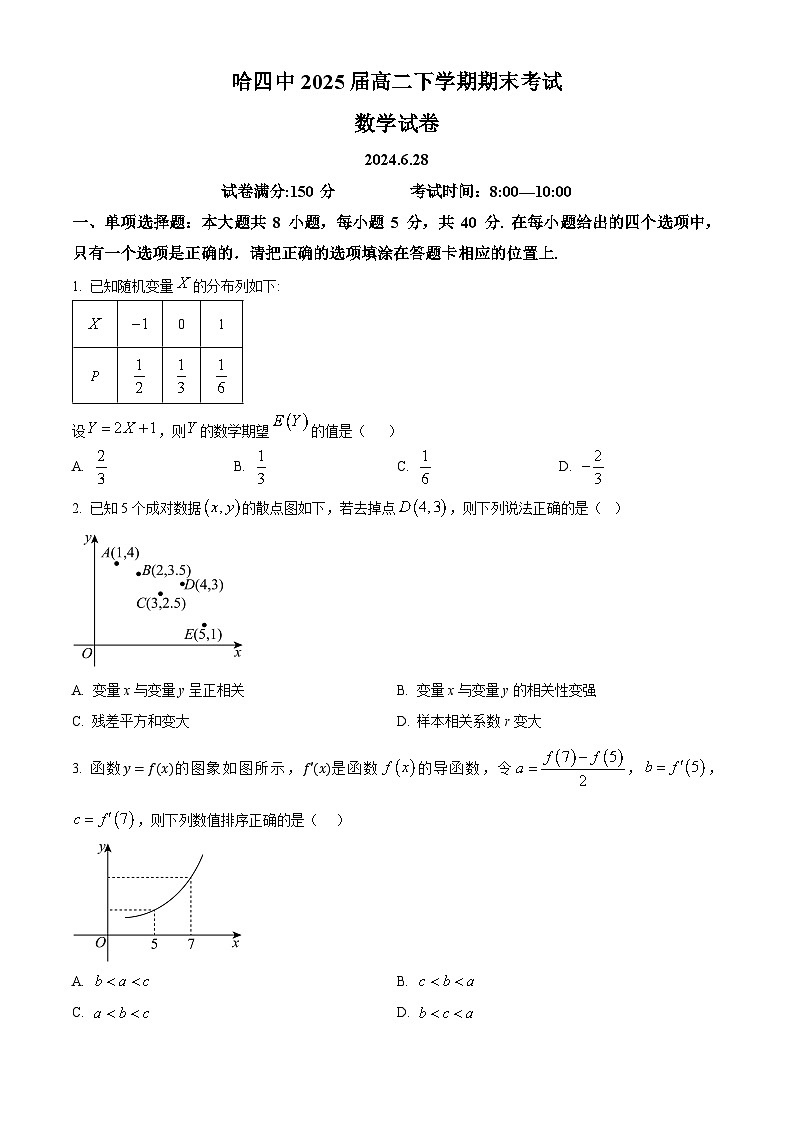
一、单项选择题:本大题共 8 小题,每小题 5 分,共 40 分. 在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1. 已知随机变量的分布列如下:
设,则的数学期望的值是( )
A. B. C. D.
2. 已知5个成对数据的散点图如下,若去掉点,则下列说法正确的是( )
A. 变量x与变量y呈正相关B. 变量x与变量y的相关性变强
C. 残差平方和变大D. 样本相关系数r变大
3. 函数y=fx的图象如图所示,f'x是函数的导函数,令,,,则下列数值排序正确的是( )
A. B.
C. D.
4. 2024年中国足球甲级联赛哈尔滨会展体育中心的主场火爆,一票难求,主办方设定了三种不同的票价分别对应球场三个不同区域的座位,四位球迷相约看球赛,则四人中恰有三人在同一区域的不同座位方式共有( )
A 30种B. 60种C. 120种D. 24种
5. 已知随机变量.若,设事件“”,事件“”,则( )
A. B. C. D.
6. 某学校在一次调查“篮球迷”的活动中,获得了如下数据,以下结论正确的是( )
附:,
A. 有的把握认为是否是篮球迷与性别有关
B. 有的把握认为是否是篮球迷与性别有关
C. 在犯错误的概率不超过的前提下,可以认为是否是篮球迷与性别有关
D. 在犯错误的概率不超过的前提下,可以认为是否是篮球迷与性别有关
7. 如图,由观测数据 的散点图可知, 与的关系可以用模型 拟合,设 ,利用最小二乘法求得 关于的回归方程 . 已知 ,,则 ( )
A B. C. 1D.
8. 当时,将三项式展开,可得到如图所示的三项展开式和“广义杨辉三角形”:
若在的展开式中,的系数为,则实数a的值为( )
A. 1B. C. 2D.
二、多项选择题:本大题共 3 小题,每小题 6 分,共 18 分. 在每小题给出的四个选项中,有多项符合题目要求. 全部选对得 6 分,选对但不全的得部分分,有选错的得0分.
9. 已知随机变量满足,且,且,则( )
A. B.
C D.
10. 下列说法正确的是( )
A. 回归分析中,线性相关系数的取值范围为
B. 回归分析中,残差图中残差比较均匀分布在以取值为0的横轴为对称轴的水平带状区域内,且宽度越窄表示拟合效果越好
C. 回归分析中,决定系数越大,说明残差平方和越小,拟合效果越好
D. 在列联表中,若每个数据均变成原来的2倍,则也变成原来的2倍(,其中)
11. 某公司为入职员工实行每月加薪,小王入职第1个月工资为a元,从第2个月到第13个月,每月比上个月增加100元,从第14个月到第25个月,每月比上个月增加50元,已知小王前3个月的工资之和为9300元,则( )
A.
B. 小王第3个月与第13个月工资之和等于第2个月与第14个月工资之和
C. 小王入职后第20个月的工资为4550元
D. 小王入职后前15个月的工资之和是55350元
三、填空题:本大题共 3 小题,每小题 5 分,共 15 分.
12. 已知函数在处的切线方程为,则________.
13. 设是等比数列an的前项和,若,,则= ______.
14. 对于等差数列和等比数列,我国古代很早就有研究成果,北宋大科学家沈括在《梦溪笔谈》中首创的“隙积术”,就是关于高阶等差级数求和的问题.现有一货物堆,从上向下查,第一层有2个货物,第二层比第一层多3个,第三层比第二层多4个,以此类推,记第层货物的个数为,则数列的前12项和________.
四、解答题:本题共 5 小题,共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15. 已知函数.
(1)求曲线过点处的切线;
(2)若曲线在点处的切线与曲线在处的切线平行,求的值.
16. 某大学组织宣传小分队进行法律法规宣传,某宣传小分队记录了前9天每天普及的人数,得到下表:
(1)从这9天的数据中任选2天的数据,以X表示2天中普及人数不少于200人的天数,求X的分布列和数学期望;
(2)由于统计人员疏忽,第5天的数据统计有误,如果去掉第5天的数据,试用剩下的数据求出每天普及的人数y关于天数x的线性回归方程.
参考数据:,,.附:对于一组数据(,),(,),……,(,),其回归直线的斜率和截距的最小二乘估计分别为:,.
17. 已知数列an满足:,且 .
(1)证明:数列bn是等比数列,并求数列an的通项公式;
(2)若,求的值.
18. 如图,四棱锥中,底面,,.
(1)若,证明:平面;
(2)若,且二面角的余弦值为,求.
19. 甲、乙两名同学玩掷骰子积分游戏,规则如下:每人的初始积分均为0分,掷1枚骰子1次为一轮,在每轮游戏中,从甲、乙两人中随机选一人掷骰子,且两人被选中的概率均为当骰子朝上的点数小于3时,掷骰子的人积2分,否则此人积1分,未掷骰子的人本轮积0分,然后进行下一轮游戏.已知每轮掷骰子的结果相互独立.
(1)求经过4轮游戏,甲的累计积分为4分的概率;
(2)经商议,甲、乙决定修改游戏规则,具体如下:甲、乙轮流掷骰子,谁掷谁积分,当骰子朝上的点数不小于3时,积2分,否则积1分,规定第一次由甲掷.记两人累计积分之和为的概率为
(i)证明:为等比数列;
(ⅱ)求 通项公式.
0
1
男生
女生
篮球迷
30
15
非篮球迷
45
10
0.10
0.05
0.01
2.706
3.841
6.635
时间x(天)
1
2
3
4
5
6
7
8
9
每天普及的人数y
80
98
129
150
203
190
258
292
310
重庆市第八中学校2023-2024学年高二下学期期末考试数学试卷(原卷及解析版): 这是一份重庆市第八中学校2023-2024学年高二下学期期末考试数学试卷(原卷及解析版),文件包含重庆市第八中学校2023-2024学年高二下学期期末考试数学试卷原卷版docx、重庆市第八中学校2023-2024学年高二下学期期末考试数学试卷解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
黑龙江省哈尔滨市第九中学校2024届高三第四次模拟考试数学试卷.(原卷版+解析版): 这是一份黑龙江省哈尔滨市第九中学校2024届高三第四次模拟考试数学试卷.(原卷版+解析版),文件包含黑龙江省哈尔滨市第九中学校2024届高三第四次模拟考试数学试卷原卷版docx、黑龙江省哈尔滨市第九中学校2024届高三第四次模拟考试数学试卷解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。
黑龙江省哈尔滨市第九中学校2023-2024学年高二下学期4月月考数学试题(原卷版+解析版): 这是一份黑龙江省哈尔滨市第九中学校2023-2024学年高二下学期4月月考数学试题(原卷版+解析版),文件包含黑龙江省哈尔滨市第九中学校2023-2024学年高二下学期4月月考数学试题原卷版docx、黑龙江省哈尔滨市第九中学校2023-2024学年高二下学期4月月考数学试题解析版docx等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












