2025年高考数学一轮复习-第4课时-直线与圆、圆与圆的位置关系【导学案】

这是一份2025年高考数学一轮复习-第4课时-直线与圆、圆与圆的位置关系【导学案】，共15页。学案主要包含了课标解读，课程标准，核心素养，命题说明，必备知识·逐点夯实，核心考点·分类突破，加练备选等内容，欢迎下载使用。

【课程标准】
1.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系.
2.能用直线和圆的方程解决一些简单的数学问题与实际问题.
【核心素养】
数学抽象、数学运算、逻辑推理.
【命题说明】
【必备知识·逐点夯实】
知识梳理·归纳
1.直线与圆的位置关系(圆心到直线的距离为d,圆的半径为r)
微点拨 判断直线与圆的位置关系,常用几何法而不用代数法.
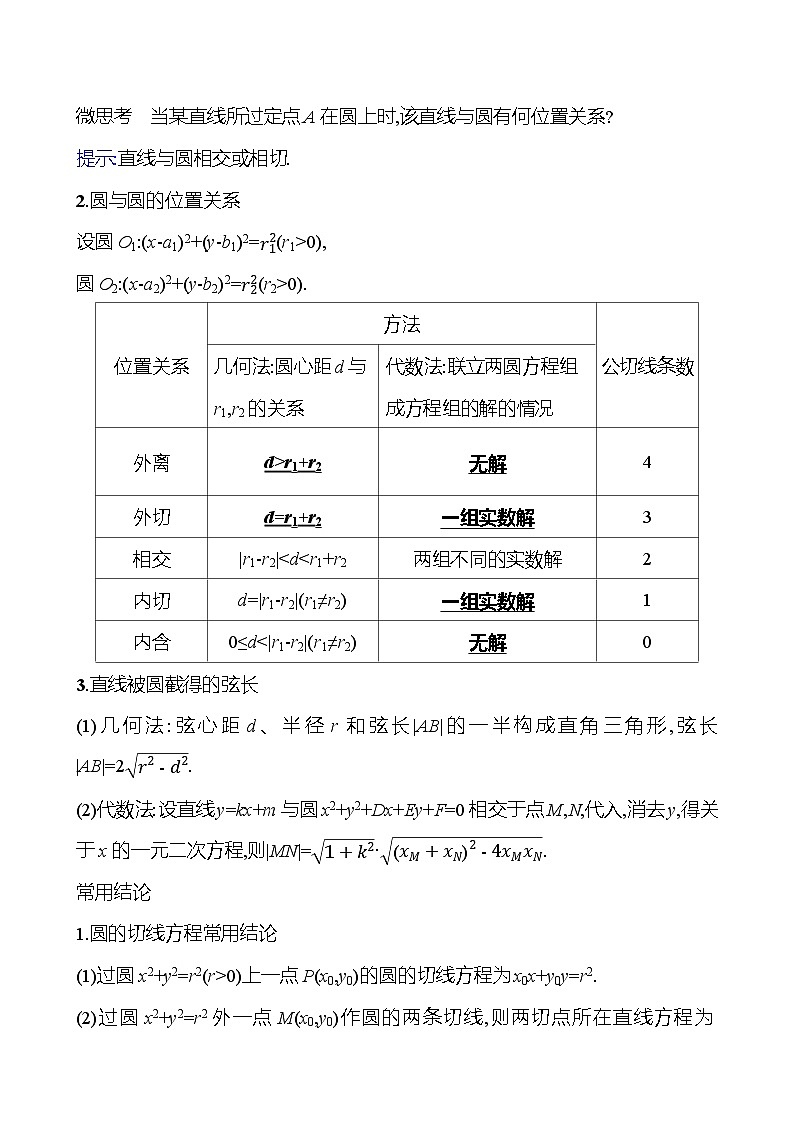
微思考 当某直线所过定点A在圆上时,该直线与圆有何位置关系?
提示:直线与圆相交或相切.
2.圆与圆的位置关系
设圆O1:(x-a1)2+(y-b1)2=r12(r1>0),
圆O2:(x-a2)2+(y-b2)2=r22(r2>0).
3.直线被圆截得的弦长
(1)几何法:弦心距d、半径r和弦长|AB|的一半构成直角三角形,弦长|AB|=2r2-d2.
(2)代数法:设直线y=kx+m与圆x2+y2+Dx+Ey+F=0相交于点M,N,代入,消去y,得关于x的一元二次方程,则|MN|=1+k2·(xM+xN)2-4xMxN.
常用结论
1.圆的切线方程常用结论
(1)过圆x2+y2=r2(r>0)上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.
(2)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为x0x+y0y=r2.
2.当两圆外切时,两圆有一条内公切线,该公切线垂直于两圆圆心的连线;当两圆内切时,两圆有一条外公切线,该公切线垂直于两圆圆心的连线.
3.两圆相交时公共弦的性质
圆C1:x2+y2+D1x+E1y+F1=0(D12+E12-4F1>0)与圆C2:x2+y2+D2x+E2y+F2 =0(D22+E22-4F2>0)相交时:
(1)将两圆方程直接作差,消去x2,y2得到两圆公共弦所在直线方程;
(2)两圆圆心的连线垂直平分公共弦;
(3)x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ∈R,λ≠-1)表示过两圆交点的圆系方程(不包括C2).
基础诊断·自测
1.(思考辨析)(正确的打“√”,错误的打“×”)
(1)若直线与圆有公共点,则直线与圆相交或相切.( √ )
提示:(1)直线与圆有一个公共点,则直线与圆相切,有两个公共点,则直线与圆相交,故(1)正确;
(2)若两圆没有公共点,则两圆一定外离.( × )
提示:(2)两圆没有公共点,则两圆外离或内含,故(2)错误;
(3)若两圆外切,则两圆有且只有一个公共点,反之也成立.( × )
提示:(3)若两圆外切,则两圆有且只有一个公共点;若两圆有且只有一个公共点,则两圆外切或内切,故(3)错误;
(4)若两圆有公共点,则|r1-r2|≤d≤r1+r2.( √ )
提示:(4)若两圆有公共点,则两圆外切或相交或内切,所以|r1-r2|≤d≤r1+r2,故(4)正确.
2.(选择性必修第一册人AP96例5变条件)圆O1:x2+y2-4y+3=0和圆O2:x2+y2-16y=0的位置关系是( )
A.外离 B.相交 C.相切 D.内含
【解析】选D.O1:x2+(y-2)2=1,O2:x2+(y-8)2=64,所以O1(0,2),r1=1,
O2(0,8),r2=8,O1O2=(0-0)2+(2-8)2=6,则O1O2=63.(选择性必修第一册人AP93练习T3变条件)直线x-y+3=0被圆(x+2)2+(y-2)2=2截得的弦长等于( )
A.62 B.3 C.23 D.6
【解析】选D.圆心(-2,2)到直线x-y+3=0的距离d=22,圆的半径r=2,解直角三角形得,半弦长为62,所以弦长等于6.
4.(2022·天津高考)若直线x-y+m=0(m>0)与圆(x-1)2+(y-1)2=3相交所得的弦长为m,则m=__________.
【解析】因为圆心C(1,1)到直线x-y+m=0(m>0)的距离d=m2,
又直线与圆相交所得的弦长为m,所以m=2r2-d2,所以m2=4(3-m22),解得m=2.
答案:2
5.(忽视直线斜率不存在的情形致误)过点P(2,2)的圆C:x2+(y-1)2=2的切线方程为______________________.
【解析】由圆C方程知:圆心C(0,1),半径r=2;
当过P的直线斜率不存在,即直线方程为
x=2时,直线与圆C相切;
设过P点且斜率存在的圆C的切线方程为y-2=k(x-2),即kx-y-2k+2=0,
则圆心C到直线的距离d=1-2kk2+1=2,即k=-24,所以该切线方程为-24x-y+52=0,
即x+22y-52=0;
综上所述:所求切线方程为x=2或x+22y-52=0.
答案:x=2或x+22y-52=0
【核心考点·分类突破】
考点一 直线与圆的位置关系
考情提示
直线与圆相切求切线方程以及直线与圆相交求弦长是高考的重点,正确利用圆心到直线的距离与半径之间的关系是解决此类问题的关键.
角度1 直线与圆的位置关系的判断
[例1](1)(一题多法)已知圆C:x2+y2-6x-8y+21=0和直线l:kx-y+3-4k=0的位置关系是( )
A.相交、相切或相离 B.相交或相切
C.相交 D.相切
【解析】选C.圆C:x2+y2-6x-8y+21=0,即(x-3)2+(y-4)2=22,圆心为C(3,4),半径为r=2.
方法一 直线l:kx-y+3-4k=0,即k(x-4)-y+3=0,所以直线l过定点B(4,3).
(4-3)2+(3-4)2=2<4,所以点B(4,3)在圆C内,所以直线l与圆C相交.
方法二 圆心C(3,4)到直线l:kx-y+3-4k=0的距离为
|3k-4+3-4k|1+k2=|k+1|1+k2=k2+2k+11+k2=1+2k1+k2≤2<4,所以直线与圆相交.
(2)(多选题)(2021·新高考Ⅱ卷)已知直线l:ax+by-r2=0与圆C:x2+y2=r2,点A(a,b),则下列说法正确的是( )
A.若点A在圆C上,则直线l与圆C相切
B.若点A在圆C内,则直线l与圆C相离
C.若点A在圆C外,则直线l与圆C相离
D.若点A在直线l上,则直线l与圆C相切
【解析】选ABD.圆心C(0,0)到直线l的距离d=r2a2+b2,若点A(a,b)在圆C上,
则a2+b2=r2,所以d=r2a2+b2=r,则直线l与圆C相切,故A正确;
若点A(a,b)在圆C内,则a2+b2r,
则直线l与圆C相离,故B正确;
若点A(a,b)在圆C外,则a2+b2>r2,所以d=r2a2+b2则直线l与圆C相交,故C错误;
若点A(a,b)在直线l上,则a2+b2-r2=0,即a2+b2=r2,所以d=r2a2+b2=r,
则直线l与圆C相切,故D正确.
解题技法
判断直线与圆的位置关系的一般方法
(1)几何法:圆心到直线的距离与圆半径比较大小,特点是计算量较小;
(2)代数法:将直线方程与圆方程联立方程组,通过解的情况判断,适合于判断直线与圆的位置关系.
角度2 弦长问题
[例2](2024·昆明模拟)已知直线y=2x与圆(x-2)2+(y-2)2=1交于A,B两点,则AB=( )
A.55 B.255 C.355 D.455
【解析】选B.因为圆的方程为(x-2)2+(y-2)2=1,
所以圆心坐标为(2,2),半径r=1,
则圆心(2,2)到直线y=2x的距离d=2×2-222+1=255,
所以弦长AB=2r2-d2=21-45=255.
解题技法
直线和圆相交弦长的两种求法
(1)代数法:将直线和圆的方程联立方程组,根据弦长公式求弦长.
(2)几何法:若弦心距为d,圆的半径长为r,则弦长l=2r2-d2.
根据弦长求直线方程时要注意验证斜率不存在的情况.
角度3 切线问题
[例3]已知点P(2+1,2-2),点M(3,1),圆C:(x-1)2+(y-2)2=4.
(1)求过点P的圆C的切线方程;
【解析】由题意得圆心C(1,2),半径r=2.
(1)因为(2+1-1)2+(2-2-2)2=4,
所以点P在圆C上.
又kPC=2-2-22+1-1=-1,
所以切线的斜率k=-1kPC=1.
所以过点P的圆C的切线方程是y-(2-2)=x-(2+1),即x-y+1-22=0.
(2)求过点M的圆C的切线方程,并求出切线长.
【解析】(2)因为(3-1)2+(1-2)2=5>4,所以点M在圆C外部.
当过点M的直线斜率不存在时,直线方程为x=3,即x-3=0.
又点C(1,2)到直线x-3=0的距离d=3-1=2=r,
即此时满足题意,所以直线x=3是圆的切线.
当切线的斜率存在时,设切线方程为y-1=k(x-3),
即kx-y+1-3k=0,
则圆心C到切线的距离d=|k-2+1-3k|k2+1=r=2,解得k=34.
所以切线方程为y-1=34(x-3),即3x-4y-5=0.
综上可得,过点M的圆C的切线方程为x-3=0或3x-4y-5=0.
因为|MC|=(3-1)2+(1-2)2=5,
所以过点M的圆C的切线长为|MC|2-r2=5-4=1.
解题技法
1.过一点求圆的切线方程的两种求法
(1)代数法:设切线方程为y-y0=k(x-x0),与圆的方程组成方程组,消元后得到一个一元二次方程,然后令判别式Δ=0进而求得k.注意斜率不存在的情况.
(2)几何法:设切线方程为y-y0=k(x-x0),利用点到直线的距离公式表示出圆心到切线的距离d,然后令d=r,进而求出k.注意斜率不存在的情况.
特别地,当点在圆上时,可直接利用圆心与切点的连线的斜率及切线的性质求切线方程.
2.过圆外一点P引圆的切线,求切线长时,常利用点P、圆心、切点构成的直角三角形求解.
对点训练
1.(2024·南京模拟)直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是( )
A.过圆心 B.相切
C.相离 D.相交但不过圆心
【解析】选D.由题意知,圆(x-1)2+(y+1)2=9的圆心为(1,-1),半径r=3,
则圆心到直线3x+4y+12=0的距离d=3×1+4×(-1)+1232+42=115,
因为02.过点(-33,0)且倾斜角为π3的直线l交圆x2+y2-6y=0于A,B两点,则弦AB的长
为( )
A.42 B.22 C.210 D.10
【解析】选A.过点(-33,0)且倾斜角为π3的直线l的方程为y=3(x+33),即3x-y+1=0,
又圆x2+y2-6y=0即x2+(y-3)2=9,所以圆心(0,3),半径r=3,
则圆心(0,3)到直线l的距离d=|-3+1|2=1,
所以直线被圆截得的弦AB=232-12=42.
3.(2024·东城模拟)已知点M(1,3)在圆C:x2+y2=m上,过M作圆C的切线l,则l的倾斜角为( )
A.30° B.60° C.120° D.150°
【解析】选D.由题意得m=1+3=4,
当l的斜率不存在时,此时直线方程为x=1,与圆C:x2+y2=4相交,不符合题意;
当l的斜率存在时,设切线l的方程为y-3=k(x-1),
则|k-3|1+k2=2,解得k=-33,因为l的倾斜角为0°≤θ<180°,故l的倾斜角为150°.
【加练备选】
(2024·宜春模拟)已知圆C经过三点O(0,0),A(1,1),B(4,2).
(1)求圆C的方程;
【解析】(1)设圆C的方程为x2+y2+Dx+Ey+F=0(D2+E2-4F>0),
由圆C经过三点O(0,0),A(1,1),B(4,2),
得F=02+D+E+F=020+4D+2E+F=0,解得D=-8E=6F=0,
所以圆C的方程为x2+y2-8x+6y=0.
(2)经过点M(1,-4)的直线l被圆C所截得的弦长为45,求直线l的方程.
【解析】(2)由(1)知圆C:(x-4)2+(y+3)2=25,即圆心C(4,-3),半径为5,
由直线l被圆C所截得的弦长为45,得圆心C到直线l的距离d=52-(25)2=5,
而直线l经过点M(1,-4),显然直线l的斜率存在,设直线l的方程为y+4=k(x-1),
即kx-y-4-k=0,于是d=4k+3-4-kk2+1=5,得k=2或k=-12,
所以直线l的方程为2x-y-6=0或x+2y+7=0.
考点二 圆与圆的位置关系
[例4](1)已知圆E的圆心在y轴上,且与圆x2+y2-2x=0的公共弦所在直线的方程为x-3y=0,则圆E的方程为( )
A.x2+(y-3)2=2B.x2+(y+3)2=2
C.x2+(y-3)2=3D.x2+(y+3)2=3
【解析】选C.两圆圆心连线与公共弦垂直,不妨设所求圆心的坐标为(0,a),
半径为r.
又圆x2+y2-2x=0的圆心为(1,0),半径为1,故a-1×13=-1,解得a=3.
故所求圆心为(0,3).点(1,0)到直线x-3y=0的距离为11+3=12,
所以x2+y2-2x=0截直线x-3y=0所得弦长为212-14=3,圆心(0,3)到直线x-3y=0的距离为32,
所以圆截直线x-3y=0所得弦长为2r2-(32) 2=3,解得r=3.
故圆心坐标为(0,3),半径为3.
得圆E的方程为x2+(y-3)2=3.
(2)已知两圆C1:x2+y2-2x+10y-24=0和C2:x2+y2+2x+2y-8=0.
①判断两圆公切线的条数;
【解析】①两圆的标准方程分别为C1:(x-1)2+(y+5)2=50,
C2:(x+1)2+(y+1)2=10,
则圆C1的圆心为(1,-5),半径r1=52;
圆C2的圆心为(-1,-1),半径r2=10.
又|C1C2|=25,r1+r2=52+10,r1-r2=52-10,
所以r1-r2<|C1C2|所以两圆有两条公切线.
②求公共弦所在的直线方程以及公共弦的长度.
【解析】②将两圆方程相减,得公共弦所在直线方程为x-2y+4=0.圆心C1到直线x-2y+4=0的距离d=|1-2×(-5)+4|1+(-2)2=35,
设公共弦长为2l,由勾股定理得r2=d2+l2,
得50=45+l2,解得l=5,所以公共弦长2l=25.
一题多变
[变式1]本例(2)中,若两圆相交于A,B两点,不求交点,则线段C1C2(C1,C2分别为两个圆的圆心)的垂直平分线所在的直线方程为______________.
【解析】由圆C1的圆心坐标为(1,-5),圆C2的圆心坐标为(-1,-1),可知kC1C2=-5-(-1)1-(-1)=-2,则kAB=12,C1C2的中点坐标为(0,-3),
因此线段C1C2的垂直平分线所在的直线方程为y+3=12x,即x-2y-6=0.
答案:x-2y-6=0
[变式2]本例(2)中的两圆若相交于两点A,B,则经过两点A,B且圆心在直线x+y=0上的圆的方程为______________.
【解析】设所求的圆的方程为x2+y2-2x+10y-24+λ(x2+y2+2x+2y-8)=0(λ≠-1),
整理可得(1+λ)x2+(1+λ)y2+(2λ-2)x+(2λ+10)y-8λ-24=0,
因此圆的圆心坐标为(1-λ1+λ,-λ+51+λ),由于圆心在x+y=0上,则1-λ1+λ+(-λ+51+λ)=0,
解得λ=-2,
因此所求的圆的方程为x2+y2+6x-6y+8=0.
答案:x2+y2+6x-6y+8=0
解题技法
圆与圆的位置关系问题的解题策略
(1)判断两圆位置关系常用几何法,即用两圆圆心距与两圆半径和及差的绝对值的大小关系判断.
(2)两圆相交时,两圆的公共弦所在直线的方程,可由两圆的方程作差消去x2,y2项得到.
(3)求两圆公共弦长,常选其中一圆,由弦心距d、半弦长l2、半径r构成直角三角形,利用勾股定理求解.
考点三 与圆有关的最值、范围问题
[例5](2024·沈阳模拟)已知实数x,y满足方程x2+y2-4x+1=0.求:
(1)yx的取值范围;
【解析】(1)由圆的一般方程可得:圆心为(2,0),半径r=3;
因为02+02-4×0+1=1>0,
所以原点在圆x2+y2-4x+1=0的外部,
设yx=k,则kx-y=0(x≠0)与圆x2+y2-4x+1=0有公共点,
所以圆心(2,0)到kx-y=0(x≠0)的距离d=2kk2+1≤3,
解得-3≤k≤3,
即yx的取值范围为-3,3.
(2)y-x的取值范围;
【解析】(2)设y-x=m,则直线x-y+m=0与圆x2+y2-4x+1=0有公共点,所以圆心(2,0)到x-y+m=0的距离d=2+m2≤3,
解得-6-2≤m≤6-2,
即y-x的取值范围为-6-2,6-2.
(3)x2+y2的取值范围.
【解析】(3)由(1)知:原点在圆x2+y2-4x+1=0的外部,
则可设x2+y2=r2(r>0),则圆x2+y2=r2(r>0)与圆x2+y2-4x+1=0有公共点,
因为两圆圆心距d=(0-2)2+(0-0)2=2,
所以r-3≤2≤r+3,
解得2-3≤r≤2+3,
所以7-43≤r2≤7+43,
即x2+y2的取值范围为7-43,7+43.
解题技法
关于圆上点(x,y)有关代数式的最值问题的解法
对点训练
(多选题)(2024·盐城模拟)已知实数x,y满足曲线C的方程x2+y2-2x-2=0,则下列选项正确的是( )
A.x2+y2的最大值是3+1
B.y+1x+1的最大值是2+6
C.|x-y+3|的最小值是22-3
D.过点(0,2)作曲线C的切线,则切线方程为x-2y+2=0
【解析】选BD.由圆C:x2+y2-2x-2=0可化为(x-1)2+y2=3,可得圆心(1,0),半径r=3,
对于A,由x2+y2表示圆C上的点到定点(0,0)的距离的平方,所以它的最大值为[(1-0)2+02+3]2=4+23,所以A错误;
对于B,y+1x+1表示圆上的点与点(-1,-1)的斜率,设y+1x+1=k,即y+1=k(x+1),
由圆心(1,0)到直线y+1=k(x+1)的距离d=2k-1k2+1≤3,
解得2-6≤k≤2+6,
所以y+1x+1的最大值为2+6,所以B正确;
对于C,由x-y+3表示圆上任意一点到直线x-y+3=0的距离的2倍,圆心到直线的距离d=42=22,所以其最小值为2(22-3)=4-6,所以C错误;
对于D,因为点(0,2)满足圆C的方程,
即点(0,2)在圆C上,
则该点与圆心连线的斜率为k1=-2,
根据圆的性质,可得过点(0,2)作圆C的切线的斜率为k=-1k1=22,
所以切线方程为y-2=22(x-0),
即x-2y+2=0,所以D正确.
【加练备选】
已知点P(x,y)在圆:x2+(y-1)2=1上运动.试求:
(1)(x+3)2+y2的最值;
【解析】(1)设圆x2+(y-1)2=1的圆心为A(0,1),半径r=1,点P(x,y)在圆上,
所以(x+3)2+y2表示P(x,y)到定点E(-3,0)的距离的平方,
因为|AE|=(3)2+12=2,
所以|AE|-r≤|PE|≤|AE|+r,
即1≤|PE|≤3,所以1≤(x+3)2+y2≤9,
即(x+3)2+y2的最大值为9,最小值为1;
(2)y-1x-2的最值.
【解析】(2)点P(x,y)在圆上,则y-1x-2表示圆上的点P与点B(2,1)连线的斜率,
根据题意画出图形,当P与C(或D)重合时,直线BC(BD)与圆A相切,
设直线BC的解析式为y-1=k(x-2),即kx-y-2k+1=0,
所以圆心(0,1)到直线BC的距离d=r,即|-2k|k2+1=1,解得k=±33,
所以-33≤y-1x-2≤33,所以y-1x-2的最大值为33,最小值为-33.
考向
考法
直线与圆、圆与圆的位置关系是高考的热点内容之一,其中直线与圆相切及直线与圆相交是重点考查的内容,多以选择题或填空题的形式出现.
预测
预计2025年高考直线与圆、圆的位置关系仍会出题,一般在选择题或填空题中出现.
位置关系
相离
相切
相交
图形
量化
方程观点
Δ<0
Δ=0
Δ>0
几何观点
d>r
d=r
d位置关系
方法
公切线条数
几何法:圆心距d与r1,r2的关系
代数法:联立两圆方程组成方程组的解的情况
外离
d>r1+r2
无解
4
外切
d=r1+r2
一组实数解
3
相交
|r1-r2|两组不同的实数解
2
内切
d=|r1-r2|(r1≠r2)
一组实数解
1
内含
0≤d<|r1-r2|(r1≠r2)
无解
0
类型
辨析
改编
易错
高考
题号
1
2,3
5
4
代数式特征
求解方法
u=y-bx-a
转化为过点(a,b)和点(x,y)的直线的斜率的最值
t=ax+by
转化为动直线的截距的最值
(x-a)2+(y-b)2
转化为动点(x,y)到定点(a,b)的距离平方的最值