2025高考数学一轮复习-3.2-导数与函数的单调性-专项训练【含解析】

这是一份2025高考数学一轮复习-3.2-导数与函数的单调性-专项训练【含解析】，共12页。
A. −4 B. −1 C. 1 D. 4
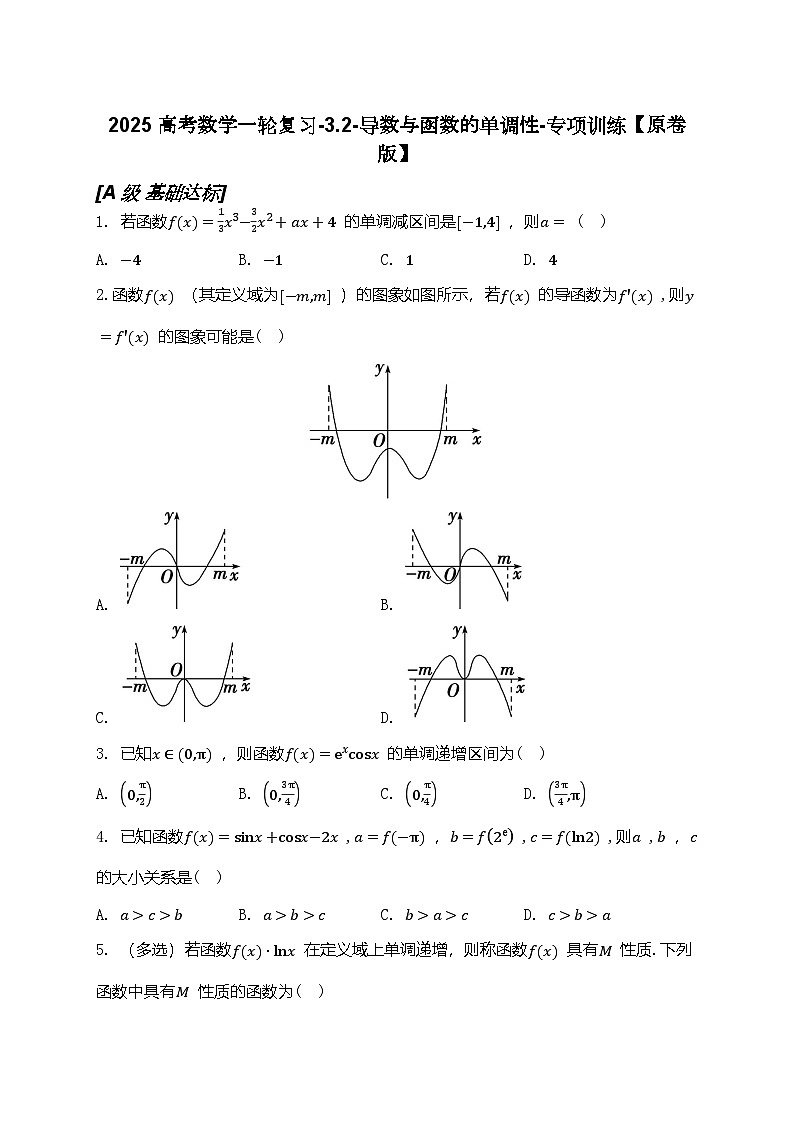
2.函数fx （其定义域为[−m,m] ）的图象如图所示，若fx 的导函数为f′x ,则y=f′x 的图象可能是( )
A. B.
C. D.
3. 已知x∈0,π ，则函数fx=excsx 的单调递增区间为( )
A. 0,π2 B. 0,3π4 C. 0,π4 D. 3π4,π
4. 已知函数fx=sinx+csx−2x ,a=f−π ，b=f2e ,c=fln2 ,则a ,b ，c 的大小关系是( )
A. a>c>b B. a>b>c C. b>a>c D. c>b>a
5. （多选）若函数fx⋅lnx 在定义域上单调递增，则称函数fx 具有M 性质.下列函数中具有M 性质的函数为( )
A. fx=1e B. fx=x−1 C. fx=1ex D. fx=ex
6. 已知函数y=fxx∈R 的图象如图所示，则不等式xf′x≥0 的解集为 .
7.设函数fx=alnx+bx2 ,若函数fx 的图象在点1,f1 处的切线方程为y=x ,则函数y=fx 的单调递增区间为 .
8.已知函数fx 的定义域为D ，给出下列三个条件：①∀x∈D ，有fx+f−x=0 ；②∀x∈D ，有f′x≤0 ；③∃x1 ,x2∈D 且x1a B. c>a>b C. c>b>a D. b>a>c
16. 已知函数fx=alnx−ax−3a∈R .
（1） 求函数fx 的单调区间；
（2） 若函数y=fx 的图象在点2,f2 处的切线的倾斜角为45∘ ，对于任意的t∈[1,2] ,函数gx=x3+x2⋅f′x+m2 在区间t,3 上总不是单调函数，求实数m 的取值范围.
2025高考数学一轮复习-3.2-导数与函数的单调性-专项训练【解析版】
[A级 基础达标]
1. 若函数fx=13x3−32x2+ax+4 的单调减区间是[−1,4] ，则a= ( A )
A. −4 B. −1 C. 1 D. 4
[解析]选A.易知f′x=x2−3x+a ,由题意知f′x≤0 的解集为[−1,4] ,则−1 与4是方程x2−3x+a=0 的两个根，故a=−1×4=−4 .
2.函数fx （其定义域为[−m,m] ）的图象如图所示，若fx 的导函数为f′x ,则y=f′x 的图象可能是( A )
A. B.
C. D.
[解析]选A.由fx 的图象知fx 在−m,0 上先减后增，故f′x 在−m,0 上先负后正，同理f′x 在0,m 上先负后正，结合选项，只有选项A符合.故选A.
3. 已知x∈0,π ，则函数fx=excsx 的单调递增区间为( C )
A. 0,π2 B. 0,3π4 C. 0,π4 D. 3π4,π
[解析]选C.由题，f′x=excsx−sinx ,令f′x>0 ,即csx−sinx>0 ，因为x∈0,π ,所以0b B. a>b>c C. b>a>c D. c>b>a
[解析]选A.函数fx 的定义域为R ，f′x=csx−sinx−2=2csx+π4−2≤2−20 恒成立，符合题意；
对于B，gx=x−1lnx ,x∈0,+∞ ,则g′x=lnx−1x+1 ,又lnx−1x+1′=1x+1x2>0 ,g′1=0 ,所以当022 ，所以函数y=fx 的单调递增区间为22,+∞ .
8.已知函数fx 的定义域为D ，给出下列三个条件：①∀x∈D ，有fx+f−x=0 ；②∀x∈D ，有f′x≤0 ；③∃x1 ,x2∈D 且x10 得x>2 ；由f′x−3 且a≠0 .故选BD.
11. （多选）已知函数fx=ex+e−x−2csx ,则下列说法正确的是( AD )
A. 函数y=fx 是偶函数，且在−∞,+∞ 上不单调
B. 函数y=f′x 是奇函数，且在−∞,+∞ 上不单调递增
C. 函数y=fx 在−π2,0 上单调递增
D. 对任意m∈R ,都有fm=fm ，且fm≥0
[解析]选AD.函数fx 的定义域为R ，且f−x=e−x+ex−2cs−x=ex+e−x−2csx=fx ,即函数fx 为偶函数,在−∞,+∞ 上显然不单调，故A正确；
又f′x=ex−e−x+2sinx ,所以f′−x=e−x−ex−2sinx=−f′x ,
所以函数y=f′x 是奇函数，因为f″x=ex+e−x+2csx≥2+2csx≥0 恒成立，
所以y=f′x 在−∞,+∞ 上单调递增，故B错误；
当x∈−π2,0 时，sinx0 ，且a≠1 ,函数fx=ax,x0 ，
当a≤0 时，f′x>0 恒成立，所以函数fx 在0,+∞ 上单调递增；
当a>0 时，令f′x>0 ，解得0c>a B. c>a>b C. c>b>a D. b>a>c
[解析]选A.依题意,a=e−lg2−lg5=e−lg10=e−1 ，c=3−12ln9=3−ln3=eln3−ln3 .
构造函数fx=ex−x ，定义域为0,+∞ ，
则f′x=ex−1>0 ，所以函数fx 在0,+∞ 上单调递增，
因为e≈2.718 ，e5≈148.3 ，又34=81 ，则e5>34 ，则4ln3