2025版高考数学全程一轮复习第四章三角函数与解三角形第六节函数y＝Asinωx＋φ的图象及应用课件

这是一份2025版高考数学全程一轮复习第四章三角函数与解三角形第六节函数y＝Asinωx＋φ的图象及应用课件，共53页。PPT课件主要包含了课前自主预习案，课堂互动探究案，ωx＋φ，答案C，答案D，答案BCD，答案ACD，答案A，答案B等内容，欢迎下载使用。

必 备 知 识1.函数y＝A sin (ωx＋φ)的有关概念
2.用“五点法”画y＝A sin (ωx＋φ)(A>0，ω>0)一个周期内的简图时，要找五个特征点
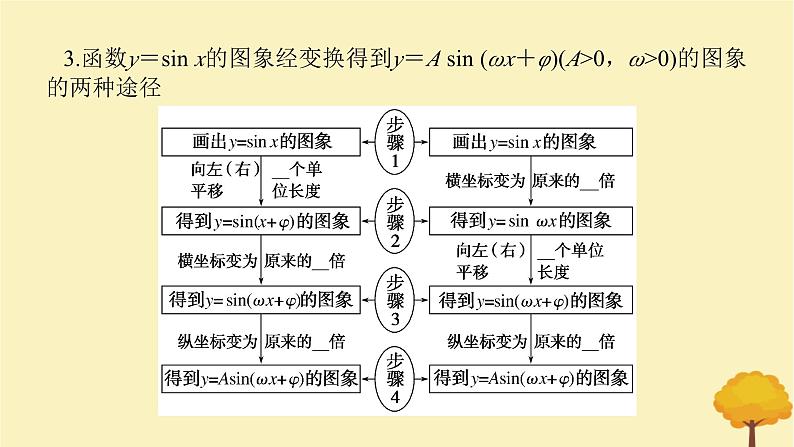
3.函数y＝sin x的图象经变换得到y＝A sin (ωx＋φ)(A>0，ω>0)的图象的两种途径
3．(教材改编)已知函数f(x)＝A sin (ωx＋φ)(A>0，ω>0，0<φ<π)在一个周期内的图象如图所示，则函数f(x)的解析式为____________．
1.了解函数y＝A sin (ωx＋φ)的实际意义．2．能画出y＝A sin (ωx＋φ)的图象，了解参数A，ω，φ对函数图象变化的影响．3．会用三角函数解决一些简单的实际问题．
问题思考·夯实技能【问题1】　如图所示为函数y＝sin (ωx＋φ)的部分图象．利用零点代入求φ时，ωx1＋φ，ωx2＋φ取哪些值？
提示：若利用x1这样的零点(图象经过(x1，0)时函数单调递减)代入求φ的值，应令ωx1＋φ＝π＋2kπ(k∈Z)；而如果利用x2这样的零点(图象经过(x2，0)时函数单调递增)代入求φ的值，应令ωx2＋φ＝2kπ(k∈Z)，应注意区分，不能笼统地令ωx＋φ＝kπ(k∈Z)．
【变式练习】　本例条件不变，第(2)问改为：函数y＝f(x)的图象可由函数y＝cs x的图象经过怎样的变换得到？
题后师说作函数y＝A sin (ωx＋φ)(A>0，ω>0)的图象常用的方法
题后师说根据三角函数图象求解析式，重在对A，ω，φ的理解，主要从以下三个方面考虑：(1)根据最大值或最小值求出A的值．(2)根据周期求出ω的值．(3)求φ的常用方法如下：①代入法：把图象上的一个已知点的坐标代入(此时要注意该点的位置)或把图象的最高点或最低点的坐标代入．②五点法：确定φ的值时，往往以寻找“五点法”中的特殊点作为突破口．
题后师说研究y＝A sin (ωx＋φ)的性质时可将ωx＋φ视为一个整体，利用换元法和数形结合思想进行解题．
题后师说利用三角函数图象解决方程的根或零点问题的方法(1)研究函数y＝A sin (ωx＋φ)在给定区间上零点个数问题时，仍然采用整体换元的方法，将ωx＋φ作为一个整体，结合函数的周期性确定ωx＋φ的范围，从而解决问题．(2)将方程的根转化为两函数图象的交点问题，结合三角函数的周期性，建立不等式组进行求解．
角度三　三角函数模型的简单应用例 5 (多选)[2024·湖南株洲模拟]如图(1)是一段依据正弦曲线设计安装的过山车轨道．建立平面直角坐标系如图(2)，h(单位：m)表示在时间t(单位：s)时，过山车(看作质点)离地平面的高度．轨道最高点P距离地平面50 m．最低点Q距离地平面10 m．入口处M距离地平面20 m．当t＝4 s时，过山车到达最高点P，t＝10 s时，过山车到达最低点Q.
题后师说三角函数模型的应用体现在两个方面：一是已知函数模型求解数学问题；二是把实际问题抽象转化成数学问题，利用三角函数的有关知识解决问题．