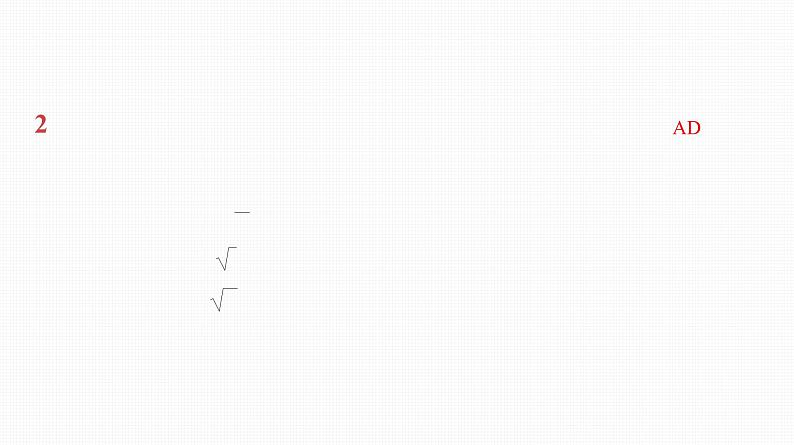
2025高考数学一轮复习-第6讲-函数的概念及其表示方法【课件】

这是一份2025高考数学一轮复习-第6讲-函数的概念及其表示方法【课件】，共53页。PPT课件主要包含了激活思维，函数的概念及表示，聚焦知识，定义域，对应关系，对函数概念的理解，举题说法，答案A，函数的定义域，函数的解析式等内容，欢迎下载使用。

1．下列图象表示函数关系y＝f(x)的是(　　)
(－∞，1)∪(1，4]
由题意得f(1)＝5，f(－3)＝21，所以f(1)＋f(－3)＝26.
5．给定函数f(x)＝－x＋1，g(x)＝(x－1)2，x∈R，m(x)＝min{f(x)，g(x)}，则m(x)＝________________________________．
2．分段函数若一个函数的定义域分成了若干个子区间，且每个子区间的解析式不同，则这种函数称为分段函数．3．定义域的求法(1) 分母不为0；偶次根式被开方数非负； 零指数幂底数不为0；实际问题有意义；对数的真数大于0，底数大于0且不等于1；(2) 复合函数的定义域：只要对应法则相同，括号里整体的取值范围就完全相同．
对于f：x→y＝x2，取x＝4时，在N＝{x|0≤x≤2}中无元素与之对应，不满足函数定义，B错误；对于f：x→y＝|x|，当x＝4时，在N＝{x|0≤x≤2}中无元素与之对应，不满足函数定义，C错误；对于f：x→y＝x－1，当x＝4时，在N＝{x|0≤x≤2}中无元素与之对应，不满足函数定义，D错误．
(2) 已知集合A＝{x|0≤x≤4}，集合B＝{x|0≤x≤2}，下列图象能建立从集合A到集合B的函数关系的是(　　)
对于A，存在点使一个x与两个y对应，不符合，排除；对于B，当2＜x≤4时，没有与之对应的y，不符合，排除；对于C，y的范围超出了集合B的范围，不符合，排除；对于D，满足函数关系的条件，正确．
对于B，若f：x→y，y＝2x，则集合A中的元素2，在集合B中没有元素与之对应，所以不能构成集合A到B的函数，不符合题意；
对于C，若f：x→y，y＝2x，则集合A中的元素2，在集合B中没有元素与之对应，所以不能构成集合A到B的函数，不符合题意；对于D，若f：x→y，y＝x，则集合A中的元素2，在集合B中没有元素与之对应，所以不能构成集合A到B的函数，不符合题意．
由题意知，ax2－4ax＋2＞0的解集为R.当a＝0时，2＞0恒成立，满足题意；
(3) 已知f(x)＋2f(－x)＝3x2－x，求f(x).
因为函数定义域为R，所以ax2＋ax＋2≠0在x∈R上恒成立．当a＝0时，ax2＋ax＋2＝2≠0满足要求；当a≠0时，要满足Δ＝a2－8a＜0，解得0＜a＜8.综上，0≤a＜8.
(2) 已知f(x)是一次函数，且满足3f(x＋1)－2f(x－1)＝2x＋17，求f(x)；
(待定系数法)设f(x)＝ax＋b(a≠0)，则3f(x＋1)－2f(x－1)＝3ax＋3a＋3b－2ax＋2a－2b＝ax＋b＋5a＝2x＋17，所以a＝2，b＝7，所以f(x)＝2x＋7.
变式　(1) 已知二次函数f(x)满足f(2x)＋f(x－1)＝10x2－7x＋5，求f(f(1))；
当a≤0时，f(a)＝a2＋1＝1，解得a＝0；当a＞0时，f(a)＝ln a＝1，解得a＝e.
令f(a)＝t，则f(t)＝2，可得t＝0或t＝1.当t＝0时，即f(a)＝0，显然a≤0，因此a＋2＝0⇒a＝－2；当t＝1时，即f(a)＝1，显然a≤0，因此a＋2＝1⇒a＝－1.综上所述，a＝－2或－1.
要使得函数有意义，则4－x2≥0，且x＋1≠0，解得x∈[－2，－1)∪(－1，2].
f(9)＝f(f(14))＝f(2×14－15)＝f(13)＝2×13－15＝11.
4．设f(x)为一次函数，且f(f(x))＝4x－1.若f(3)＝－5，则f(x)的解析式为(　　)A．f(x)＝2x－11或f(x)＝－2x＋1B．f(x)＝－2x＋1C．f(x)＝2x－11D．f(x)＝2x＋1
综上所述，f(x)＝－2x＋1.
A组　夯基精练一、 单项选择题1．下列选项中表示同一个函数的是(　　)
对于A，因为f(x)的定义域为(－∞，0)∪(0，＋∞)，而g(x)的定义域为R，所以两函数的定义域不同，故不能表示同一个函数；对于B，因为f(x)的定义域为R，而g(x)的定义域为(－∞，0)∪(0，＋∞)，所以两函数的定义域不同，故不能表示同一个函数；
f(9)＝f(9－3)＝f(6)＝f(3)＝f(0)＝20＋1＝2.
4．若函数f(x)＝lg (ax2－2x＋a)的定义域为R，则实数a的取值范围为(　　)A．(－1，0)B．[－1，1]C．(0，1)D．(1，＋∞)
由函数f(x)＝lg (ax2－2x＋a)的定义域为R，所以ax2－2x＋a＞0恒成立，令h(x)＝ax2－2x＋a.
综上，实数a的取值范围为(1，＋∞).
二、 多项选择题5．下列是函数图象的是(　　　)
对于A，若y＝sgn (x)的图象关于y轴对称，则y＝sgn (x)为偶函数，应该满足sgn (－1)＝sgn (1)，但sgn (－1)＝－1，sgn (1)＝1，即sgn (－1)≠sgn (1)，故A错误；
对于B，因为ex＞0，所以对任意x∈R，sgn (ex)＝1，故B正确；
对于D，当x∈(0，1)时，－ln x＞0，y＝x sgn (－ln x)＝x∈(0，1)，当x＝1时，－ln x＝0，y＝x sgn (－ln x)＝0，当x∈(1，＋∞)时，－ln x＜0，y＝x sgn (－ln x)＝－x∈(－∞，－1)，即函数y＝x sgn (－ln x)的值域为(－∞，－1)∪[0，1)，故D正确．
x2－2x＋2(x≥1)
四、 解答题10．(1) 已知函数f(x)的定义域为[－1，5]，求函数f(x－5)的定义域；
因为f(x)的定义域为[－1，5]，所以f(x－5)需满足－1≤x－5≤5，解得4≤x≤10，所以f(x－5)的定义域为[4，10].
(2) 已知函数f(x－1)的定义域是[0，3]，求函数f(x)的定义域；
因为f(x－1)的定义域为[0，3]，所以0≤x≤3，－1≤x－1≤2，所以f(x)的定义域为[－1，2].
10．(3) 若函数f(x)的定义域为[0，1]，求函数g(x)＝f(x＋m)＋f(x－m)(m＞0)的定义域．
B组　滚动小练12．已知函数y＝ln (x2－3x)的定义域为A，集合B＝{x|1≤x≤4}，则(∁RA)∪B等于(　　)A．[0，4]B．(0，4]C．[1，3)D．[1，3]
由题意可知，x2－3x＞0，所以x＜0或x＞3，所以A＝{x|x＜0或x＞3}，故∁RA＝{x|0≤x≤3}．因为B＝{x|1≤x≤4}，所以(∁RA)∪B＝[0，4].
13．(多选)若正整数m，n只有1为公约数，则称m，n互质．对于正整数n，φ(n)是小于或等于n的正整数中与n互质的数的个数，函数φ(n)以其首位研究者欧拉命名，称为欧拉函数，例如：φ(3)＝2，φ(7)＝6，φ(9)＝6，则下列说法正确的有(　　)A．φ(5)＝φ(10)B．φ(2n－1)＝1C．φ(32)＝16D．φ(2n＋2)＞φ(2n)，n是正整数
由题意得φ(5)＝φ(10)＝4，故A正确；当n＝4时，φ(2n－1)＝φ(15)＝8≠1，故B不正确；因为小于或等于32的正整数中与32互质的实数为1，3，5，7，9，11，13，15，17，19，21，23，25，27，29，31，共有16个，所以φ(32)＝16，故C正确；当n＝2时，φ(4)＝φ(6)＝2，故D不正确．
14．已知函数f(x)＝(m＋1)x2－(m－1)x＋m－1.(1) 若不等式f(x)＜1的解集为R，求实数m的取值范围；
根据题意，当m＋1＝0，即m＝－1时，f(x)＝2x－2，不合题意；
14．已知函数f(x)＝(m＋1)x2－(m－1)x＋m－1.(2) 解关于x的不等式f(x)≥(m＋1)x.
f(x)≥(m＋1)x，即(m＋1)x2－2mx＋m－1≥0，即[(m＋1)x－(m－1)](x－1)≥0.①当m＋1＝0，即m＝－1时，解集为{x|x≥1}；