北师大版 (2019)必修 第一册2.2 函数的表示法备课ppt课件

这是一份北师大版 (2019)必修 第一册2.2 函数的表示法备课ppt课件，共44页。PPT课件主要包含了解析式，－11，2图象法等内容，欢迎下载使用。

必备知识·情境导学探新知
1．函数的表示方法有哪几种？2．函数的表示方法各有什么优缺点？如何选择函数的表示方法表示具体问题？3．什么是分段函数？4．分段函数是多个函数吗？5．如何画分段函数的图象？
知识点1　函数的表示法
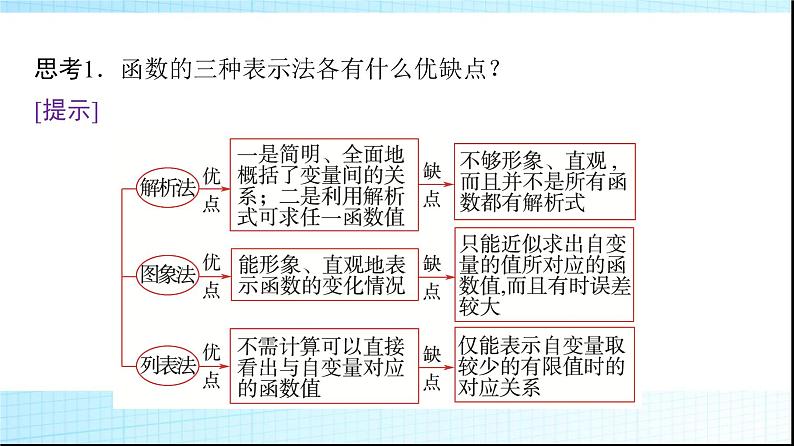
思考1．函数的三种表示法各有什么优缺点？[提示]　
体验1．函数f (x)的图象如图所示，则f (x)的定义域是_________________，值域是________．
体验2．若反比例函数f (x)满足f (3)＝－6，则f (x)的解析式为__________．
[－1，0)∪(0，2]
知识点2　分段函数(1)分段函数如果函数y＝f (x)，x∈A，根据自变量x在A中不同的取值范围，有着不同的对应关系，则称这样的函数为分段函数．(2)分段函数的图象分段函数有几段，它的图象就由几条曲线组成．在同一直角坐标系中，根据每段的定义区间和表达式依次画出图象，要注意每段图象的端点是空心圈还是实心点，组合到一起就得到整个分段函数的图象．
(－∞，0)∪(0，＋∞)
{－2}∪(0，＋∞)
关键能力·合作探究释疑难
类型1　函数的表示法【例1】　某商场新进了10台彩电，每台售价3 000元，试求售出台数x与收款数y之间的函数关系，分别用列表法、图象法、解析法表示出来．
[解]　(1)列表法：
(3)解析法：y＝3 000x，x∈{1，2，3，…，10}．
反思领悟　1．解析法、列表法、图象法是从三个不同角度表示函数的对应关系，同一个函数可用不同的方法表示．2．在用三种方法表示函数时，要注意：(1)解析法要注明函数的定义域；(2)列表法选取的自变量的取值要具有代表性，应能反映定义域的特征；(3)图象法要注意图象是散点还是连续的曲线．
[跟进训练]1．已知函数f (x)，g(x)分别由下表给出．
则f ( g(1))的值为________；当g( f (x))＝2时，x＝________．
1　1　[由于函数关系是用表格形式给出的，知g(1)＝3，∴f (g(1))＝f (3)＝1.由于g(2)＝2，∴f (x)＝2，∴x＝1.]
[解]　(1)当x∈[0，2]时，图象是直线y＝2x＋1的一部分，观察图象可知，其值域为[1，5].
(3)当－2≤x≤2时，图象是抛物线y＝x2＋2x的一部分．由图可得函数的值域是[－1，8].
(4)函数对应图象如图所示：由图可得其值域为(－6，6].
反思领悟　画函数图象的两种常见方法(1)描点法一般步骤：①列表——先找出一些(有代表性的)自变量x，并计算出与这些自变量相对应的函数值f (x)，用表格的形式表示出来；②描点——从表中得到一系列的点(x，f (x))，在坐标平面上描出这些点；③连线——用光滑曲线把这些点按自变量由小到大的顺序连接起来．(2)变换作图法：常用的有水平平移变换、竖直平移变换、翻折变换等．
[解]　(1)因为x∈Z，所以图象为直线y＝1－x上的孤立点，其图象如图①所示．(2)y＝x2－4x＋3＝(x－2)2－1，当x＝1，3时，y＝0；当x＝2时，y＝－1，其图象如图②所示．
类型3　函数解析式的求法方法1　用待定系数法求函数解析式【例3】　(1)已知f (x)是一次函数，且f ( f (x))＝16x－25，求f (x)；(2)已知f (x)是二次函数，且f (x＋1)＋f (x－1)＝2x2－4x，求f (x)．
反思领悟　待定系数法求函数解析式已知函数的类型，如是一次函数、二次函数等，即可设出f (x)的解析式，再根据条件列方程(或方程组)，通过解方程(组)求出待定系数，进而求出函数解析式．
反思领悟　已知f (g(x))＝h(x)求f (x)，常用的两种方法(1)换元法，即令t＝g(x)解出x，代入h(x)中得到一个含t的解析式，即为函数解析式，注意换元后新元的范围．(2)配凑法，即从f (g(x))的解析式中配凑出“g(x)”，即用g(x)来表示h(x)，然后将解析式中的g(x)用x代替即可．
方法3　用方程组法求函数解析式【例5】　已知f (x)＋2f (－x)＝x2＋2x，求f (x)．
[解]　(1)法一：(换元法)　令x＋1＝t，∴x＝t－1，∴f (t)＝3(t－1)＋2＝3t－1，∴f (x)＝3x－1.法二：(配凑法)　f (x＋1)＝3x＋2＝3(x＋1)－1，∴f (x)＝3x－1.
反思领悟　分段函数求值问题的常见解法(1)求分段函数的函数值的方法：先确定要求值的自变量的取值属于哪一段区间，然后代入该段的解析式求值．当出现f ( f (a))的形式时，应从内到外依次求值．(2)已知分段函数的函数值，求自变量的值的方法：先假设自变量的值在分段函数定义域的各段上，然后求出相应自变量的值，切记要检验．(3)在分段函数的前提下，求某条件下自变量的取值范围的方法：先假设自变量的值在分段函数定义域的各段上，然后求出在相应各段定义域上自变量的取值范围，再求它们的并集即可．
A　[f (5)＝f ( f (10))，f (10)＝f ( f (15))＝f (18)＝21，∴f (5)＝f (21)＝24.故选A.]
(－3，1)∪(3，＋∞)　[画出函数f (x)的图象如图所示，令f (x)＝f (1)，得x＝－3，1，3，所以当f (x)>f (1)时，必有x∈(－3，1)∪(3，＋∞)．]
(－3，1)∪(3，＋∞)　
阅读材料·拓展数学大视野
函数图象的变换(探究型)1．函数图象的平移变换函数y＝f (x)的图象与y＝f (x＋a)及y＝f (x)＋a(a≠0)的图象有怎样的关系呢？我们先来看一个例子：作出函数y＝x2，y＝(x＋1)2，y＝x2－1的图象，观察它们之间有怎样的关系．
在同一平面直角坐标系中，它们的图象如图所示．
观察图象可知，y＝(x＋1)2的图象可由y＝x2的图象向左平移1个单位长度得到；y＝x2－1的图象可由y＝x2的图象向下平移1个单位长度得到．由此得到如下规律：(1)函数y＝f (x＋a)的图象是由函数y＝f (x)的图象沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位长度得到的，即“左加右减”；(2)函数y＝f (x)＋a的图象是由函数y＝f (x)的图象沿y轴方向向上(a>0)或向下(a<0)平移|a|个单位长度得到的，即“上加下减”．
在不同的平面直角坐标系中，分别作出y＝|x2－2x－3|与y＝x2－2|x|－3的图象，如图(1)(2)所示．
通过观察两个图象可知，y＝|x2－2x－3|的图象可由y＝x2－2x－3的图象经过下列变换得到：保持y＝x2－2x－3的图象在x轴上方的部分不变，将x轴下方的部分沿x轴翻折上去，即可得到y＝|x2－2x－3|的图象．y＝x2－2|x|－3的图象可由y＝x2－2x－3的图象经过下列变换得到：保持y＝x2－2x－3的图象在y轴上及其右侧的部分不变，y轴左侧的图象换成将y轴右侧的图象沿y轴翻折而成的图象，则这两部分就构成了y＝x2－2|x|－3的图象．
(1)　　　　　 　　　(2)
由此可得如下规律：(1)要作y＝| f (x)|的图象，可先作y＝f (x)的图象，然后将x轴上及其上方的部分保持不变，x轴下方的部分沿x轴对称地翻折上去即可．(2)要作y＝f (|x|)的图象，可先作y＝f (x)的图象，然后将y轴上及其右侧的图象不动，y轴左侧的图象换成将y轴右侧的图象沿y轴翻折而成的图象即可．
学习效果·课堂评估夯基础
1．已知函数f (x)由下表给出，则f (3)等于(　　)
A．1 　B．2 C．3 　D．不存在
2．某学生离家去学校，一开始跑步前进，跑累了再走余下的路程．下列图中纵轴表示离校的距离，横轴表示出发后的时间，则较符合该学生走法的是(　　)
A　　　　B　　　　C　　　　DD　[由题意可知，一开始速度较快，后来速度变慢，所以开始曲线比较陡峭，后来曲线比较平缓，又纵轴表示离校的距离，所以开始时距离最大，最后距离为0.]
3．函数y＝|x＋1|的图象是(　　)
A　　　 　B　 　　　C　 　 　D
4．如果一次函数f (x)的图象过点(1，0)及点(0，1)，则f (3)＝___．