

2022-2023学年广东省深圳市宝安区八年级(上)期末数学试卷
展开1.(3分)下列各数中,是无理数的是( )
A.B.0.C.D.
2.(3分)二元一次方程x﹣2y=3有无数多个解,下列四组值中不是该方程的解是( )
A.B.C.D.
3.(3分)下列式子正确的是( )
A.B.C.D.
4.(3分)将一副直角三角板如图放置,已知∠F=45°,∠B=60°,EF∥BC,则∠BGE的度数为( )
A.115°B.105°C.110°D.120°
5.(3分)下列各组数中,能作为直角三角形三边的是( )
A.1,2,B.3,3,6C.4,6,8D.,,
6.(3分)下列命题中是真命题的是( )
A.无限小数都是无理数 B.数轴上的点表示的数都是有理数
C.一个三角形的最大内角不会小于60° D.同旁内角互补
7.(3分)某配餐公司需用甲、乙两种食材为在校午餐的同学配置营养餐,两种食材的蛋白质含量和碳水化合物含量如下表所示:
若每位中学生每餐需要21单位蛋白质和40单位碳水化合物,那么每餐甲、乙两种食材各多少克恰好满足一个中学生的需要?设每餐需要甲食材x克,乙食材y克,那么可列方程组为( )
A. B. C. D.
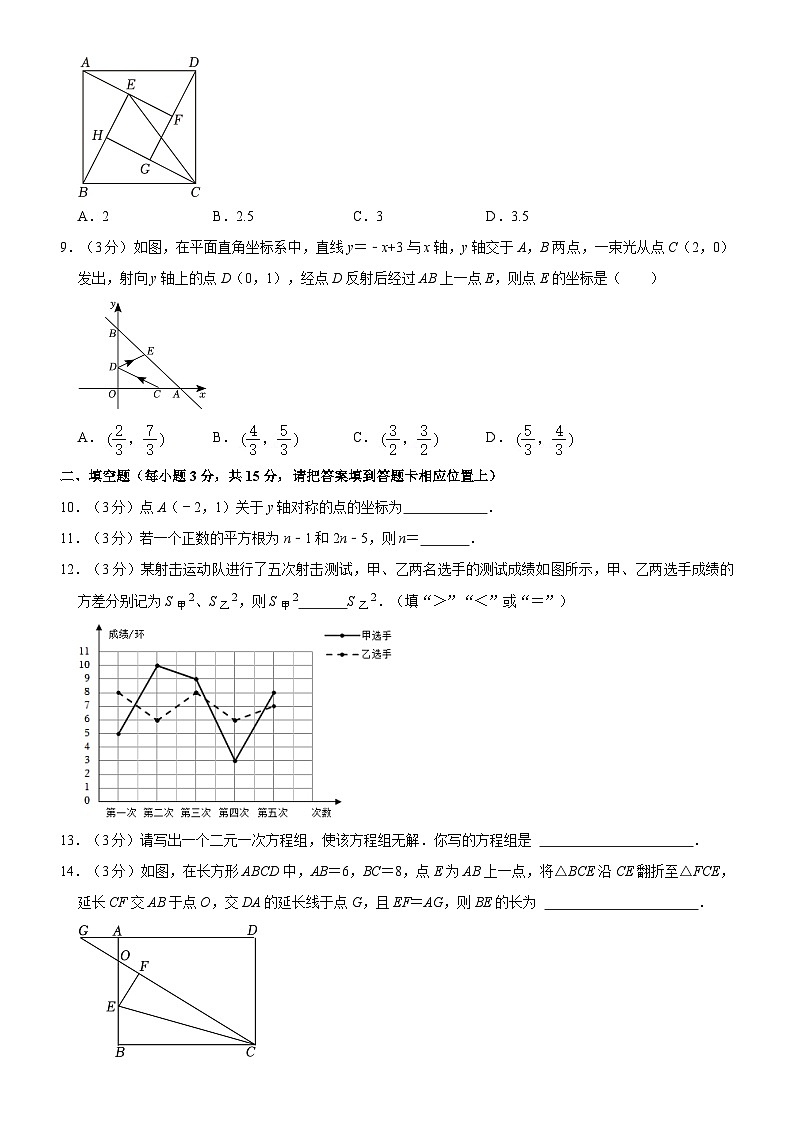
8.(3分)如图是我国古代著名的“赵爽弦图”,大正方形ABCD是由四个全等的直角三角形和一个小正方形拼接而成,连接EC,若正方形ABCD的面积为10,EC=BC,则小正方形EFGH的面积为( )
A.2B.2.5C.3D.3.5
9.(3分)如图,在平面直角坐标系中,直线y=﹣x+3与x轴,y轴交于A,B两点,一束光从点C(2,0)发出,射向y轴上的点D(0,1),经点D反射后经过AB上一点E,则点E的坐标是( )
A.B.C.D.
二、填空题(每小题3分,共15分,请把答案填到答题卡相应位置上)
10.(3分)点A(﹣2,1)关于y轴对称的点的坐标为 .
11.(3分)若一个正数的平方根为n﹣1和2n﹣5,则n= .
12.(3分)某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为S甲2、S乙2,则S甲2 S乙2.(填“>”“<”或“=”)
13.(3分)请写出一个二元一次方程组,使该方程组无解.你写的方程组是 .
14.(3分)如图,在长方形ABCD中,AB=6,BC=8,点E为AB上一点,将△BCE沿CE翻折至△FCE,延长CF交AB于点O,交DA的延长线于点G,且EF=AG,则BE的长为 .
三、解答题(本题共7小题,其中第16题8分,第17题6分,第18题8分,第19题8分,第20题8分,第21题8分,第22题9分,共55分)
15.(8分)计算题:
(1); (2).
16.(6分)解方程组.
17.(8分)2022年11月5日,第二十三届深圳读书月盛大开幕,本届读书月以“读时代新篇创文明典范”为年度主题,2300余场文化活动“阅”动全城.春海学校积极响应深圳读书月的号召,在校内推广课外阅读活动.为了解七、八年级学生每周课外阅读的情况,分别从两个年级随机抽取了10名学生进行调查,并对调查数据进行整理分析.现将参与调查的每个学生每周课外阅读的时间用x(小时)表示,并将两个年级的调查数据分别分成四组:A.0≤x<4,B.4≤x<8,C.8≤x<12,D.12≤x≤16,以下是相关的数据信息:
七年级学生调查数据:3,14,8,9,9,11,8,11,16,11
八年级学生调查数据位于C组中的是:9,10,10,10
七、八年级抽取的学生每周课外阅读时间统计表
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= ,c= ;
(2)若七、八年级共有1000名学生,请你估计该校七、八年级学生每周课外阅读时间不低于12小时的共有 人.
18.(8分)列方程解应用题:某校举行了“歌唱祖国,爱我中华”合唱比赛,学校购买了A,B两种型号的笔记本对表现优异的班级进行奖励.若购买40本B型笔记本比20本A型笔记本多20元,购买30本A型笔记本和50本B型笔记本价格相同,请计算A,B两种笔记本的单价分别是多少元?
19.(8分)如图,在△ABC中,过点B作BD⊥CA交CA的延长线于点D,过点C作CE⊥BA交BA的延长线于点E,延长BD,CE相交于点F,BF=AC=.
(1)求证:△BEF≌△CEA;
(2)若CE=2,求BD的长.
20.(8分)学校饮用水安全问题事关重大,直接影响到广大青少年的身体健康.为了全力保障校园饮水安全,让学生喝上放心水、健康水,星月学校在教学楼每个楼层都安装了饮水机.为了解饮水机的使用情况,小亮所在综合实践小组进行了调查研究,他们发现:饮水机的容量是25L,共有三个放水管,且每个水管出水的速度相同;三个水管同时打开时,饮水机的存水量(升)与放水时间(分)的关系如表所示.
(1)当三个放水管全部打开时,每分钟的总出水量为 L.
(2)某天课间休息时,同学们依次用饮水机接水.假设前后两人接水的间隔时间忽略不计,且水不发生泼洒,每个同学所接的水量相同.刚开始时,只打开了其中两个放水管,过了一会儿,来接水的同学越来越多,三个放水管全部打开.饮水机的存水量y(L)与放水时间x(min)的函数关系如图所示.
①求饮水机中的存水量y(L)与放水时间x(min)(x≥3)的函数关系式;
②如果前3分钟恰好有10名同学接完水,则前25个同学接完水共需多少时间?
21.(9分)点P、点P′和点Q为平面直角坐标系中的三个点,给出如下定义:若PQ=P′Q,且∠PQP′=90°,则称P′为点P关于点Q的等垂点.
(1)已知点Q的坐标为(4,0),
①如图1,若点P为原点,直接写出P关于Q的等垂点P′的坐标 ;
②如图2,P为y轴上一点,且点P关于点Q的等垂点P′恰好在一次函数y=2x+3的图象上,求点P′的坐标;
(2)如图3,若点Q的坐标为(1,﹣2),P为直线y=2上一点,P关于点Q的等垂点P′位于y轴右侧,连接OP′,QP′,请问OP′+QP′是否有最小值?若有,请求出最小值;若无,请说明理由.
2022-2023学年广东省深圳市宝安区八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(共9小题,每小题3分,共30分,每小题有四个选项,其中只有一个是正确的,请把答案按要求填涂到答题卡相应位置上)
1.(3分)下列各数中,是无理数的是( )
A.B.0.C.D.
【答案】D
【分析】根据无理数的定义逐一判断,即可解答.
【解答】解:A、∵=2,
∴是有理数,
故A不符合题意;B、0.是有理数,故B不符合题意;C、是有理数,故C不符合题意;
D、是无理数,故D符合题意;
故选:D.
2.(3分)二元一次方程x﹣2y=3有无数多个解,下列四组值中不是该方程的解是( )
A.B.C.D.
【答案】B
【分析】将各项中x与y的值代入方程检验即可.
【解答】解:A、当x=1,y=﹣1时,x﹣2y=1﹣2×(﹣1)=3,是方程的解,不合题意;
B、当x=﹣1,y=﹣3时,x﹣2y=﹣1﹣2×(﹣3)=5,不是方程的解,符合题意;
C、当x=5,y=1时,x﹣2y=5﹣2×1=3,是方程的解,不合题意;
D、当x=﹣1,y=﹣2时,x﹣2y=﹣1﹣2×(﹣2)=3,是方程的解,不合题意;
故选:B.
3.(3分)下列式子正确的是( )
A.B.C.D.
【答案】C
【分析】根据二次根式的加法,减法,乘法法则,二次根式的性质进行计算,逐一判断即可解答.
【解答】解:A、=2,故A不符合题意;
B、与不能合并,故B不符合题意;
C、×=2,故C符合题意;
D、2﹣=,故D不符合题意;
故选:C.
4.(3分)将一副直角三角板如图放置,已知∠F=45°,∠B=60°,EF∥BC,则∠BGE的度数为( )
A.115°B.105°C.110°D.120°
【答案】B
【分析】根据两直线平行,内错角相等得出∠GDB=45°,进而利用三角形外角性质解答即可.
【解答】解:∵EF∥BC,
∴∠GDB=∠E=45°,
∴∠BGE=∠B+∠GDB=60°+45°=105°,
故选:B.
5.(3分)下列各组数中,能作为直角三角形三边的是( )
A.1,2,B.3,3,6C.4,6,8D.,,
【答案】A
【分析】根据勾股定理的逆定理进行计算,逐一判断即可解答.
【解答】解:A、∵12+()2=4,22=4,
∴12+()2=22,
∴能组成直角三角形,
故A符合题意;
B、∵3+3=6,
∴不能组成三角形,
故B不符合题意;
C、∵42+62=52,82=64,
∴42+62≠82,
∴不能组成直角三角形,
故C不符合题意;
D、∵()2+()2=,()2=,
∴()2+()2≠()2,
∴不能组成直角三角形,
故D不符合题意;
故选:A.
6.(3分)下列命题中是真命题的是( )
A.无限小数都是无理数
B.数轴上的点表示的数都是有理数
C.一个三角形的最大内角不会小于60°
D.同旁内角互补
【答案】C
【分析】根据有理数、平行线的性质、三角形的内角、无理数的概念判断即可.
【解答】解:A、无限不循环小数都是无理数,故本选项说法是假命题,不符合题意;
B、数轴上的点表示的数都是实数,故本选项说法是假命题,不符合题意;
C、一个三角形的最大内角不会小于60°,是真命题,符合题意;
D、两直线平行,同旁内角互补,故本选项说法是假命题,不符合题意;
故选:C.
7.(3分)某配餐公司需用甲、乙两种食材为在校午餐的同学配置营养餐,两种食材的蛋白质含量和碳水化合物含量如下表所示:
若每位中学生每餐需要21单位蛋白质和40单位碳水化合物,那么每餐甲、乙两种食材各多少克恰好满足一个中学生的需要?设每餐需要甲食材x克,乙食材y克,那么可列方程组为( )
A.B.C.D.
【答案】C
【分析】根据题意和表格中的数据,可以列出方程组,从而可以判断哪个选项符合题意.
【解答】解:由题意可得,
,
故选:C.
8.(3分)如图是我国古代著名的“赵爽弦图”,大正方形ABCD是由四个全等的直角三角形和一个小正方形拼接而成,连接EC,若正方形ABCD的面积为10,EC=BC,则小正方形EFGH的面积为( )
A.2B.2.5C.3D.3.5
【答案】A
【分析】设正方形EFGH的边长为a,用a表示四个全等的直角三角形和一个小正方形的面积,由正方形ABCD的面积为10,建立方程求a.
【解答】解:∵四边形EFGH是正方形,
∴CH⊥BE,
∵EC=BC,
∴HE=HB,
∴BE=2HE,
∴HC=2HE,
设正方形EFGH的边长为a,则HB=HE=a,HC=2a,
∴S正方形ABCD=S正方形EFGH+4S△BHC=a2+4××HB•HC=a2+4××a•2a=5a2=10,
∴a2=2,
故选:A.
9.(3分)如图,在平面直角坐标系中,直线y=﹣x+3与x轴,y轴交于A,B两点,一束光从点C(2,0)发出,射向y轴上的点D(0,1),经点D反射后经过AB上一点E,则点E的坐标是( )
A.B.C.D.
【答案】B
【分析】在D上方取点F,使DF=OD=1,过F作FG⊥y轴交DE延长线于G,证明△FDG≌△ODC(AAS),可求出G(2,2),直线DG函数表达式为y=x+1,联立,解得E(,).
【解答】解:在D上方取点F,使DF=OD=1,过F作FG⊥y轴交DE延长线于G,如图:
由反射定律可得,∠EDF=∠CDO,
∵OD=DF.∠DFG=90°=∠AOD,
∴△FDG≌△ODC(AAS),
∴FG=OC=2,
∴G(2,2),
由G(2,2),D(0,1)得直线DG函数表达式为y=x+1,
联立,解得,∴E(,),
故选:B.
二、填空题(每小题3分,共15分,请把答案填到答题卡相应位置上)
10.(3分)点A(﹣2,1)关于y轴对称的点的坐标为 (2,1) .
【答案】见试题解答内容
【分析】根据平面直角坐标系关于坐标轴成轴对称的两点的坐标之间的关系,易得答案.
【解答】解:根据平面内关于y轴对称的点,纵坐标相同,横坐标互为相反数,
已知点A(﹣2,1),则点A关于y轴对称的点的横坐标为﹣(﹣2)=2,纵坐标为1,
故点(﹣2,1)关于y轴对称的点的坐标是(2,1).
故答案为(2,1).
11.(3分)若一个正数的平方根为n﹣1和2n﹣5,则n= 2 .
【答案】2.
【分析】根据一个正数的平方根有两个且互为相反数列出方程,求出n的值即可.
【解答】解:∵一个正数的平方根为n﹣1和2n﹣5,
∴n﹣1+2n﹣5=0,
解得:n=2.
故答案为:2.
12.(3分)某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图所示,甲、乙两选手成绩的方差分别记为S甲2、S乙2,则S甲2 > S乙2.(填“>”“<”或“=”)
【答案】>.
【分析】直接根据图表数据的波动大小进行判断即可.
【解答】解:图表数据可知,
甲数据偏离平均数数据较大,乙数据偏离平均数数据较小,
即甲的波动性较大,即方差大,
故答案为:>.
13.(3分)请写出一个二元一次方程组,使该方程组无解.你写的方程组是 (答案不唯一) .
【分析】根据二元一次方程组的定义,结合方程组的解即可得到结论.
【解答】解:根据二元一次方程组的定义,结合方程组无解得,
14.(3分)如图,在长方形ABCD中,AB=6,BC=8,点E为AB上一点,将△BCE沿CE翻折至△FCE,延长CF交AB于点O,交DA的延长线于点G,且EF=AG,则BE的长为 .
【答案】.
【分析】由折叠可知∠B=∠CFE=90°,BE=EF,BC=CF=8,易通过AAS证明△EFO≌△GAO,得到OF=OA,OE=OG,于是AE=FG,设BE=x,则EF=AG=x,AE=FG=6﹣x,进而可得DG=8+x,CG=14﹣x,在Rt△CDG中,利用勾股定理建立方程,求解即可.
【解答】解:∵四边形ABCD为矩形,AB=6,BC=8,
∴AB=CD=6,BC=AD=8,∠B=∠D=90°,
由折叠可知,∠B=∠CFE=90°,BE=EF,BC=CF=8,
∴∠EFO=90°=∠GAO,
在△EFO和△GAO中,
,
∴△EFO≌△GAO(AAS),
∴OF=OA,OE=OG,
∴OF+OG=OA+OE,即AE=FG,
设BE=x,则EF=AG=x,AE=FG=AB﹣BE=6﹣x,
∴DG=AD+AG=8+x,CG=CF+FG=8+6﹣x=14﹣x,
在Rt△CDG中,CD2+DG2=CG2,
∴62+(8+x)2=(14﹣x)2,
解得:x=,
∴BE=.
故答案为:.
三、解答题(本题共7小题,其中第16题8分,第17题6分,第18题8分,第19题8分,第20题8分,第21题8分,第22题9分,共55分)
15.(8分)计算题:
(1);
(2).
【答案】(1)3;
(2)4﹣3.
【分析】(1)原式第一项分母有理化,第二项利用平方差公式化简,计算即可求出值;
(2)原式利用二次根式性质,零指数幂,立方根定义,以及绝对值的代数意义计算即可求出值.
【解答】解:(1)原式=+5﹣4
=2+5﹣4
=3;
(2)原式=3+1﹣3+﹣1
=4﹣3.
16.(6分)解方程组.【答案】.
【分析】利用加减消元法解方程组即可.
【解答】解:原方程组化为,
①﹣②得:x=4,
将x=4代入②得:4﹣y=1,
解得:y=3,故原方程组的解为.
17.(8分)2022年11月5日,第二十三届深圳读书月盛大开幕,本届读书月以“读时代新篇创文明典范”为年度主题,2300余场文化活动“阅”动全城.春海学校积极响应深圳读书月的号召,在校内推广课外阅读活动.为了解七、八年级学生每周课外阅读的情况,分别从两个年级随机抽取了10名学生进行调查,并对调查数据进行整理分析.现将参与调查的每个学生每周课外阅读的时间用x(小时)表示,并将两个年级的调查数据分别分成四组:A.0≤x<4,B.4≤x<8,C.8≤x<12,D.12≤x≤16,以下是相关的数据信息:
七年级学生调查数据:3,14,8,9,9,11,8,11,16,11
八年级学生调查数据位于C组中的是:9,10,10,10
七、八年级抽取的学生每周课外阅读时间统计表
根据以上信息,解答下列问题:
(1)上述图表中a= 11 ,b= 10 ,c= 9.5 ;
(2)若七、八年级共有1000名学生,请你估计该校七、八年级学生每周课外阅读时间不低于12小时的共有 200 人.
【答案】(1)11,10,9.5;
(2)200人.
【分析】(1)分别根据众数和中位数的定义解答即可;
(2)用1000乘样本中每周课外阅读时间不低于12小时所占比例即可.
【解答】解:(1)七年级10名学生数据中,11出现的次数最多,故众数a=11,
把七年级10名学生数据从小到大排列,排在中间的两个数分别为9、11,故中位数b==10,
把八年级10名学生数据从小到大排列,排在中间的两个数分别为9、10中位数b==9.5,
故答案为:11,10,9.5;
(2)1000×=200(人),
即估计该校七、八年级学生每周课外阅读时间不低于12小时的大约共有200人.
故答案为:200.
18.(8分)列方程解应用题:某校举行了“歌唱祖国,爱我中华”合唱比赛,学校购买了A,B两种型号的笔记本对表现优异的班级进行奖励.若购买40本B型笔记本比20本A型笔记本多20元,购买30本A型笔记本和50本B型笔记本价格相同,请计算A,B两种笔记本的单价分别是多少元?
【答案】A型笔记本的单价为5元,B型笔记本的单价为3元.
【分析】设A型笔记本的单价为x元,B型笔记本的单价为y元,由“若购买40本B型笔记本比20本A型笔记本多20元,购买30本A型笔记本和50本B型笔记本价格相同”,列出二元一次方程组,解方程组即可.
【解答】解:设A型笔记本的单价为x元,B型笔记本的单价为y元,
由题意得:,
解得:,
答:A型笔记本的单价为5元,B型笔记本的单价为3元.
19.(8分)如图,在△ABC中,过点B作BD⊥CA交CA的延长线于点D,过点C作CE⊥BA交BA的延长线于点E,延长BD,CE相交于点F,BF=AC=.
(1)求证:△BEF≌△CEA;
(2)若CE=2,求BD的长.
【答案】(1)证明见解答过程;
(2)BD的长为.
【分析】(1)由CE⊥BA,得∠BEF=90°=∠AEC,又BD⊥CA,∠DAB=∠EAC,可得∠ABD=∠ACE,即∠EBF=∠ACE,根据AAS即可证明△BEF≌△CEA;
(2)由△BEF≌△CEA,得BE=CE=2,利用勾股定理得BC==2,EF==1,利用BC2﹣BD2=CD2=CF2﹣DF2,可得(2)2﹣BD2=32﹣(﹣BD)2,即可解得答案.
【解答】(1)证明:∵CE⊥BA,
∴∠BEF=90°=∠AEC,
∵BD⊥CA,
∴∠ADB=90°=∠AEC,
∵∠DAB=∠EAC,
∴∠ABD=∠ACE,即∠EBF=∠ACE,
在△BEF和△CEA中,
,
∴△BEF≌△CEA(AAS);
(2)解:由(1)知△BEF≌△CEA,
∴BE=CE=2,
∴BC===2,EF===1,
∴CF=CE+EF=2+1=3;
∵BC2﹣BD2=CD2=CF2﹣DF2,
∴BC2﹣BD2=CF2﹣(BF﹣BD)2,
∴(2)2﹣BD2=32﹣(﹣BD)2,
解得BD=;
∴BD的长为.
20.(8分)学校饮用水安全问题事关重大,直接影响到广大青少年的身体健康.为了全力保障校园饮水安全,让学生喝上放心水、健康水,星月学校在教学楼每个楼层都安装了饮水机.为了解饮水机的使用情况,小亮所在综合实践小组进行了调查研究,他们发现:饮水机的容量是25L,共有三个放水管,且每个水管出水的速度相同;三个水管同时打开时,饮水机的存水量(升)与放水时间(分)的关系如表所示.
(1)当三个放水管全部打开时,每分钟的总出水量为 2.5 L.
(2)某天课间休息时,同学们依次用饮水机接水.假设前后两人接水的间隔时间忽略不计,且水不发生泼洒,每个同学所接的水量相同.刚开始时,只打开了其中两个放水管,过了一会儿,来接水的同学越来越多,三个放水管全部打开.饮水机的存水量y(L)与放水时间x(min)的函数关系如图所示.
①求饮水机中的存水量y(L)与放水时间x(min)(x≥3)的函数关系式;
②如果前3分钟恰好有10名同学接完水,则前25个同学接完水共需多少时间?
【答案】(1)2.5;
(2)①y=﹣2.5x+27.5(3≤x≤11);
②前25个同学接完水共需多6min.
【分析】(1)由表列出算式计算即可;
(2)①求出打开其中两个放水管,当x=3时,饮水机的存水量y=25﹣×3=20(L),再用待定系数法可得饮水机中的存水量y与放水时间x的函数关系式为y=﹣2.5x+27.5(3≤x≤11);
②求出每个同学接水=0.5(L),可知前25个同学共接水0.5×25=12.5(L),此时饮水机中的存水量y=25﹣12.5=12.5,故12.5=﹣2.5x+27.5,即可解得答案.
【解答】解:(1)由表可知,当三个放水管全部打开时,每分钟的总出水量为=2.5(L),
故答案为:2.5;
(2)①根据题意知,打开其中两个放水管,每分钟的总出水量为×2=(L),
∴当x=3时,饮水机的存水量y=25﹣×3=20(L),
当x≥3时,设y=kx+b,把(3,20),(5,15)代入得:
,
解得,
∴饮水机中的存水量y与放水时间x的函数关系式为y=﹣2.5x+27.5(3≤x≤11);
②∵前3分钟恰好有10名同学接完水,
∴每个同学接水=0.5(L),
∴前25个同学共接水0.5×25=12.5(L),
此时饮水机中的存水量y=25﹣12.5=12.5,
∴12.5=﹣2.5x+27.5,
解得x=6,
∴前25个同学接完水共需多6min.
21.(9分)点P、点P′和点Q为平面直角坐标系中的三个点,给出如下定义:若PQ=P′Q,且∠PQP′=90°,则称P′为点P关于点Q的等垂点.
(1)已知点Q的坐标为(4,0),
①如图1,若点P为原点,直接写出P关于Q的等垂点P′的坐标 (4,4)或(4,﹣4) ;
②如图2,P为y轴上一点,且点P关于点Q的等垂点P′恰好在一次函数y=2x+3的图象上,求点P′的坐标;
(2)如图3,若点Q的坐标为(1,﹣2),P为直线y=2上一点,P关于点Q的等垂点P′位于y轴右侧,连接OP′,QP′,请问OP′+QP′是否有最小值?若有,请求出最小值;若无,请说明理由.
【答案】(1)①(4,4)或(4,﹣4);②(﹣,﹣4)或(,4);(2)OP′+QP′有最小值,最小值为.
【分析】(1)①利用等垂点的定义,画出图形解答即可;
②利用分类讨论的思想方法分两种情形解答:Ⅰ.当点P在y轴的正半轴上时,过点P′作P′A⊥x轴于点A,设P′(m,2m+3),则P′A=﹣2m﹣3,利用全等三角形的判定与性质得到AP′=OQ=4,则﹣2m﹣3=4,求得m值,则结论可得;Ⅱ.当点P在y轴的正半轴上时,过点P′作P′B⊥x轴于点B,利用Ⅰ中的方法解答即可得出结论;
(2)过点Q作平行于x轴的直线a,交y轴于点B,过点P作PC⊥a于点C,交x轴于点A,过点P′作P′D⊥a于点D,利用全等三角形的判定与性质得到PC=QD=4,则BD=BQ+QD=1+4=5,于是得到点P′的横坐标为5,即点P′在直线x=5上运动,再利用将军饮马模型解答即可得出结论.
【解答】解:(1)①作出点P关于点Q的等垂点,如图,
则P′Q=PQ,
∵点Q的坐标为(4,0),若点P为原点,
∴PQ=4,
∴P′Q=PQ=4,
∵P′Q⊥x轴,
∴P关于Q的等垂点P′的坐标为(4,4)或(4,﹣4).
故答案为:(4,4)或(4,﹣4);
②Ⅰ.当点P在y轴的正半轴上时,过点P′作P′A⊥x轴于点A,如图,
∵P′恰好在一次函数y=2x+3的图象上,
∴设P′(m,2m+3),
∴P′A=﹣2m﹣3,
∵点Q的坐标为(4,0),
∴OQ=4.
∵PQ⊥P′Q,
∴∠PQA+∠AQP′=90°,
∵∠AQP′+∠AP′Q=90°,
∴∠AP′Q=∠OQP.
在△AP′Q和△OQP中,
,
∴△AP′Q≌△OQP(AAS),
∴AP′=OQ=4,
∴﹣2m﹣3=4,
∴m=﹣,
∴P′(﹣,﹣4);
Ⅱ.当点P在y轴的负半轴上时,过点P′作P′B⊥x轴于点B,如图,
∵P′恰好在一次函数y=2x+3的图象上,
∴设P′(m,2m+3),
∴P′B=2m+3,
同Ⅰ可得:△P′BQ≌△QOP,
∴P′B=OQ=4,
∴2m+3=4,
∴m=,
∴P′(,4).
综上,点P′的坐标为(﹣,﹣4)或(,4);
(3)OP′+QP′有最小值,最小值为,理由:
过点Q作平行于x轴的直线a,交y轴于点B,过点P作PC⊥a于点C,交x轴于点A,过点P′作P′D⊥a于点D,如图,
则OB=2,BQ=1,PA=2,AC=OB=2,
∴PC=PA+AC=4.
∵∠CPQ+∠CQP=90°,∠CQP+∠P′QD=90°,
∴∠CPQ=∠DQP′.
在△PCQ和△QDP′中,
,
∴△PCQ≌△QDP′(AAS),
∴PC=QD=4,
∴BD=BQ+QD=1+4=5,
∴点P′的横坐标为5,即点P′在直线x=5上运动,
作点O关于直线x=5的对称点O′,连接O′Q,交直线x=5于点P″,
则P″O=P″O′,
∴当点P′与点P″重合时,且Q,P″,O′在一条直线上时,OP′+QP′的值最小,最小值为O′Q.
过点Q作QE⊥OO′于点E,则OE=1,QE=2,
∴O′E=OO′﹣OE=10﹣1=9,
∴O′Q===.
∴OP′+QP′有最小值,最小值为.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2023/12/30 19:40:40;用户:初中数学;邮箱:zqxdwh@xyh.cm;学号:37246586
菁优网APP 菁优网公众号 菁优网小程序甲食材
乙食材
每克所含蛋白质
0.3单位
0.7单位
每克所含碳水化合物
0.6单位
0.4单位
平均数
众数
中位数
七年级
10
a
b
八年级
9
10
c
放水时间(分)
0
3
8
…
直饮水机的存水量(升)
25
17.5
5
…
甲食材
乙食材
每克所含蛋白质
0.3单位
0.7单位
每克所含碳水化合物
0.6单位
0.4单位
平均数
众数
中位数
七年级
10
a
b
八年级
9
10
c
放水时间(分)
0
3
8
…
直饮水机的存水量(升)
25
17.5
5
…
2022-2023学年广东省深圳市宝安区八年级(下)期末数学试卷(含解析 ): 这是一份2022-2023学年广东省深圳市宝安区八年级(下)期末数学试卷(含解析 ),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省深圳市宝安区七年级(上)期末数学试卷(含解析): 这是一份2022-2023学年广东省深圳市宝安区七年级(上)期末数学试卷(含解析),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省深圳市宝安区新安中学八年级(上)期中数学试卷(含解析): 这是一份2022-2023学年广东省深圳市宝安区新安中学八年级(上)期中数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












