黑龙江省鸡西市2023-2024学年八年级下学期期末数学试卷(含答案)

这是一份黑龙江省鸡西市2023-2024学年八年级下学期期末数学试卷(含答案)，共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。


一、单选题
1．下列计算正确的是( )
A.B.
C.D.
2．以下列各组数为三角形的边长,能构成直角三角形的是( )
A.1,2,3B.2,3,4C.6,8,10D.5,12,9
3．一次函数的图象经过的象限是( )
A.一、二、三B.二、三、四C.一、二、四D.一、三、四
4．某射击队进行1000射击比赛,每人射击10次,经过统计,甲、乙两名队员成绩如下：平均成绩都是96.2环,甲的方差是0.25,乙的方差是0.21,下列说法正确的是( )
A.甲的成绩比乙稳定B.乙的成绩比甲稳定
C.甲乙成绩稳定性相同D.无法确定谁稳定
5．对于一次函数,下列结论中正确的是( )
A.函数的图象与x轴交点坐标是
B.函数的图象不经过第四象限
C.函数的图象向上平移2个单位长度得到函数的图象
D.函数值随自变量的增大而减小
6．如图,延长矩形的边至点E,使,连接,若,那么的度数是( )
A.B.C.D.
7．两个一次函数和在同一平面直角坐标系中的图象可能是( )
A.B.
C.D.
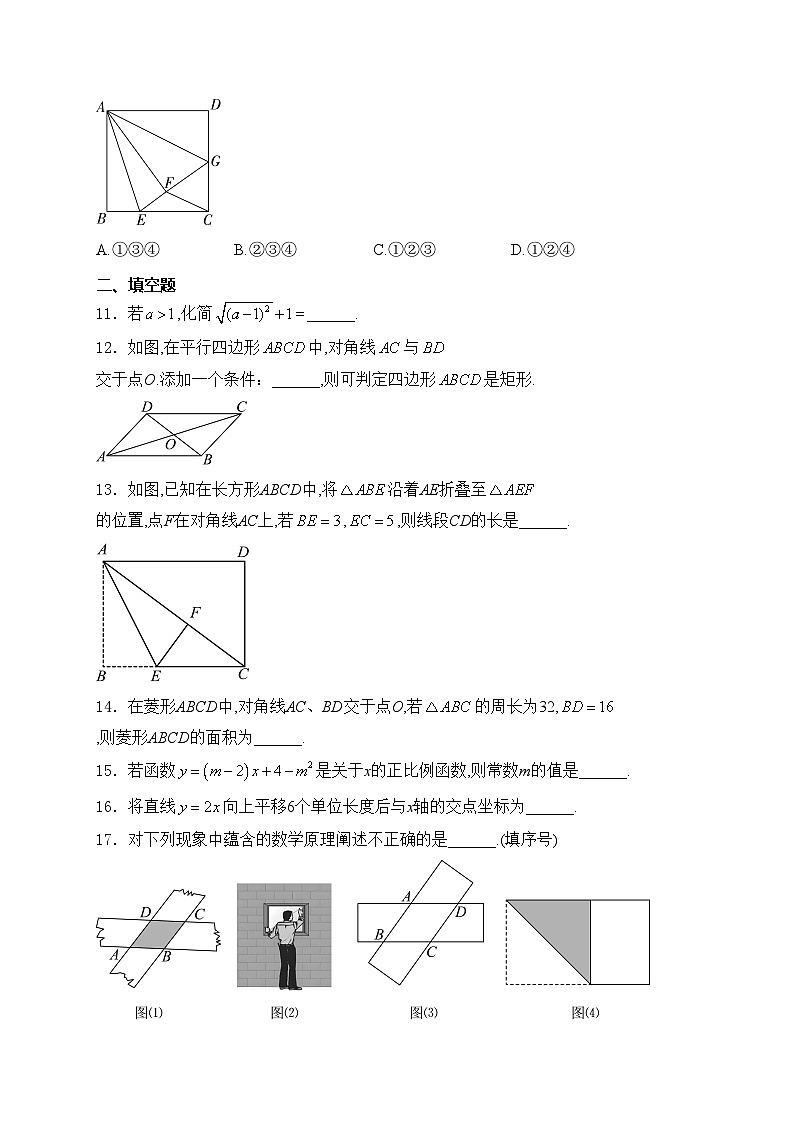
8．如图所示,若一次函数(、均为实数,且)和一次函数(、均为实数,且)的图象的交点的横坐标为,则关于x的不等式的解集是( )
A.B.C.D.
9．如图,AC是菱形ABCD的对角线,P是AC上一个动点,过点P分别作AB、BC的垂线,垂足分别是F和E.若菱形ABCD的周长是12cm,面积是,则的值是( )
A.1.5B.1C.2D.4
10．如图,在正方形中,E是边上一点,,,将正方形边沿折叠到,延长交于G,连接,现在有如下四个结论：①；②；③；④.其中结论正确的选项是( )
A.①③④B.②③④C.①②③D.①②④
二、填空题
11．若,化简______.
12．如图,在平行四边形中,对角线与交于点O.添加一个条件：______,则可判定四边形是矩形.
13．如图,已知在长方形ABCD中,将沿着AE折叠至的位置,点F在对角线AC上,若,,则线段CD的长是______.
14．在菱形ABCD中,对角线AC、BD交于点O,若的周长为32,,则菱形ABCD的面积为______.
15．若函数是关于x的正比例函数,则常数m的值是______.
16．将直线向上平移6个单位长度后与x轴的交点坐标为______.
17．对下列现象中蕴含的数学原理阐述不正确的是______.(填序号)
①如图(1),剪两张对边平行的纸条,随意交叉叠放在一起,重合的部分构成一个平行四边形,其依据是两组对边分别平行的四边形是平行四边形.
②如图(2),工人师傅在做矩形门窗时,不仅测量出两组对边的长度是否相等,还要测量出两条对角线的长度相等,以确保图形是矩形,其依据是对角线相等的四边形是矩形.
③如图(3),将两张等宽的纸条放在一起,重合部分构成的四边形一定是菱形,其依据是一组邻边相等的平行四边形是菱形.
④如图(4),把一张长方形纸片按如图方式折一下,就可以裁出正方形,其依据是一组邻边相等的矩形是正方形.
18．如图,在边长为2的正方形中,E,F分别是,上的动点,M,N分别是,的中点,则的最大值为______.
19．菱形ABCD中,,,点P是菱形ABCD内一点,,则AP的长为______.
20．如图,矩形的面积为,对角线交于点O,以、为邻边作平行四边形,对角线交于点,以,为邻边作平行四边形……依此类推,则平行四边形的面积为______.
三、解答题
21．计算：
(1)；
(2).
22．如图,已知一条直线上三个点,其坐标分别是,,,直线与x轴相交于点A,与y轴相交于点B.
(1)求n的值；
(2)若在y轴上有一点P,使,求的面积.
23．大年初一上映两部喜剧片《热辣滚烫》和《飞驰人生》,为了解学生对这两部影片的评价,某调查小组从该校八年级学生中随机抽取了20名学生对这两部作品分别进行打分(满分10分),并进行整理、描述和分析,下面给出了部分信息.
《飞驰人生2》得分情况：
7,8.7,10.7,6,9,9,10,10,8,9,8,6,6,10,9,7,9,9,.
抽取的学生对两部作品打分的统计表：
《热辣滚烫》得分情况扇形统计图:
根据以上信息,解答下列问题：
(1)填空：______；______；______.
(2)根据上述数据,你认为该校八年级学生对哪部作品评价更高？请说明理由.(写出一条即可)；
(3)若该校八年级1000名学生都对这两部作品进行打分,你认为这两部作品一共大约可得到多少个满分？
24．某中学举行春季长跑比赛活动,小明从起点学校西门出发,途经市博物馆后按原路返还,沿比赛路线跑回终点学校西门.设小明离开起点的路程s(千米)与跑步时间t(分钟)之间的函数关系如图所示,其中从起点到市博物馆的平均速度是0.3千米/分钟,用时35分钟根据图象提供的信息,解答下列问题：
(1)求图中a的值,并求出所在直线方程；
(2)组委会在距离起点2.1千米处设立一个拍摄点C,小明从第一次过点C到第二次经过点C所用的时间为68分钟
①求所在直线的函数解析式；
②该运动员跑完赛程用时多少分钟？
25．如图,在正方形中,E是边上一点(点E不与点C,D重合),连接.
【感知】如图①,过点A作交于点F.易证.(不需要证明).
【探究】如图②,取的中点M,过点M作交于点F,交于点G.
(1)求证：；
(2)连接,若,则的长为______.
【应用】如图③,取的中点M,连接,过点C作交于点G,连接,.若,则四边形的面积为______.
26．某文具店计划购进一批羽毛球拍,已知进价、售价等信息如表所示：
(1)第一次用11400元购进了A、B两款羽毛球拍共100套,求A、B两款各购进多少套？
(2)如果第二次购进羽毛球拍共100套,且购进A款的数量不超过B款数量的三分之一,那么文具店如何进货才能获利最大?最大利润是多少?
27．如图,在平面直角坐标系中,已知直线交x轴于点A,交y轴于点B.直线与直线相交于点M,交x轴于点C,交y轴于点D.
(1)直接写出点B和点D的坐标；
(2)若点P是直线在第四象限内的一个动点,设点P的横坐标是x,的面积是S,求S与x之间的函数关系；
(3)在(2)的条件下,当时,在平面直角坐标系内存在点E,使以点B,E,P,M为顶点的四边形是平行四边形,请直接写出点E的坐标.
参考答案
1．答案：D
解析：A、,不能合并,故本选项错误；
B、2,不能合并,故本选项错误；
C、,故本选项错误；
D.,故本选项正确.
故选：D.
2．答案：C
解析：A、,不能构成直角三角形,故选项错误；
B、,不能构成直角三角形,故选项错误；
C、,能构成直角三角形,故选项正确；
D、,不能构成直角三角形,故选项错误.
故选：C.
3．答案：C
解析：∵,,,
∴一次函数的图象经过一、二、四象限,
故选C.
4．答案：B
解析：∵甲的方差是0.25,乙的方差是0.21,
∴乙的方差<甲的方差,
∴乙的成绩比甲稳定.
故选：B.
5．答案：B
解析：A、函数的图象与x轴交点坐标是,故本选项错误；
B、函数的图象经过第一、二、三象限,所以不经过第四象限,故本选项正确；
C、函数的图象向上平移2个单位长度得到函数的图象,故本选项错误；
D、函数值随自变量的增大而增大,故本选项错误；
故选B
6．答案：B
解析：如图,连接,交于点O,
四边形是矩形,
,,,
∵,
∴,
∴,
∴
∴
∵
∴
故选：B.
7．答案：B
解析：分四种情况：①当,时,和的图象均经过第一、二、三象限,不存在此选项；
②当,时,的图象经过第一、三、四象限,的图象经过第一、二、四象限,选项B符合此条件；
③当,时,的图象经过第一、二、四象限,的图象经过第一、三、四象限,不存在此选项；
④当,时,和的图象均经过第二、三、四象限,不存在此选项.
故选B.
8．答案：B
解析：由一次函数的性质可知,函数随x的增大而增大,函数随x的增大而减小,当时直线在直线的上方,
∴关于x的不等式的解集是.
故选：B.
9．答案：C
解析：如图,连接PB
∵四边形ABCD是菱形,其周长为12cm
∴,
∵,,
∴
即
故选：C.
10．答案：A
解析：连接,
∵将正方形边沿折叠到,
∴,,,,
在和中,
,
∴,
∴,,
∴,即,
∴,即,故①正确,
∵,,
∴,
设,则,,
∴在中,,
即,
解得：,
∴,
∴,
∴,,
∴不是等边三角形,
∴,故②错误,
∵,
∴,,
∴,即,
∵,,
∴垂直平分,
∴,故③正确,
∵,,
∴,故④正确,
综上所述,正确的选项是①③④,
故选：A.
11．答案：a
解析：∵
∴
故答案为：a.
12．答案：(或)(答案不唯一,正确即可)
解析：若使变为矩形,可添加的条件是：
；(对角线相等的平行四边形是矩形)
等.(有一个角是直角的平行四边形是矩形)
故答案为：或.
13．答案：6
解析：由折叠可得：,,,∴中,
.
设,则,.
∵中,,∴,解得：,∴.
∵ABCD是矩形,∴.
故答案为6.
14．答案：96.
解析：如图,
设菱形ABCD的边长为x,则,,,依题意有
,
解得,
,
则菱形ABCD的面积为.
故答案为96.
15．答案：
解析：解:∵函数是关于x的正比例函数,
∴且,
解得,或(不符合题意,舍去).
故答案为：.
16．答案：
解析：由“上加下减”的原则可知,将函数的图象向上平移6个单位长度所得函数的解析式为,
∵此时与x轴相交,则,
∴,即,
∴点坐标为.
故答案为：.
17．答案：②
解析：①由题意得,,所以四边形是平行四边形,其依据是两组对边分别平行的四边形是平行四边形,故①正确；
②因为两组对边的长度相等,所以四边形是平行四边形,又因为对角线相等,所以此平行四边形是矩形,所以其依据是对角线相等的平行四边形是矩形,故②错误；
③因为四边形是用两张等宽的纸条交叉重叠地放在一起而组成的图形,所以,,所以四边形是平行四边形(两组对边相互平行的四边形是平行四边形),
如图所示,过点D分别作,边上的高为,,则(两纸条相同,纸条宽度相同),
平行四边形的面积,
,
平行四边形为菱形(一组邻边相等的平行四边形是菱形),
故③正确；
④根据折叠原理,对折后可得：所得的四边形有三个直角,且一组邻边相等,所以可以裁出正方形纸片,故正确.
故答案为：②.
18．答案：
解析：如图所示,连接,
∵M,N分别是,的中点,
∴是的中位线,
∴,
∵四边形是正方形,
∴,
∴,
∴当最大时,最大,此时最大,
∵点E是上的动点,
∴当点E和点C重合时,最大,即的长度,
∴此时,
∴,
∴的最大值为.
故答案为：.
19．答案：或
解析：设AC和BE相交于点O.
当P在OA上时,
∵,,
∴是等边三角形,
∴,.
则.
在直角中,.
则；
当P在OC上时,.
故答案是：或.
20．答案：
解析：四边形是矩形,
,,,,
,
,
,
,
,
,
平行四边形的面积为,
故答案为：.
21．答案：(1)
(2)
解析：(1)原式
；
(2)原式
.
22．答案：(1)
(2)或6
解析：(1)设直线的解析式为：,
把,代入,
得,
解得,
∴直线解析式为：；
∵坐标为的点在直线上,
把代入,
得,
∴；
(2)∵,
∴当,,即,
∴当,,即
∴,,
∴,
∵在y轴上有一点P,
∴,,
则或者,
,
或,
∴或6.
23．答案：(1)10；8.5；8
(2)《飞驰人生2》,理由：《飞驰人生2》调查得分的平均数、中位数、众数均比《热辣滚烫》高
(3)300个满分
解析：(1)《热辣滚烫》调查得分为“10分”所占的百分比为：
,即;
《热辣滚烫》调查得分为“8分”的人数最多,因此众数是8,即；
《飞驰人生2》调查得分从小到大排列处在中间位置的两个数的平均数为,因此中位数是8.5,即；
故答案为：10；8.5；8；
(2)《飞驰人生2》,
理由：《飞驰人生2》调查得分的平均数、中位数、众数均比《热辣滚烫》高；
(3)(个),
答：这两部作品一共可得到300个满分.
24．答案：(1)
(2)①
②85分钟
解析：(1)∵从起点到市博物馆的平均速度是0.3千米/分钟,用时35分钟,
∴千米.
∴,
设直线的解析式为：,
把代入,得
,
解得,,
∴直线的解析式为：；
(2)①∵直线解析式为,
∴当时,,解得,
∵小明从第一次经过C点到第二次经过C点所用的时间为68分钟,
∴小明从起点到第二次经过C点所用的时间是,分钟,
∴直线经过,,
设直线解析式,
∴,,
解得,,
∴直线解析式为.
②小明跑完赛程用的时间即为直线与x轴交点的横坐标,
∴当时,,解得,
∴小明跑完赛程用时85分钟.
25．答案：探究：(1)证明见解析
(2)2
应用：9
解析：感知：四边形是正方形,
,,
,
,
,
,
在和中,
,
；
探究：(1)如图②,
过点G作于P,
四边形是正方形,
,,
四边形是矩形,
,
,
同感知的方法得,,
在和中,
,
,
,
(2)由(1)知,,
,点M是的中点,
,
；
应用：同探究(2)得,,
,
同探究(1)得,,
,
.
26．答案：(1)A款购进40套,B款购进60套
(2)A款购进25套,B款购进75套,获利最大,最大利润为2125元
解析：(1)设A款购进x套,则B款购进套,
依题意得,,
解得,,
∴(套),
∴A款购进40套,B款购进60套；
(2)设A款购进a套,则B款购进套,利润为w元,
依题意得,,
由题意知,,
解得,,
∵,
∴当时,w最大,最大值为2125元
∴A款购进25套,B款购进75套,获利最大,最大利润为2125元.
27．答案：(1),
(2)
(3)点E的坐标为或或
解析：(1)点B是直线与y轴的交点坐标,
,
点D是直线与y轴的交点坐标,
；
(2)如图1,直线与相交于M,
,
,,
,
点P是直线在第四象限内的一个动点,
,
,
(3)如图2,
由(2)知,,
当时,,
,
,
①当是对角线时,取的中点G,连接并延长取一点使,
设,
,,
的中点坐标为,
,
,,
,,
,
②当为对角线时,同①的方法得,；
③当为对角线时,同①的方法得,；
即：满足条件的点E的坐标为或或.
喜剧片
平均数
中位数
众数
《飞驰人生2》
8.2
b
9
《热辣滚烫》
7.8
8
c
进价(元/套)
售价(元/套)
A款：李宁610
135
160
B款：中国匹克
100
120