



- 第32练 空间点、直线、平面间的位置关系(精练:基础+重难点)-【一轮复习讲义】高考数学高频考点题型归纳与方法总结(新高考通用) 试卷 3 次下载
- 第33讲 空间直线、平面的平行(精讲)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用) 试卷 3 次下载
- 第34讲 空间直线、平面的垂直(精讲)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用) 试卷 3 次下载
- 第34练 空间直线、平面的垂直(精练:基础+重难点)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用) 试卷 3 次下载
- 第35讲 空间向量的运算及其坐标表示(精讲)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用) 试卷 3 次下载
第33练 空间直线、平面的平行(精练:基础+重难点)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用)
展开刷真题 明导向
一、解答题
1.(2023·全国·统考高考真题)如图,在三棱锥中,,,,,的中点分别为,点在上,.
(1)求证://平面;
【答案】(1)证明见解析
【分析】(1)根据给定条件,证明四边形为平行四边形,再利用线面平行的判定推理作答.
【详解】(1)连接,设,则,,,
则,
解得,则为的中点,由分别为的中点,
于是,即,
则四边形为平行四边形,
,又平面平面,
所以平面.
2.(2023·全国·统考高考真题)如图,在三棱锥中,,,,,BP,AP,BC的中点分别为D,E,O,,点F在AC上,.
(1)证明:平面;
【答案】(1)证明见解析;
【分析】(1)根据给定条件,证明四边形为平行四边形,再利用线面平行的判定推理作答.
【详解】(1)连接,设,则,,,
则,
解得,则为的中点,由分别为的中点,
于是,即,则四边形为平行四边形,
,又平面平面,
所以平面.
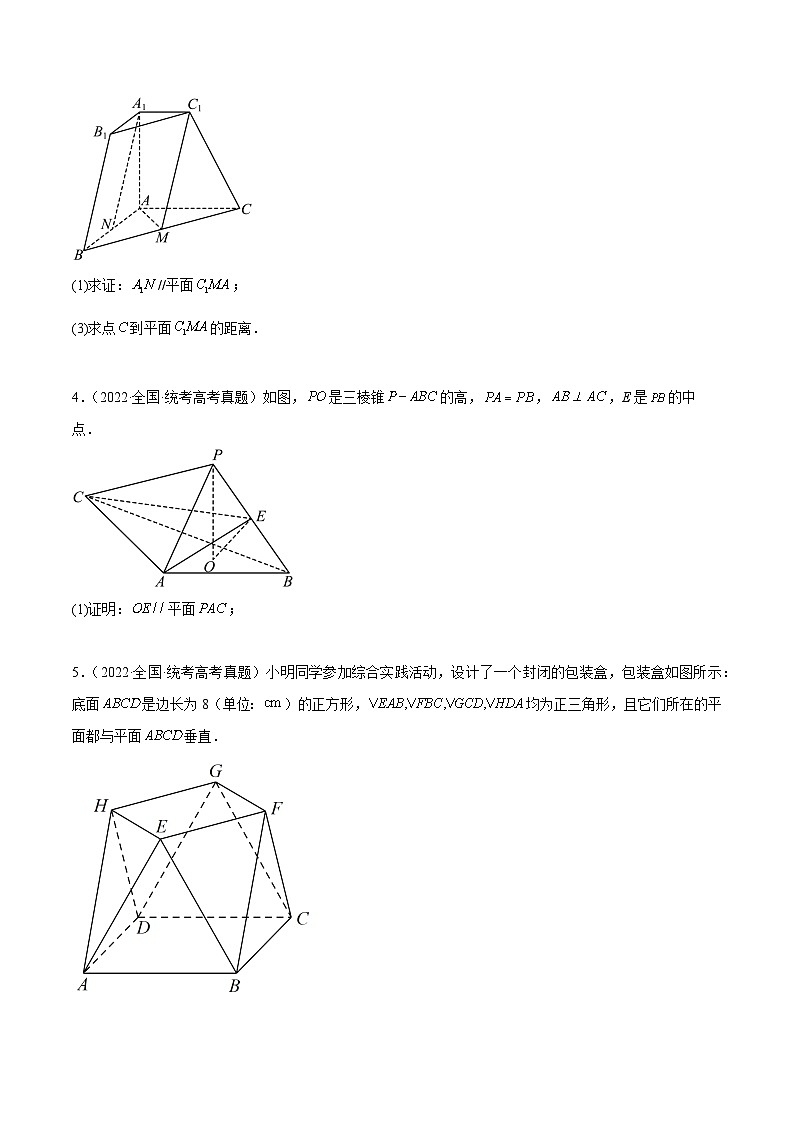
3.(2023·天津·统考高考真题)三棱台中,若面,分别是中点.
(1)求证://平面;
【答案】(1)证明见解析
【分析】(1)先证明四边形是平行四边形,然后用线面平行的判定解决;
【详解】(1)
连接.由分别是的中点,根据中位线性质,//,且,
由棱台性质,//,于是//,由可知,四边形是平行四边形,则//,
又平面,平面,于是//平面.
4.(2022·全国·统考高考真题)如图,是三棱锥的高,,,E是的中点.
(1)证明:平面;
【答案】(1)证明见解析
【分析】(1)连接并延长交于点,连接、,根据三角形全等得到,再根据直角三角形的性质得到,即可得到为的中点从而得到,即可得证;
【详解】(1)证明:连接并延长交于点,连接、,
因为是三棱锥的高,所以平面,平面,
所以、,
又,所以,即,所以,
又,即,所以,,
所以
所以,即,所以为的中点,又为的中点,所以,
又平面,平面,
所以平面
5.(2022·全国·统考高考真题)小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面是边长为8(单位:)的正方形,均为正三角形,且它们所在的平面都与平面垂直.
(1)证明:平面;
(2)求该包装盒的容积(不计包装盒材料的厚度).
【答案】(1)证明见解析;
(2).
【分析】(1)分别取的中点,连接,由平面知识可知,,依题从而可证平面,平面,根据线面垂直的性质定理可知,即可知四边形为平行四边形,于是,最后根据线面平行的判定定理即可证出;
(2)再分别取中点,由(1)知,该几何体的体积等于长方体的体积加上四棱锥体积的倍,即可解出.
【详解】(1)如图所示:
分别取的中点,连接,因为为全等的正三角形,所以,,又平面平面,平面平面,平面,所以平面,同理可得平面,根据线面垂直的性质定理可知,而,所以四边形为平行四边形,所以,又平面,平面,所以平面.
(2)[方法一]:分割法一
如图所示:
分别取中点,由(1)知,且,同理有,,,,由平面知识可知,,,,所以该几何体的体积等于长方体的体积加上四棱锥体积的倍.
因为,,点到平面的距离即为点到直线的距离,,所以该几何体的体积
.
[方法二]:分割法二
如图所示:
连接AC,BD,交于O,连接OE,OF,OG,OH.则该几何体的体积等于四棱锥O-EFGH的体积加上三棱锥A-OEH的倍,再加上三棱锥E-OAB的四倍.容易求得,OE=OF=OG=OH=8,取EH的中点P,连接AP,OP.则EH垂直平面APO.由图可知,三角形APO,四棱锥O-EFGH与三棱锥E-OAB的高均为EM的长.所以该几何体的体积
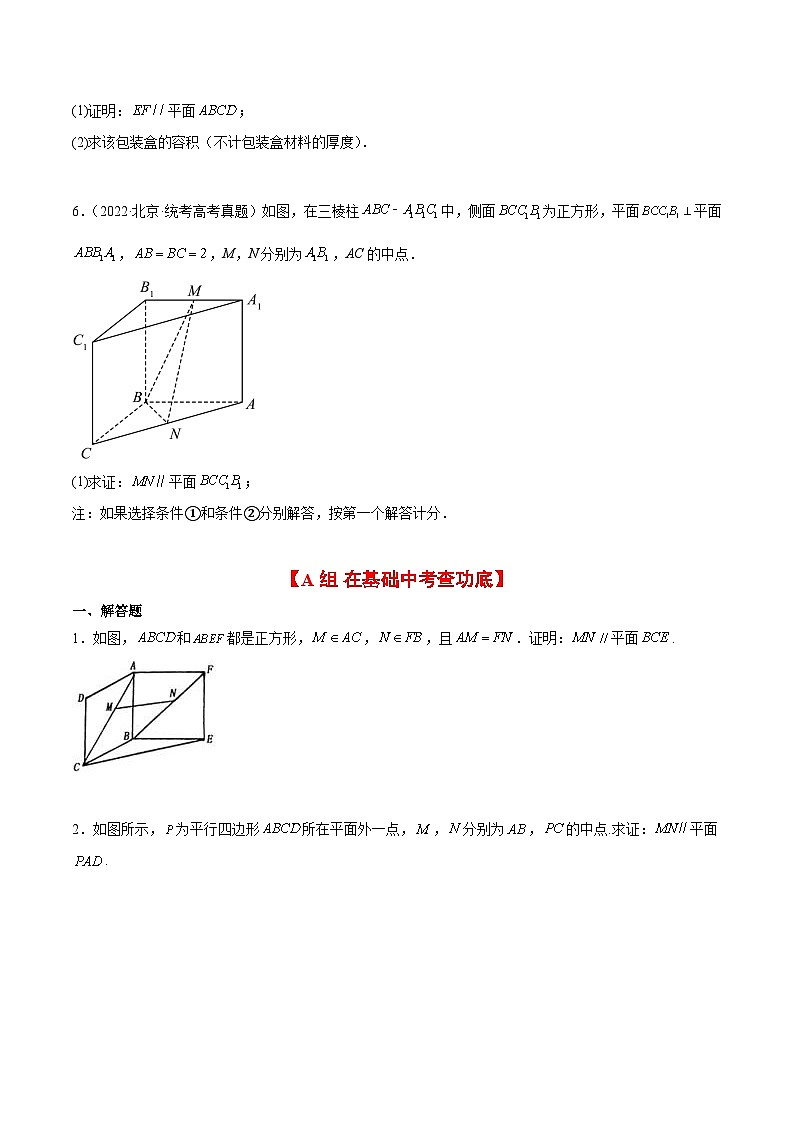
6.(2022·北京·统考高考真题)如图,在三棱柱中,侧面为正方形,平面平面,,M,N分别为,AC的中点.
(1)求证:平面;
【答案】(1)见解析
【分析】(1)取的中点为,连接,可证平面平面,从而可证平面.
【详解】(1)取的中点为,连接,
由三棱柱可得四边形为平行四边形,
而,则,
而平面,平面,故平面,
而,则,同理可得平面,
而平面,
故平面平面,而平面,故平面,
【A组 在基础中考查功底】
一、解答题
1.如图,和都是正方形,,,且.证明:平面.
【答案】见详解
【分析】由线面平行的判定定理即可证明结论.
【详解】
作交于,作交于.
连结,则,,
又,
故,
于是,且.
∴四边形为平行四边形,
故.
平面,平面,
∴平面
2.如图所示,为平行四边形所在平面外一点,,分别为,的中点.求证:平面.
【答案】证明见解析
【分析】取的中点,连接,,根据线面平行的判定定理,即可证明结论成立.
【详解】证明:取的中点,如图所示,连接,.
∵,分别为,的中点,∴,且.
∵四边形为平行四边形,为的中点,
∴且,∴平行且相等,
∴四边形为平行四边形,∴.
又平面,平面,
∴平面.
【点睛】本题主要考查证明线面平行,熟记线面平行的判定定理即可,属于常考题型.
3.如图所示,在三棱柱中,为的中点,求证:平面
【答案】证明见解析
【分析】连接交于,连接,则由平行四边形的性质和三角形中位线定理可得,然后利用线面平行的判定定理可证得结论
【详解】证明:如图,连接交于,连接,
∵四边形是平行四边形.∴点为的中点.
∵为的中点,∴为的中位线,∴.
∵平面,平面,∴平面.
4.已知四棱锥中,,取的中点M,的中点N,求证:平面.
【答案】证明见解析
【分析】如图,连接并延长,交的延长线于点E,连接,可得N为的中点,再由三角形中位线定理可得∥,然后由线面平行的判定定理可证得结论
【详解】证明:如图,连接并延长,交的延长线于点E,连接.
因为∥,N为的中点,
所以N为的中点.
因为M为的中点,
所以∥.
因为平面,平面,
所以∥平面.
5.如图,在长方体中,E为AB的中点,F为的中点.证明:平面.
【答案】证明见解析
【分析】取的中点G,连接GF,AG,证明四边形AEFG为平行四边形,进而有,然后根据线面平行的判断定理即可证明.
【详解】证明:取的中点G,连接GF,AG,
因为G为的中点,F为的中点,所以且CD=2GF,
又E为AB的中点,AB=CD,,所以且AE=GF,
所以四边形AEFG为平行四边形,所以,
因为平面,EF平面,
所以平面.
6.如图,几何体的底面ABCD为平行四边形,点M为PC中点,证明:平面BDM.
【答案】证明见解析
【分析】连接AC交BD于点O,连接OM,证明OM∥PA,即可证明PA∥平面BDM.
【详解】证明:连接AC交BD于点O,因为底面ABCD为平行四边形,所以O为AC中点,
在△PAC中,又M为PC中点,所以OM∥PA,
又PA⊄平面BDM,OM⊂平面BDM,
所以PA∥平面BDM.
7.如图所示,在正方体中,,,分别是,,的中点.求证:平面平面.
【答案】证明见解析
【分析】连接,由三角形中位线定理可得,再由正方形的性质可证得,则,利用线面平行的判定定理可证得平面,同理可证得平面,再利用面面平行的判定定理可证得结论.
【详解】证明:如图,连接.
因为,分别是,的中点,所以.
因为∥,,
所以四边形为平行四边形,
所以,
所以.
因为平面,平面,
所以平面.
同理可证平面.
又因为,,平面,
所以平面平面.
8.正三棱柱的底面正三角形的边长为,为的中点,.
(1)证明:平面;
(2)求该三棱柱的体积.
【答案】(1)证明见解析
(2)
【分析】(1)作出辅助线,由中位线得到线线平行,从而线面平行;
(2)求出底面正三角形的面积,进而利用柱体体积公式进行求解.
【详解】(1)证明:连接,设,连接
∵是正三棱柱的侧面,
∴为矩形,
∴是的中点,
∴是的中位线,
∴,
又平面,平面,
∴平面.
(2)因为在正三棱柱中,底面正三角形的边长为2,为的中点
所以,,
故,
又平面,,
所以正三棱柱的体积
9.如图,在正方体中,是的中点,分别是的中点,求证:
(1)平面;
(2)平面平面.
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)利用线面平行的判定定理即可证明;(2)利用面面平行的判定定理证明.
【详解】(1)
如图,连接,∵分别是的中点,∴.
又∵平面,平面,∴直线平面.
(2)连接SD,∵分别是 的中点,
∴.又∵平面,平面,
∴平面,由(1)知,平面,
且平面,平面,,∴平面∥平面.
10.如图,为圆锥的顶点,是圆锥底面的圆心,,为圆锥底面的两条直径,为母线上一点,连接,,.
(1)若为的中点,证明:平面;
(2)若平面,证明:为的中点.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)由中位线得,进而可得结论;
(2)由线面平行性质定理可得,由于为中点,进而可得结论.
【详解】(1)若为的中点,由为圆锥底面的直径,有为的中点.
则在中有,
又平面,平面,
则有平面;
(2)若平面,由平面,平面平面,
有,
所以在中,,
又为的中点,则有,
则有为的中点.
11.如图,在三棱柱中,,分别为线段,的中点.
(1)求证:平面.
(2)在线段上是否存在一点,使平面平面请说明理由.
【答案】(1)证明见解析
(2)存在,理由见解析
【分析】(1)根据中位线的性质可得A,再根据线面平行的判定可得B即可;
(2)取的中点,连接,根据中位线的性质判定即可
【详解】(1)证明:因为,分别为线段的中点所以A.因为,所以B.又因为平面,平面,所以平面.
(2)取的中点,连接,因为为的中点所以.
因为平面,平面,所以平面,
同理可得,平面,又因为,,平面,所以平面平面
故在线段上存在一点,使平面平面.
12.如图,在四棱柱ABCD﹣A1B1C1D1中,点M是线段B1D1上的一个动点,E,F分别是BC,CM的中点.
(1)求证:EF平面BDD1B1;
(2)设G为棱CD上的中点,求证:平面GEF平面BDD1B1.
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)根据线面平行的判定定理求证即可;
(2)根据面面平行的判定定理证明即可.
【详解】(1)证明:在四棱柱ABCD﹣A1B1C1D1中,连接BM,如图,
因E,F分别是BC,CM的中点,
则有EFBM,
又EF平面BDD1B1,BM平面BDD1B1,
所以EF平面BDD1B1.
(2)证明:取CD的中点G,连接EG,FG,如图,
而E是BC的中点,
于是得EGBD,
而EG平面BDD1B1,BD平面BDD1B1,
从而得EG平面BDD1B1,
由(1)知EF平面BDD1B1,
EFEG=E,且EF、EG平面GEF,
因此,平面GEF平面BDD1B1,所以当G是DC的中点时,平面GEF平面BDD1B1.
13.如图,四棱锥的底面是正方形,PA⊥平面ABCD,E,F分别为AB,PD的中点,且PA=AD=2.
(1)求证:平面PEC;
(2)求三棱锥的体积.
【答案】(1)证明见解析;
(2).
【分析】(1)取PC的中点G,由题可得,然后根据线面平行的判定定理即得;
(2)根据锥体的体积公式结合条件即得.
【详解】(1)取PC的中点G,连接EG,FG,
因为F是的中点,
所以,
因为E是AB的中点,
所以,
所以,
所以四边形是平行四边形,
所以,
因为平面,平面,
所以平面;
(2)因为PA⊥平面ABCD,F为PD的中点,且PA=AD=2,四边形ABCD是正方形,
所以三棱锥的体积为:
=
.
14.在四棱锥中,底面,四边形为边长为的菱形,,,为中点,为的中点.
(1)求证:直线平面;
(2)求直线与所成角大小.
【答案】(1)证明见解析
(2)
【分析】(1)作出辅助线,证明出平面平面PCD,从而得到线面平行;
(2)作出辅助线,由余弦定理得到,找到直线与所成的角或其补角为直线与所成角,由勾股定理求出,由余弦定理求出答案.
【详解】(1)取AD的中点E,连接NE,ME,
因为为中点,为的中点,
所以,,
因为平面PCD,平面PCD,
所以平面PCD,同理可得平面PCD,
因为,平面,
所以平面平面PCD,
因为平面MNE,
所以直线平面;
(2)连接AC,
四边形为边长为的菱形,,所以,
由余弦定理得:,
因为,为中点,所以,
因为底面,平面ABCD,
所以PA⊥AC,PA⊥AD,
所以,
,
因为,所以直线与所成的角或其补角为直线与所成的角,
由余弦定理得:,
故直线与所成角的大小为.
15.已知正方体,点E为中点,直线交平面于点F.求证:点F为中点.
【答案】证明见解析
【分析】先证明线面平行,然后利用线面平行的性质得到,结合E为中点可证结论.
【详解】在正方体中,所以;
因为平面,平面,
所以平面;
因为直线交平面于点F,
所以平面,且平面平面,
因为平面,平面,平面平面,
所以,
因为点E为中点,底面是正方形,
所以F为中点.
16.点是所在平面外一点,是中点,在上任取点,过和作平面交平面于.证明:.
【答案】证明见详解
【分析】连结,交于点,连结,可推得,进而得到平面.然后根据线面平行的性质定理可得.
【详解】证明:连结,交于点,连结.
因为四边形为平行四边形,所以是的中点.
又是中点,所以.
因为平面,平面,
所以平面.
又平面平面,平面,
所以.
17.已知直棱柱的底面ABCD为菱形,且,,点为的中点.
(1)证明:平面;
(2)求三棱锥的体积.
【答案】(1)证明见解析
(2)1
【分析】(1)根据平行四边形的判定定理和性质,结合菱形的性质、线面平行的判定定理进行证明即可;
(2)根据菱形的性质、直棱柱的性质,结合线面垂直的判定定理、三棱锥的体积公式进行求解即可.
【详解】(1)连接AC交BD于点,连接,
在直四棱柱中,,
所以四边形为平行四边形,即,,
又因为底面ABCD为菱形,所以点为AC的中点,
点为的中点,即点为的中点,所以,,
即四边形为平行四边形,所以,
因为平面,平面,,所以平面;
(2)在直棱柱中平面,平面,
所以,
又因为上底面为菱形,所以,
因为平面,
所以平面,
因为在中,,
且点为BD的中点,所以,即,
所以.
18.如图,在长方体中,,.
(1)设O、E分别为和AB中点,求证:OE平行于平面;
(2)求异面直线与所成角的大小.
【答案】(1)证明见解析
【分析】(1)首先取中点,连接、,易证四边形为平行四边形,所以,再利用线面平行的判定即可得到答案.
【详解】(1)取中点,连接、,如图所示:
因为O为中点,所以,且.
又是长方体,为中点,
所以,且,即,且,
四边形为平行四边形,所以.
又在平面内,在平面外,因此,平面.
19.如图,在正四面体中,,,,分别是,,的中点,取,的中点,,点为平面内一点
(1)求证:平面平面
(2)若平面,求线段的最小值,
【答案】(1)证明见解析
(2)
【分析】(1)先由线面平行判定定理证明线面平行,再由面面平行判定定理证明面面平行即可;
(2)由面面平行确定点在线段上,再求在边上的高,即的最小值.
【详解】(1)∵,分别为,的中点,∴,
又∵平面,平面,∴平面,
∵,分别为,的中点,∴,
又∵平面,平面,∴平面,
又∵,平面,平面,
∴平面平面.
(2)
由(1)知,平面平面,
∴若平面内存在一点,使平面,则在线段上,
∴线段的最小值为到直线的距离,即在边上的高,
∵,分别为,的中点,,分别为,的中点,
∴,
又∵,
∴,,
又∵,分别为,的中点,∴,同理,
∴当为中点时,,此时在边上的高,取最小值,
∴线段的最小值.
【B组 在综合中考查能力】
一、解答题
1.如图:在正方体中,M为的中点.
(1)求证:平面;
(2)在线段上是否存在一点N,使得平面平面,说明理由.
【答案】(1)证明见解析
(2)存在,理由见解析
【分析】(1)连接BD交AC于O,连接MO,通过证明可证明结论;
(2)上的中点N即满足平面平面,通过证明平面结合平面可证明结论.
【详解】(1)连接BD交AC于O,连接MO.
∵为正方体,底面为正方形,∴O为BD的中点.
∵M为的中点,在中,OM是的中位线,所以.
又平面,平面,∴平面;
(2)上的中点N即满足平面平面,
∵N为的中点,M为的中点,∴,且,
∴四边形为平行四边形,∴,
∵平面,平面,
∴平面;
由(1)知平面,
又∵,
∴平面平面.
2.如图所示,三棱柱,底面是边长为2的正三角形,侧棱底面,点分别是棱,上的点,点是线段的中点,.
(1)求证平面;
(2)求与所成角的余弦值.
【答案】(1)证明见解析;
(2)与所成角的余弦值为.
【分析】(1)取的中点,连接;证明,根据线面平行判定定理证明平面;
(2)根据异面直线夹角定义证明为直线与所成角,解三角形求其余弦值即可.
【详解】(1)取的中点,连接,
∵分别为的中点,∴,,
由,且,
∴,且 ,
∴四边形为平行四边形,故,
又平面,平面,
∴平面;
(2)因为,
所以为直线与所成角,
中,,
直角梯形中,,过作,为垂足,如图所示,
则,,,,
,所以为等腰三角形,则,
中,,
所以,
中,,
所以
所以与所成角的余弦值为.
3.如图,在正三棱柱中,是线段上靠近点的一个三等分点,是的中点.
(1)证明:平面;
(2)若,求点到平面的距离.
【答案】(1)证明见解析
(2)
【分析】(1)取线段的中点,连接,记,连接,证明,,从而可证得平面平面,再根据面面平行的性质即可得证;
(2)取棱的中点,以为原点,分别以,的方向为,轴的正方向,建立空间直角坐标系,利用向量法求解即可.
【详解】(1)取线段的中点,连接,记,连接,
因为,分别是,的中点,所以,
因为平面,平面,所以平面,
由题意可知四边形是矩形,则是的中点,
因为是的中点,所以,
因为平面,平面,所以平面,
因为平面,且,所以平面平面,
因为平面,所以平面;
(2)取棱的中点,以为原点,分别以,的方向为,轴的正方向,建立如图所示的空间直角坐标系,
因为,所以,,,,
则,,,
设平面的法向量为,
则,令,则,所以,
故点到平面的距离.
4.如图所示,在直三棱柱中,,,点、分别为棱、的中点,点是线段上的点(不包括两个端点).
(1)设平面与平面相交于直线,求证:;
【答案】(1)证明见解析
【分析】(1)证明出平面,,利用线面平行的性质可证得,利用平行线的传递型可证得结论成立;
【详解】(1)证明:因为点、分别为棱、的中点,则,
在三棱柱中,四边形为平行四边形,所以,,则,
因为平面,平面,所以,平面,
因为平面,平面平面,所以,,故.
5.在四面体中,四边形是矩形,且.
(1)证明:平面;
【答案】(1)证明见解析
【分析】(1)证明平面,即可证明,根据线面平行的判定定理即可证明结论;
【详解】(1)证明:因为四边形是矩形,故,
由于平面,平面,
故平面,又平面,平面平面,
故,又平面,平面,
故平面.
6.在四棱柱中,,,,.
(1)当时,试用表示;
(2)证明:四点共面;
(3)判断直线能否是平面和平面的交线,并说明理由.
【答案】(1)
(2)证明见解析
(3)答案见解析
【分析】(1)直接利用空间向量线性运算可得,再根据已知关系,,进行化简可得出结果.
(2)可设,不为),由题意可化简得到,将代入并结合题意可化简得出,即可证明出四点共面.
(3)先假设面面,根据棱柱的性质,可得出平面,进而得出,反之当,可判断出平面,平面,得出平面平面=,得出当时,直线是面和面的交线,反之不行,从而得出结果.
【详解】(1)=
==;
(2)设,不为),
=
则,,共面且有公共点,则四点共面;
(3)假设面面,在四棱柱中,
,面,面,则平面,
又面,面面,则;
反过来,当时,因为,则,
则确定平面
则平面,
又因为平面,
所以平面平面=,
所以是直线是面和面的交线的充要条件;
所以,当时,直线是面和面的交线;
当不平行时,直线不是面和面的交线
7.如图所示,三棱台的体积为7,其上、下底面均为等边三角形,平面平面,且,棱AC与BC的中点分别为G,H.
(1)证明:平面平面FGH;
(2)求点E到平面FGH的距离.
【答案】(1)证明见解析
(2)
【分析】(1)利用面面平行的判断定理,转化为证明线线平行;
(2)首先根据第一问转化为点到平面的距离,再根据等体积转化求点到平面的距离.
【详解】(1)证明:分别是的中点,
,
平面,平面,
平面,
又,,
∴四边形为平行四边形,∴.
平面,平面,
平面FGH,
平面ABED,平面ABED,,
∴平面平面FGH.
(2)平面ABED,由(1)知平面FGH,
点E到平面FGH的距离等于点A到平面FGH的距离,设为d.
由题意得上底面面积为,下底面面积为,
设三棱台的高为,则,得.
由,得,
设CG的中点为I,连接IH,IF,∵平面平面ABC且交于AC,,
∴平面ABC,,,
,
,
∵,∴,
故点E到平面FGH的距离为.
8.如图,在正三棱柱中,是的中点,求证:平面.
【答案】证明见解析
【分析】构建空间直角坐标系,设正三棱柱的底面边长为,侧棱长为,写出相关点坐标,求面的法向量、的坐标,判断、的位置关系,即可证结论.
【详解】如图,以为坐标原点建立空间直角坐标系,
设正三棱柱的底面边长为,侧棱长为,
则,,
所以.
设面法向量为,则,令,则.
由于,因此,平面,
所以.
9.如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,其中AD∥BC,AD=3,AB=BC=2,PA⊥平面ABCD,且PA=3.点M在棱PD上,点N为BC中点.
(1)证明:若DM=2MP,则直线MN∥平面PAB;
【答案】(1)证明见解析
【分析】(1)取,利用平行线分线段成比例和平行四边形的性质,结合线面平行的判定可证得MQ∥平面PAB,QN∥平面PAB,由面面平行的判定与性质可证得结论;
【详解】(1)在AD上取一点Q,使得,连接MQ,NQ,如图,
∵,∴MQ∥AP,又平面PAB,PA⊂平面PAB,
∴MQ∥平面PAB;
∵,,AD∥BC,
∴AQ∥BN,AQ=BN,∴四边形ABNQ为平行四边形,
∴AB∥QN,又平面PAB,AB⊂平面PAB,
∴QN∥平面PAB,又MQ∩QN=Q,MQ,QN⊂平面MNQ,
∴平面MNQ∥平面PAB,又MN⊂平面MNQ,
∴MN∥平面PAB;
10.如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,PA=PD,AB=AD,PA⊥PD,AD⊥CD,∠BAD=60°,M,N分别为AD,PA的中点.
(1)证明:平面BMN∥平面PCD;
【答案】(1)证明见解析
【分析】(1)平面BMN∥平面PCD证明的关键就是证明平面BMN 中的两条相交直线BM,MN平行于平面PCD,按此则结论可证.
【详解】(1)证明:连接BD,如图
∵AB=AD,∠BAD=60°,
∴△ABD为等边三角形,
∵M为AD的中点,
∴BM⊥AD,
∵AD⊥CD,
又CD,BM⊂平面ABCD,
BM∥CD,
又BM平面PCD,CD⊂平面PCD,
∴BM∥平面PCD,
∵M,N分别为AD,PA的中点,
∴MN∥PD,
又MN平面PCD,PD⊂平面PCD,
∴MN∥平面PCD.
又BM,MN⊂平面BMN,BM∩MN=M,
∴平面BMN∥平面PCD.
11.直四棱柱,,,,,
(1)求证:平面;
【答案】(1)证明见解析
【分析】(1)要证直线与平面平行,可以先证平面与平面平行,进而可证结论;
【详解】(1)因为是直四棱柱,所以,
又因为平面,平面,
平面,
因为,平面,平面,
所以平面,
又因为,平面,平面平面,
又平面,平面.
12.已知正方体,点为中点,直线交平面于点.
(1)证明:点为的中点;
【答案】(1)证明见解析.
【详解】(1)在正方体中,,又平面,且平面,
则平面,而交平面于点,即平面,
又平面,有平面,因此平面平面,
于是,而为中点,
所以为的中点.
13.在四棱锥中,平面,四边形为矩形,为棱的中点,与交于点为的重心.
(1)求证:平面;
【答案】(1)证明见解析
【分析】(1)利用相似证明线线平行,再利用线面平行判定定理证明线面平行;
【详解】(1)证明:延长交于点,连接,则为的中点,
因为为的中点,所以,
又,所以与相似,
所以,
因为为的重心,所以,
所以,所以与相似,
所以,
所以,
又平面,平面,
所以平面.
14.如图在棱长为的正方体中,是上一点,且平面.
(1)求证:为的中点;
【答案】(1)证明见解析
【分析】(1)连接交于点,连接,利用线面平行的性质可得出,推导出为的中点,结合中位线的性质可证得结论成立;
【详解】(1)证明:连接交于点,连接,
因为平面,平面,平面平面,
所以,,
因为四边形为正方形,,则为的中点,
因此,为的中点.
15.如图,在四棱锥中,底面是正方形,点E,F,N分别为侧棱PD,PC,PB的中点,M为PD(不包含端点)上的点,,.
(1)若,求证:平面;
【答案】(1)证明见解析
【分析】(1)延长FM和CD交于点Q,连BQ交AD于点H,连FH,FN,先证明H为AD的中点,再证明四边形为平行四边形,则,再根据线面平行的判定定理即可得证;
【详解】(1)延长FM和CD交于点Q,连BQ交AD于点H,连FH,FN,
由,故,
所以,
即H为AD的中点,
此时,,且,
所以四边形为平行四边形,故,
又平面,平面,
所以平面;
16.如图,多面体是将一个平行六面体截去三棱锥后剩下的几何体,P为三角形的重心,Q为的中点.四边形ABCD是边长为1的正方形,且,.
(1)求异面直线BC与所成角的大小;
【答案】(1)
【分析】(1)利用异面直线的定义作出异面直线所成的角,然后在三角形中求解即可;
【详解】(1)因为多面体是平行六面体截去三棱锥后剩下的几何体,
所以,所以为异面直线BC与所成角或其补角,
因为,Q为的中点,,所以,,
因为四边形ABCD是边长为1的正方形,所以为等边三角形,即,
所以异面直线BC与所成角的大小.
【C组 在创新中考查思维】
一、解答题
1.如图,在四棱锥中,PA面ABCD,ABCD,且CD=2,AB=1,BC=,PA=1,ABBC,N为PD的中点.
(1)求证:AN平面PBC;
【答案】(1)见解析
【分析】(1)取的中点,连接,证明,,从而可得平面平面,再根据面面平行的性质即可得证;
【详解】(1)证明:取的中点,连接,
因为N为PD的中点,
所以,
又平面,平面,
所以平面,
因为,
所以四边形为平行四边形,
所以,
又平面,平面,
又因平面,
所以平面平面,
又平面,
所以平面;
2.如图,在棱长为2的正方体中,点M是正方体的中心,将四棱锥绕直线逆时针旋转后,得到四棱锥.
(1)若,求证:平面平面;
【答案】(1)证明见解析
【分析】(1)根据面面平行的判定定理即可证明结论;
【详解】(1)证明:若,则平面、平面为同一个平面,
连接,则M是中点,是中点,
故是的中位线,所以.
因为,所以平面四边形是平行四边形,所以.
又平面平面,所以平面
同理平面,且平面平面,
所以,平面平面.
3.把底面为椭圆且母线与底面垂直的柱体称为“椭圆柱”.如图,椭圆柱中底面长轴,短轴长,为下底面椭圆的左右焦点,为上底面椭圆的右焦点,,P为的中点,MN为过点的下底面的一条动弦(不与AB重合).
(1)求证:平面PMN
(2)求三棱锥的体积的最大值.
【答案】(1)证明见解析;
(2)2
【分析】(1)由线线平行证线面平行;
(2)由解析法,建立平面直角坐标系如图所示,,转为求的最大值,
其中为弦长公式结合韦达定理求得,为到直线MN的距离由点线距离公式求得. 最后讨论最值即可.
【详解】(1)由长轴,短轴长得焦半径得,∴分别OB、的中点,
在柱体中,纵切面为矩形,连接,则,又,∴四边形为平行四边形,∴,
∵P为的中点,,∴,
∵平面PMN,平面PMN,∴平面PMN;
(2),
建立平面直角坐标系如图所示,则底面椭圆为,,
由题意知,直线MN的斜率不为0,设为,,联立椭圆方程可得,
则,∴.
又点到直线MN的距离.
∴.
∴.
设,对,由,∴在上单调递增,
∴,此时.
故三棱锥的体积的最大值为2.
【点睛】圆锥曲线三角形面积问题,一般由弦长公式结合韦达定理求得一边长,再由点线距离公式求得高,从而表示出面积,作进一步讨论.
4.如图,在多面体中,平面平面,平面,和均为正三角形,,.
(1)在线段上是否存在点F,使得平面?说明理由;
【答案】(1)存在,理由见解析
【分析】(1)记中点为M,连结,根据线面平行的判定定理即可得出结论;
【详解】(1)记中点为M,连结,为正三角形,,
则,且.
因为平面平面 ,平面平面,平面ACD,
所以平面,又因为平面,
所以.
延长交于点G,则为平面与平面的交线,
因为,故,所以B为的中点,
取中点F,连结,则,因为平面 ,平面,
所以平面.
即线段上存在点F,当时,平面.
5.如图,在四棱锥中,,,,分别为,的中点,点在上,且为三角形的重心.
(1)证明:平面;
【答案】(1)证明见解析
【分析】(1)连接,连接并延长交于点,连接,首先说明,由重心的性质得到,即可证明,从而得证;
【详解】(1)证明:连接,因为,,所以,且,
由,得,,
则,所以.
连接并延长交于点,如图,
因为为的重心,所以.
连接,因为,所以.
又平面,平面,故平面.
6.如图,点在以为直径的圆上不同于,,垂直于圆所在平面,为的重心,,在线段上,且.
(1)证明:∥平面;
【答案】(1)证明见解析
【分析】(1)连接,并延长交于点,连接,由重心的性质和平行线的判定,结合线面平行的判定定理可证得结论,
【详解】(1)证明:连接,并延长交于点,连接,
因为为的重心,所以,
因为,所以,
所以∥,
因为平面,平面,所以∥平面;
7.如图,在三棱柱中,底面是边长为2的正三角形,,平行于和的平面分别与交于四点.
(1)试判断四边形的形状,并说明理由;
【答案】(1)四边形是矩形,理由见解析
【分析】(1)首先根据面面平行的判定以及面面平行的性质证明线线平行,然后证明四边形是矩形;
【详解】(1)四边形是矩形,下面给出证明:
因为,由题意//平面//平面,
面,
所以平面//平面,又平面平面,平面平面,
所以,同理,又,
所以,同理,
所以四边形是平行四边形.
取中点,连接,则.
又因为,所以,故有.
AP、A1P交于P且都在面AA1P内,所以平面又面
所以,
综上知:,即四边形是矩形.
8.已知三棱锥中,平面,,,为中点,为中点,在上,.二面角的平面角大小为.
(1)求证:平面;
【答案】(1)证明见解析
【分析】(1)连接并延长,交于点,取的中点可得,根据为中点,可得,从而,再由线面平行的判定定理可得答案;
【详解】(1)连接并延长,交于点,取的中点,连接,
因为为中点,所以,,所以,
所以,又为中点,所以,
所以,因为,所以,
所以,可得,
因为平面,平面,所以平面;
9.如图,在矩形中,点在边上,且满足,将沿向上翻折,使点到点的位置,构成四棱锥.
(1)若点在线段上,且平面,试确定点的位置;
【答案】(1)点为线段上靠近点的三等分点
【分析】(1)在取点使,根据线面平行的判定定理、面面平行的判定及性质定理即得;
【详解】(1)点为线段上靠近点的三等分点,
证明如下:
如图,
在取点,连接,,使得,
又,所以四边形为平行四边形,所以,
又平面平面,所以平面.
又平面,,平面,
所以平面平面,
又平面平面,平面平面,
所以,所以在中,,所以,
所以点为线段上靠近点的三等分点.
10.如图,在四棱锥中,平面,平面,底面为矩形,点在棱上,且与位于平面的两侧.
(1)证明:平面;
【答案】(1)证明见解析
【分析】(1)根据线面垂直的性质定理可得,根据线面平行的判定定理即可得平面,根据及线面平行的判定定理即可得平面,根据及面面平行的判定定理即可得平面平面,再根据面面平行的性质定理即可证明;
【详解】(1)证明:因为平面,
平面,
所以,
因为平面,平面,
所以平面,
因为底面为矩形,
所以,
因为平面,平面,
所以平面,
因为,
且平面,平面,
所以平面平面,
又因为平面,
所以平面;
第01练 集合(精练:基础+重难点)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用): 这是一份第01练 集合(精练:基础+重难点)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用),文件包含分层作业01集合精练基础+重难点原卷版docx、分层作业01集合精练基础+重难点解析版docx等2份试卷配套教学资源,其中试卷共31页, 欢迎下载使用。
第42练 直线与椭圆(精练:基础+重难点)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用): 这是一份第42练 直线与椭圆(精练:基础+重难点)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用),文件包含第42练直线与椭圆精练基础+重难点原卷版docx、第42练直线与椭圆精练基础+重难点解析版docx等2份试卷配套教学资源,其中试卷共165页, 欢迎下载使用。
第34练 空间直线、平面的垂直(精练:基础+重难点)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用): 这是一份第34练 空间直线、平面的垂直(精练:基础+重难点)-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结(新高考通用),文件包含第34练空间直线平面的垂直精练基础+重难点原卷版docx、第34练空间直线平面的垂直精练基础+重难点解析版docx等2份试卷配套教学资源,其中试卷共130页, 欢迎下载使用。













