2023-2024学年福建省福州市格致中学高二（下）期末数学试卷（含解析）

展开

这是一份2023-2024学年福建省福州市格致中学高二（下）期末数学试卷（含解析），共17页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

1.P为抛物线y2=2px(p>0)上一点，点P到抛物线准线和对称轴的距离分别为10和6，则p=( )
A. 2B. 4C. 4或9D. 2或18
2.已知p：0A. 03.已知集合A={(x,y)|y=x+1，0≤x≤1}，集合B={(x,y)|y=2x，0≤x≤10}，则集合A∩B=( )
A. {1,2}B. {x|0≤x≤1}C. {(1,2)}D. ⌀
4.在边长为2的菱形ABCD中，∠BAD=60°,AE=xAB+1−x3AD,x∈[0,1]，则DE⋅DC的最小值为( )
A. −2B. −43C. −23D. −12
5.若实数a，b满足a>0，b>0，则“a>b”是“a+lna>b+lnb”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充分必要条件D. 既不充分也不必要条件
6.(2x2−5x)(2+1 x)7的展开式中含x项的系数为( )
A. 1984B. 960C. 660D. 704
7.已知sinα=2 67，cs(α−β)= 105，且0<α<3π4，0<β<3π4，则sinβ=( )
A. 9 1535B. 11 1035C. 1535D. 1035
8.如图，在棱长为2的正方体ABCD−A1B1C1D1中，E、F、G、M、N均为所在棱的中点，动点P在正方体表面运动，则下列结论中正确的个数为( )
①当点P为BC中点时，平面PEF⊥平面GMN
②异面直线EF、GN所成角的余弦值为14
③点E、F、G、M、N在同一个球面上
④若A1P=tA1A+A1M−2tA1B1，则P点轨迹长度为 52
A. 0B. 1C. 2D. 3
二、多选题：本题共4小题，共20分。在每小题给出的选项中，有多项符合题目要求。
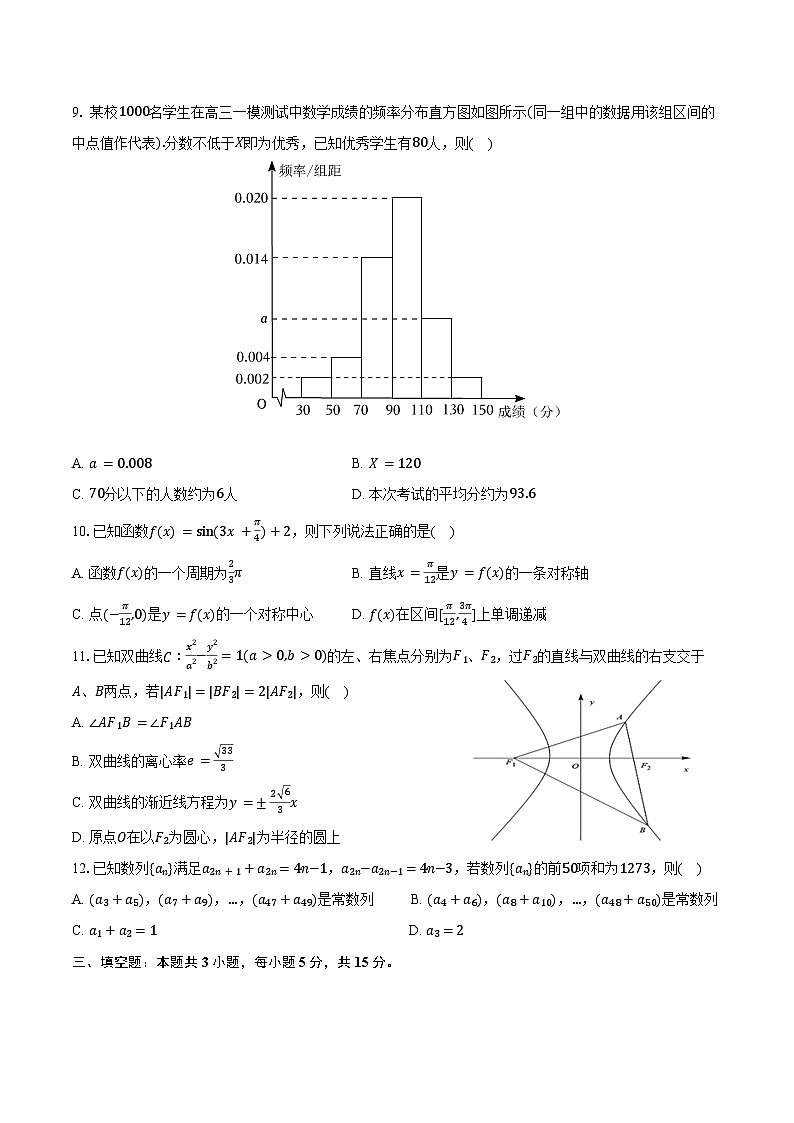
9. 某校1000名学生在高三一模测试中数学成绩的频率分布直方图如图所示(同一组中的数据用该组区间的中点值作代表).分数不低于X即为优秀，已知优秀学生有80人，则( )
A. a=0.008B. X=120
C. 70分以下的人数约为6人D. 本次考试的平均分约为93.6
10.已知函数f(x)=sin(3x+π4)+2，则下列说法正确的是( )
A. 函数f(x)的一个周期为23πB. 直线x=π12是y=f(x)的一条对称轴
C. 点(−π12,0)是y=f(x)的一个对称中心D. f(x)在区间[π12,3π4]上单调递减
11.已知双曲线C：x2a2−y2b2=1(a>0,b>0)的左、右焦点分别为F1、F2，过F2的直线与双曲线的右支交于A、B两点，若|AF1|=|BF2|=2|AF2|，则( )
A. ∠AF1B=∠F1AB
B. 双曲线的离心率e= 333
C. 双曲线的渐近线方程为y=±2 63x
D. 原点O在以F2为圆心，|AF2|为半径的圆上
12.已知数列{an}满足a2n+1+a2n=4n−1，a2n−a2n−1=4n−3，若数列{an}的前50项和为1273，则( )
A. (a3+a5)，(a7+a9)，…，(a47+a49)是常数列 B. (a4+a6)，(a8+a10)，…，(a48+a50)是常数列
C. a1+a2=1 D. a3=2
三、填空题：本题共3小题，每小题5分，共15分。
13.已知曲线f(x)=x3+x−3x13在x=1处的切线与g(x)=acsx在x=π2处的切线平行，则a的值为______．
14.已知tanα=12，且α∈(π,3π2)，则cs(α−π2)=______．
15.如图，在△ABC中，AD=12AB，AE=13AC，CD与BE交于点P，AB=2，AC=4，AP⋅BC=2，则AB⋅AC的值为______．
四、解答题：本题共6小题，共72分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题12分)
如图1，在平面四边形PBCD中，已知BC⊥PB，PD⊥CD，PB=6，BC=2，DP=2CD，DA⊥PB于点A.将△PAD沿AD折起使得PA⊥平面ABCD，如图2，设MD=λPD(0≤λ≤1)．

(1)若λ=23，求证：PB//平面MAC；
(2)若直线AM与平面PCD所成角的正弦值为 63，求λ的值．
17.(本小题12分)
已知三棱柱ABC−A1B1C1中，∠ACB=90°，BB1=2BC，AA1⊥平面ABC，AC=BC，E为AB的中点，D为A1B1上一点．
(1)求证：AD⊥CE；
(2)当D为A1B1的中点时，求二面角C−AD−B1的余弦值．
18.(本小题12分)
在△ABC中，a，b，c分别是角A、B、C的对边，m=(2b−c,csC)，n=(a,csA)，且m//n．
(1)求角A的大小；
(2)求y=2sin2B+cs(π3−2B)的值域．
19.(本小题12分)
如图所示，多面体ABCDEF中，AD//EF//BC，平面ADEF⊥平面BCEF，AD⊥EC，且AD=CD=2，CB=EF=1，∠BCD=π3．
(1)证明：BF⊥DE；
(2)若FB= 2，求直线DC与平面ABF所成角的正弦值．
20.(本小题12分)
某网店经营的一种商品进价是每件10元，根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示，该网店与这种商品有关的周开支均为25元．
(Ⅰ)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式；
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式；当该商品的销售价格为多少元时，周利润最大？并求出最大周利润．
21.(本小题12分)
已知函数f(x)=eax⋅csx，其中a∈R．
(1)若a=2，求曲线y=f(x)在点(0,f(0))处的切线方程；
(2)已知f(x)在区间(0,π)上存在唯一的极小值点．
(ⅰ)求实数a的取值范围；
(ⅱ)记f(x)在区间(0,π)上的极小值为g(a)，讨论函数g(a)的单调性．
答案解析
1.D
【解析】解：由抛物线y2=2px(p>0)可得准线l的方程为：x=−p2，
设点P(x1,y1)，∴y12=2px1，
∵点P到准线及对称轴的距离分别为10和6，
∴x1+p2=10，|y1|=6，y12=2px1，
解得x1=1，p=18，或x1=9，p=2，
即p为2或18．
故选：D．
2.A
【解析】解：因为p：0所以只有A选项是p的一个必要不充分条件．
故选：A．
3.C
【解析】解：集合A={(x,y)|y=x+1，0≤x≤1}，
集合B={(x,y)|y=2x，0≤x≤10}，
由y=x+1y=2x，解得x=1y=2，其中0≤x≤1；
∴集合A∩B={(1,2)}．
故选：C．
4.B
【解析】解：已知在边长为2的菱形ABCD中，∠BAD=60°,AE=xAB+1−x3AD,x∈[0,1]，
则AB⋅AD=2×2×12=2，
则DE⋅DC=(AE−AD)⋅AB=AE⋅AB−AD⋅AB=xAB2−2+x3AB⋅AD=10x−43，
又x∈[0,1]，
则当x=0时，DE⋅DC取最小值−43．
故选：B．
5.C
【解析】解：设f(x)=x+lnx，显然f(x)在(0,+∞)上单调递增，
∵a>b，
∴f(a)>f(b)，
∴a+lna>b+lnb，
故充分性成立，
∵a+lna>b+lnb”，
∴f(a)>f(b)，
∴a>b，
故必要性成立，
故“a>b”是“a+lna>b+lnb”的充要条件，
故选：C．
6.D
【解析】解：因为(2+1 x)7的展开式的通项为Tr+1=C7r⋅27−r⋅x−r2，r=0，1，2，…，7．
所以(2x2−5x)⋅(2+1 x)7的展开式中含x项的系数为2×C72×25+(−5)×C70×27=1344−640=704．
故选：D．
7.A
【解析】解：由sinα=2 67，0<α<3π4，可得0<α<π2，csα= 1−sin2α= 1−2449=57，
由0<α<π2，0<β<3π4，可得−3π4<α−β<π2，可得sin(α−β)=± 1−cs2(α−β)=± 1−1025=± 155，
则sinβ=sin[α−(α−β)]=sinαcs(α−β)−csαsin(α−β)=2 67× 105−57× 155=− 1535
或=2 67× 105−57×(− 155)=9 1535，
由于0<β<3π4，可得sinβ>0，则sinβ=9 1535，
故选：A．
8.D
【解析】解：结论①，取AD中点Q，连接PQ，FQ，在棱长为2的正方体ABCD−A1B1C1D1中，
E、F、G、M、N均为所在棱的中点，
易知GM⊥PQ，∵FQ//DD1，∴FQ⊥平面ABCD，
又GM在面ABCD内，∴GM⊥FQ，
∵FQ，PQ⊂平面PQF，PQ∩FQ=Q，
∴GM⊥平面PQF，又PF⊂面PQF，∴GM⊥PF，
连接BA1，ABB1A1是正方形，GN⊥A1B，
∵FA1⊥平面ABA1B1，GN⊂平面ABA1B1，∴GN⊥A1F，
FA1⊂平面PFA1B，A1B⊂平面PFA1B，A1B∩FA1=A1，
∴GN⊥平面PFA1B，PF⊂平面PFA1B，∴GN⊥PF，
综上，GN，GM⊂平面GMN，又GM∩GN=G，
所以PF⊥平面GMN，又PF⊂平面PEF，
故平面PEF⊥平面GMN，故①正确；
结论②，取A1B1中点T，连接ET，FT，则ET//GN，
∴∠TEF是异面直线EF，GN所成的角，
又EF=FT=ET= 2，则∠TEF=π3,cs∠TEF=12，故②错误；
结论③，记正方体的中心为点O，则|OE|=|OF|=|OG|=|OM|=|ON|= 2，
故点E，F，G，M，N在以O为球心，以 2为半径的球面上，故③正确；
结论④，∵A1P=tA1A+A1M−2tA1B1，E是A1A的中点，
∴A1P−A1M=2tA1E−2tA1B1，故MP=2tB1E，
∴P点轨迹是过点M与B1E平行的线段MP′，且|CP′|=12，
∴|MP′|= 52，故④正确；
综上，正确结论有①③④，共3个．
故选：D．
9.AD
【解析】解：对于A，(0.002×2+0.004+a+0.014+0.02)×20=1⇒a=0.008，A正确；
对于B，因为第六组有40人，第五组有160人，
所以130−X130−110=40160⇒X=125，B错误；
对于C，70分以下的人数为(0.002+0.004)×20×1000=120人，C错误；
对于D，平均成绩X−=40×0.04+60×0.08+80×0.28+100×0.4+120×0.16+140×0.04=93.6，D正确，
故选：AD．
10.AB
【解析】解：对于选项A，ω=3，所以最小正周期T=2π3，故选项A正确；
对于选项B，将x=π12代入函数解析式得：f(π12)=sin(3×π12+π4)+2=sinπ2+2，
所以x=π12是一条对称轴，故选项B正确；
对于选项C，因为f(x)可以看作是函数y=sin(3x+π4)向上平移2个单位后的函数，所以对称中心的纵坐标不可能是0，故选项C错误；
对于选项D，当x∈[π12,3π4]时，3π4−π12=2π3，刚好是函数f(x)的一个周期，不可能是单调的函数，故选项D错误．
故选：AB．
11.ABC
【解析】解：如图，
设|AF1|=|BF2|=2|AF2|=2m，则|AB|=|AF2|+|BF2|=3m，
由双曲线的定义知，|AF1|−|AF2|=2m−m=2a，即m=2a；|BF1|−|BF2|=2a，即|BF1|−2m=2a，
∴|BF1|=3m=|AB|，∴∠AF1B=∠F1AB，故选项A正确；
由余弦定理知，在△ABF1中，cs∠AF1B=|AF1|2+|BF1|2−|AB|22⋅|AF1|⋅|BF1|=4m2+9m2−9m22⋅2m⋅3m=13，
在△AF1F2中，cs∠F1AB=|AF1|2+|AF2|2−|F1F2|22⋅|AF1|⋅|AF2|=4m2+m2−4c22⋅2m⋅m=cs∠AF1B=13，
化简整理得，12c2=11m2=44a2，
∴离心率e=ca= 4412= 333，故选项B正确；
双曲线的渐近线方程为y=±bax=± c2−a2a2x=± e2−1x=±2 63x，故选项C正确；
若原点O在以F2为圆心，AF2为半径的圆上，则c=m=2a，与ca= 333不符，故选项D错误．
故选：ABC．
12.ACD
【解析】解：由a2n+1+a2n=4n−1，a2n−a2n−1=4n−3，
得a2n−1+a2n+1=2，
则(a3+a5)，(a7+a9)，…，(a47+a49)是各项均为2的常数列，A正确；
由a2n−a2n−1=4n−3，得a2n+2−a2n+1=4n+1，
又a2n+1+a2n=4n−1，
所以a2n+a2n+2=8n，
则(a4+a6)，(a8+a10)，……(a48+a50)是以16为首项，16为公差的等差数列，B错误；
数列{an}的前50项和为a1+a2+⋯+a50
=(a1+a2)+(a3+a5)+(a7+a9)+⋯+(a47+a49)+(a4+a6)+(a8+a10)+⋯+(a48+a50)
=(a1+a2)+2×12+16×12+12×112×16=(a1+a2)+1272=1273，
所以a1+a2=1，C正确；
在a2n−a2n−1=4n−3中，
令n=1，得a2−a1=1，又a1+a2=1，
所以a1=0，a2=1，
在a2n+1+a2n=4n−1中，
令n=1，得a3+a2=3，
所以a3=2，D正确．
故选：ACD．
13.−3
【解析】解：f′(x)=3x2+1−x−23，g′(x)=−asinx
由题意可知，g′(π2)=f′(1)，即−asinπ2=3，解得a=−3．
故答案为：−3．
14.− 55
【解析】解：∵tanα=12=sinαcsα，且α∈(π,3π2)，
∴csα=2sinα，
又∵cs2α+sin2α=1，解得：(2sinα)2+sin2α=1，解得：sinα=− 55，
∴cs(α−π2)=cs(π2−α)=sinα=− 55．
故答案为：− 55．
15.2
【解析】解：令BP=mBE，CP=nCD，
则AP=AB+mBE=AB+m(−AB+13AC)=(1−m)AB+m3AC，
AP=AC+nCD=AC+n(−AC+12AB)=n2AB+(1−n)AC，
则1−m=n2m3=1−n，解得m=35n=45，
则AP=25AB+15AC
AP⋅BC=AP⋅(AC−AB)=(25AB+15AC)⋅(AC−AB)=2，即15AC2−25AB2+15AB⋅AC=2，
解得AB⋅AC=2．
故答案为：2．
16.解：(1)证明：在平面四边形PBCD中，∵BC⊥PB，PB=6，BC=2，
∴CP=2 10，tan∠BPC=13，又PD⊥CD，DP=2CD，
∴CD=2 2，PD=4 2，tan∠DPC=12，
∴tan∠BPD=tan(∠BPC+∠DPC)=12+131−12×13=1，∴∠BPD=45°．
∴在Rt△PAD中，易得PA=AD=4．
∵DA⊥PB，BC⊥PB，∴AD//BC．
在四棱锥P−ABCD中，连接BD，设BD∩AC=F，连接MF，

∵λ=23，∴DMMP=2，又ADBC=DFFB=2，
∴MF//PB，又MF⊂平面MAC，PB⊄平面MAC，
∴PB//平面MAC．
(2)由题意易知AB，AD，AP两两垂直，故建系如图：

则A(0,0,0)，C(2,2,0)，D(0,4,0)，P(0,0,4)，
∴CD=(−2,2,0)，PD=(0,4,−4)．
设平面PCD的法向量为n=(x,y,z)，
则n⋅CD=0n⋅PD=0，即−2x+2y=04y−4z=0，取n=(1,1,1)，
由MD=λPD，得MD=(0,4λ,−4λ)，
∴M(0,4−4λ,4λ)，AM=(0,4−4λ,4λ)．
由直线AM与平面PCD所成角的正弦值为 63，
得|cs〈AM,n〉|=|AM⋅n|AM||n||=|4−4λ+4λ| (4−4λ)2+(4λ)2⋅ 3= 63，解得λ=12．
【解析】(1)利用线面平行的判定定理即可证明；
(2)利用空间向量的坐标表示，表示出线面夹角的余弦值即可求解．
17.(1)证明：因为AC=BC，E为AB的中点，
所以CE⊥AB.因为AA1⊥平面ABC，CE⊂平面ABC，
所以AA1⊥CE.因为AA1∩AB=A，
所以CE⊥平面ABB1A1．
因为AD⊂平面ABB1A1，所以AD⊥CE．

(2)解：以C点为坐标原点，CA，CB，CC1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系．
不妨设AC=BC=1，则A(1,0,0)，C(0,0,0)，D(12,12,2)，E(12,12,0)．
所以CA=(1,0,0)，CD=(12,12,2)．
易知平面ABB1A1的一个法向量为CE=(12,12,0)．
设平面ACD的法向量为m=(x,y,z)，
则m⋅CA=0,m⋅CD=0,即x=0,12x+12y+2z=0,亦即x=0,y+4z=0.
令z=−1，则平面ACD的一个法向量为m=(0,4,−1)．
所以|cs〈m,CE〉|=|CE⋅m||CE||m|=2 24× 17=2 3417．
故二面角C−AD−B1的余弦值为2 3417．
【解析】(1)证明CE⊥AB.AA1⊥CE.推出CE⊥平面ABB1A1.即可证明AD⊥CE．
(2)以C点为坐标原点，CA，CB，CC1所在直线分别为x轴、y轴、z轴建立空间直角坐标系．求出平面ABB1A1的一个法向量，平面ACD的法向量，利用空间向量的数量积求解二面角C−AD−B1的余弦值即可．
18.解：(1)由m//n得(2b−c)⋅csA−acsC=0，
由正弦定理得2sinBcsA−sinCcsA−sinAcsC=0，2sinBcsA−sin(A+C)=0，
∴2sinBcsA−sinB=0，
∵A,B∈(0,π)∴sinB≠0,csA=12，∴A=π3
(2)y=sin2B+csπ3cs2B+sinπ3sin2B，=1−12cs2B+ 32sin2B．
=sin(2B−π6)+1，
由(1)得0∴sin(2B−π6)∈(−12,1]∴y∈(12,2]．
答：角A的大小；函数的值域为y∈(12,2]
【解析】(1)用向量的共线的充要条件及三角形中的正弦定理求得角A．
(2)用三角函数的二倍角公式化简函数，再利用正弦函数的图象求出范围．
19.(1)证明：∵EF//BC且EF=BC，
∴四边形EFBC为平行四边形，
∴BF//EC，
又AD//EF，AD⊥EC，
∴BF⊥EF，
∵平面ADEF⊥平面BCEF，且平面ADEF∩平面BCEF=EF，BF⊂平面BCEF，
∴BF⊥平面ADEF，
又DE⊂平面ADEF，
∴BF⊥DE．

(2)解：连接DF，
在△BCD中，由余弦定理知，BD2=BC2+CD2−2BC⋅CDcs∠BCD=1+4−2×1×2×12=3，
∴CD2=BC2+BD2，即BC⊥BD，
∵BC⊥BF，且BD∩BF=B，
∴BC⊥平面BFD，
∵EF//BC，∴EF⊥平面BFD，
由(1)知BF⊥平面ADEF，
∵DF⊂平面ADEF，∴DF⊥BF，
故FD，FE，FB两两垂直，
∵BD= 3，FB= 2，∴FD=1，
以F为坐标原点，建立如图所示的空间直角坐标系，
则F(0,0,0)，A(−2,0,1)，B(0, 2,0)，C(1, 2,0)，D(0,0,1)，
∴DC=(1, 2,−1)，FA=(−2,0,1)，FB=(0, 2,0)，
设平面ABF的法向量为n=(x,y,z)，则n⋅FA=0n⋅FB=0，即−2x+z=0 2y=0，
取n=(1,0,2)，
设直线DC与平面ABF所成角为θ，
则sinθ=|cs|=|1−22× 5|= 510，
故直线DC与平面ABF所成角的正弦值为 510．
【解析】(1)先证四边形EFBC为平行四边形，可得BF//EC，结合AD//EF，AD⊥EC，可得BF⊥EF，再利用面面垂直的性质定理，推出BF⊥平面ADEF，从而得证；
(2)先证FD，FE，FB两两垂直，再以F为坐标原点建立空间直角坐标系，利用向量法求直线与平面所成角即可．
20.解：(Ⅰ)当x∈[12,20]时，P=k1x+b1，代入点(12,26)，(20,10)，
得k1=−2，b1=50，∴P=−2x+50；
同理x∈(20,28]时，P=−x+30，
∴周销量P(件)与单价x(元)之间的函数关系式P=−2x+50,12≤x≤20−x+30,20(Ⅱ)y=P(x−10)−25
=(−2x+50)(x−10)−25,12≤x≤20,(−x+30)(x−10)−2520当x∈[12,20]时，y=−2(x−352)2+1752，x=352时，ymax=1752；
x∈(20,28]时，y=−(x−20)2+75，函数单调递减，∴y<75，
综上所述，x=352时，ymax=1752．
【解析】(Ⅰ)根据函数图象，求出解析式，即可写出周销量P(件)与单价x(元)之间的函数关系式；
(Ⅱ)分段求出函数的最值，即可得出结论．
21.解：(1)当a=2时，f(x)=e2x⋅csx，
f′(x)=e2x(2csx−sinx)，
f(0)=1，f′(0)=2，
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=2x+1．
(2)(ⅰ)f′(x)=eax(acsx−sinx)，
当a=0时，f(x)=csx，在区间(0,π)上单调递减，不存在极值点，
当a>0时，在[π2,π)时，acsx−sinx<0，f′(x)<0，
由函数y=tanx的图象及性质，可得存在x1∈(0,π2)，使得tanx1=a，即acsx1−sinx1=0，
所以当x∈(0,x1)时，acsx−sinx>acsx1−sinx1=0，则f′(x)>0，
当x∈(x1,π2)时，acsx−sinx所以f(x)在(0,x1)上单调递增，在(x1,π)上单调递减，在(0,π)上不存在极小值点．
当a<0时，则当x∈(0,π2]时，acsx−sinx<0，则f′(x)<0，
由函数y=tanx的图象和性质，存在t∈(π2,π)，使得tant=a，即acst−sint=0，
所以当x∈(π2,t)时，acsx−sinx当x∈(t,π)时，acsx−sinx>acst−sint=0，则f′(x)>0，
所以f(x)在(0,t)上单调递减，在(t,π)上单调递增，
此时x=t为f(x)在区间(0,π)上的唯一的极小值点，
综上所述，实数a的取值范围为(−∞,0)．
(ⅱ)由(ⅰ)，a<0，f(x)在(0,π)上的唯一的极小值点t满足t∈(π2,π)且tant=a，
由此g(a)=f(t)=eat⋅cst=ettant⋅cst，
令ℎ(x)=extanx⋅csx，x∈(π2,π)，
则g(a)=ℎ(t)，且ℎ′(x)=extanx[(tanx+xcs2x)csx−sinx]=extanx⋅xcsx<0，
所以ℎ(x)在区间(π2,π)上单调递减，
下面证明函数g(a)在区间(−∞,0)上单调递减，
对于任意的a1则t1，t2∈(π2,π)，且tant1=a1，tant2=a2，
由a1又由ℎ(x)在区间(π2,π)上单调递减，
所以g(a1)=ℎ(t1)>ℎ(t2)=g(a2)，
综上所述，对于任意的a1g(a2)，即g(a)在区间(−∞,0)上单调递减．
【解析】(1)当a=2时，f(x)=e2x⋅csx，求导得f′(x)，由导数的几何意义可得切线的斜率f′(0)，则切线的方程为y−f(0)=f′(0)(x−1)，化简即可得出答案．
(2)(ⅰ)求导得f′(x)=eax(acsx−sinx)，分三种情况：当a=0时，当a>0时，当a<0时，分析f′(x)的单调性，极值，即可得出答案．
(ⅱ)由(ⅰ)，a<0，f(x)在(0,π)上的唯一的极小值点t满足t∈(π2,π)且tant=a，则g(a)=f(t)=eat⋅cst=ettant⋅cst，求导分析g(a)的单调性，即可得出答案．

2023-2024学年福建省福州市格致中学高二（下）期末数学试卷（含解析）

更专业

更丰富

更便捷

真低价

欢迎来到教习网