专题06 全等三角形的判定（二）（含答案）【暑假预习课堂】新八年级数学同步精讲精练（人教版）

这是一份专题06 全等三角形的判定（二）（含答案）【暑假预习课堂】新八年级数学同步精讲精练（人教版），文件包含专题06全等三角形的判定二原卷版暑假预习课堂新八年级数学同步精讲精练人教版docx、专题06全等三角形的判定二解析版暑假预习课堂新八年级数学同步精讲精练人教版docx等2份试卷配套教学资源，其中试卷共39页， 欢迎下载使用。

目录
【考点一 直角三角形全等的判定HL】
【考点二 全等三角形的判定和性质】
【考点三 全等三角形的判定和性质的应用】
【聚焦考点1】
1、判定直角三角形全等的一般方法
由三角形全等的条件可知，对于两个直角三角形，满足一边一锐角对应相等，或两直角边对应相等，这两个直角三角形就全等了.这里用到的是“AAS”，“ASA”或“SAS”判定定理.
2、判定直角三角形全等的特殊方法——斜边，直角边定理
在两个直角三角形中，有斜边和一条直角边对应相等的两个直角三角形全等（可以简写成“斜边、直角边”或“HL”）.这个判定方法是直角三角形所独有的，一般三角形不具备.
【典例剖析1】
【典例1-1】如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高．求证Rt△ADE≌Rt△ADF．
【典例1-2】如图，AB⊥BC，AD⊥DC，AB＝AD，求证：∠1＝∠2．
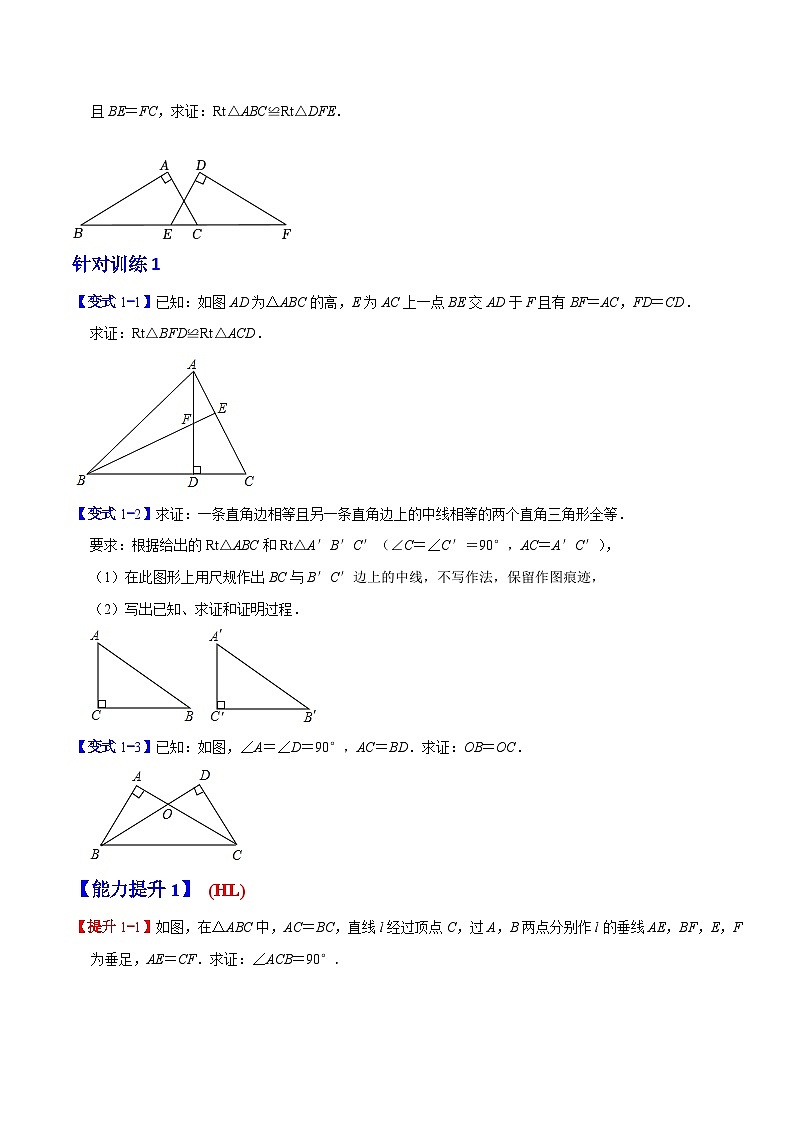
【典例1-3】如图，在△ABC和△DEF中，∠A＝∠D＝90°，AC＝DE，点B、E、C、F在同一条直线上，且BE＝FC，求证：Rt△ABC≌Rt△DFE．
​
针对训练1
【变式1-1】已知：如图AD为△ABC的高，E为AC上一点BE交AD于F且有BF＝AC，FD＝CD．
求证：Rt△BFD≌Rt△ACD．
【变式1-2】求证：一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等．
要求：根据给出的Rt△ABC和Rt△A′B′C′（∠C＝∠C′＝90°，AC＝A′C′），
（1）在此图形上用尺规作出BC与B′C′边上的中线，不写作法，保留作图痕迹，
（2）写出已知、求证和证明过程．
【变式1-3】已知：如图，∠A＝∠D＝90°，AC＝BD．求证：OB＝OC．
【能力提升1】 (HL)
【提升1-1】如图，在△ABC中，AC＝BC，直线l经过顶点C，过A，B两点分别作l的垂线AE，BF，E，F为垂足，AE＝CF．求证：∠ACB＝90°．
【提升1-2】如图，在直角三角形ABC中，∠C＝90°，AC＝20，BC＝10，PQ＝AB，P，Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动，且点P不与点A，C重合，那么当点P运动到什么位置时，才能使△ABC与△APQ全等？
【提升1-3】已知：如图1，在Rt△ABC和Rt△A'B'C'中，AB＝A′B′，AC＝A′C′，C＝∠C′＝90°
求证：Rt△ABC和Rt△A′B′C′全等．
（1）请你用“如果…，那么…”的形式叙述上述命题；
（2）将△ABC和△A′B′C′拼在一起，请你画出两种拼接图形；例如图2：（即使点A与点A′重合，点C与点C′重合．）
（3）请你选择你拼成的其中一种图形，证明该命题．
【聚焦考点2】
1.平移、翻折、旋转前后的两个三角形全等．
2． 全等三角形的性质：（1）全等三角形的对应边相等；（2）全等三角形的对应角相等．
3． 全等三角形的判定方法：
（1）三边对应相等的两个三角形全等（SSS）；
（2）两边和它们的夹角对应相等的两个三角形全等（SAS）；
（3）两角和它们的夹边对应相等的两个三角形全等（ASA）；
（4）两个角和其中一个角的对边对应相等的两个三角形全等（AAS）．
（5）斜边和一条直角边对应相等的两个直角三角形全等（ HL）
【典例剖析2】
【典例2-1】如图，已知D是AC上一点，AB＝AD，AD+DC＝DE，AE＝BC．求证：∠EAD＝∠B．
【典例2-2】如图，点B，E，C，F在同一直线上，∠A＝∠D＝90°，BC＝FE，AB＝DF．求证：∠B＝∠F．
【典例2-3】如图，AB∥EF，AC∥DE，FC＝DB，求证：AB＝EF．
针对训练2
【变式2-1】如图，点B在CD上，OB＝OD，AB＝CD，∠OBA＝∠D；
（1）求证：△ABO≌△CDO；
（2）当AO∥CD，∠BOD＝30°，求∠A的度数．
​
【变式2-2】如图，点D在BC上，∠ADB＝∠B，∠BAD＝∠CAE．
（1）添加条件： AC＝AE （只需写出一个），使△ABC≌△ADE；
（2）根据你添加的条件，写出证明过程．
【变式2-3】如图，在△ABE和△ACF中，∠E＝∠F＝90°，∠B＝∠C，BE＝CF．
求证：（1）∠1＝∠2．
（2）CM＝BN．
​
【能力提升2】
【提升2-1】如图，在△ABC中，∠B＝50°，∠C＝20°．过点A作AE⊥BC，垂足为E，延长EA至点D．使AD＝AC．在边AC上截取AF＝AB，连接DF．求证：DF＝CB．
【提升2-2】如图，已知△ABC中AB＝AC＝12厘米，BC＝9厘米，点D为AB的中点．
（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．①若点P点Q的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点P点Q的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间，点P与点Q第一次在△ABC的哪条边上相遇？此时相遇点距到达点B的路程是多少？
【提升2-3】在△ABC中，AB＝AC，D是边BC上一点，点E在AD的右侧，线段AE＝AD，且∠DAE＝∠BAC＝α．
（1）如图1，若α＝60°，连接CE，DE．则∠ADE的度数为 60° ；BD与CE的数量关系是 BD＝CE ．
（2）如图2，若α＝90°，连接EC、BE．试判断△BCE的形状，并说明理由．
【聚焦考点3】
全等三角形的应用
（1）全等三角形的性质与判定综合应用
用全等寻找下一个全等三角形的条件，全等的性质和判定往往是综合在一起应用的，这需要认真分析题目的已知和求证，分清问题中已知的线段和角与所证明的线段或角之间的联系．
（2）作辅助线构造全等三角形
常见的辅助线做法：①把三角形一边的中线延长，把分散条件集中到同一个三角形中是解决中线问题的基本规律．②证明一条线段等于两条线段的和，可采用“截长法”或“补短法”，这些问题经常用到全等三角形来证明．
（3）全等三角形在实际问题中的应用
一般方法是把实际问题先转化为数学问题，再转化为三角形问题，其中，画出示意图，把已知条件转化为三角形中的边角关系是关键
【典例剖析3】
【典例3-1】如图，数学实践小组想要测量某公园的人工湖两端A、B之间的距离，由于条件限制无法直接测得，请你用学过的数学知识帮他们按以下要求设计一种测量方案．
（1）画出测量示意图；
（2）写出测量的数据，线段长度用a、b、c…表示，角度用α、β、γ…表示；（不要求写出测量过程）
（3）根据你测量的数据，计算A、B之间的距离．（用含a、b、c…或 α、β、γ…的式子表示）
【典例3-2】某建筑测量队为了测量一株居民楼ED的高度，在大树AB与居民楼ED之间的地面上选了一点C，使B，C，D在一直线上，测得大树顶端A的视线AC与居民楼顶墙E的视线EC的夹角为90°，若AB＝CD＝12米，BD＝64米，请计算出该居民楼ED的高度．
【典例3-3】新冠疫情爆发以来，人们都自觉减少外出游玩，小区内的运动器材区成了小朋友运动的最佳场所．如图，某小区内小朋友荡秋千的侧面示意图，静止时秋千位于铅垂线BD上，转轴中心B到地面的距离BD＝3m．在荡秋千过程中，当秋千摆动到最高点A时，测得点A到BD的距离AC＝2m，点A到地面的距离AE＝1.8m；当从A处摆动到A'处时，有A'B⊥AB．
（1）求A'到BD的距离；
（2）求A'到地面的距离．
针对训练3
【变式3-1】为测量一条两岸平行的小河宽度，某班数学研究小组设计了测量方案：
请分析该数学研究小组是否能测量出小河的宽度，并说明理由．
【变式3-2】数学兴趣小组想在不用涉水的情况下测量某段河流的宽度（该段河流两岸是平行的），在数学老师带领下他们是这样做的：
①在河流的一条岸边B点，选对岸正对的一棵树A为参照点；
②沿河岸直走10m有一棵树C，继续前行10m到达D处；
③从D处沿河岸垂直的方向行走，当到达A树正好被C树遮挡住的E处停止行走；
④测得DE的长为4.5m．
（1）河流的宽度为 4.5 m；
（2）请你说明他们做法的正确性．
【变式3-3】如图，A，B两点位于高墙外，不能直接到达．为在该高楼的楼顶上搭建一个支架，需要在地面测量出A，B间的距离．学习了三角形全等知识后，小明给出了如下的方案：先在地面上取一点可以直接到达A点和B点的点O，连接AO并延长到C，使OC＝OA；连接BO并延长到D，使OD＝OB，连接CD并测量出CD的长度，CD的长度就是A，B间的距离．请根据以上的信息，说明AB＝CD．
【能力提升3】
【提升3-1】．池塘两端A，B的距离无法直接测量，请同学们设计方案测量A，B的距离．八年级一班甲，乙两位同学分别设计出了如下两种方案：
甲：如图①，先在平地上取一个可以直接到达点A，B的点O，连接AO并延长到点C，连接BO并延长到点D，使CO＝AO，DO＝BO，连接DC，测出DC的长即可．
乙：如图②，先确定直线AB，过点B作直线BE⊥AB，在直线BE上找可以直接到达点A的一点D，连接DA，作DC＝DA，交直线AB于点C，最后测量BC的长即可．
请分析两种方案可行的理由，
【提升3-2】．如图，某村庄有一块五边形的田地，AB＝AE＝CD＝60m，∠ABC＝∠AED＝90°，连接对角线AC，AD，∠BAE＝2∠CAD．
（1）∠BAC，∠DAE与∠CAD之间的数量关系是 ∠BAC+∠DAE＝∠CAD ．
（2）为保护田内作物不被牲畜踩踏，村里决定给这块田地的五边上围一圈木栅栏，已知每米木栅栏的建造成本是50元，则建造木栅栏共需花费多少元？（提示：延长CB至点G，使BG＝DE）
（3）在△ADE和△ABC区域种上小麦，已知每平方米田地的小麦播种量为11.25克，请直接写出需提前准备多少千克的小麦种．
【提升3-1】．【问题背景】
在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且∠EAF＝60°，试探究图1中线段BE、EF、FD之间的数量关系．
【初步探索】
小亮同学认为：延长FD到点G，使DG＝BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，则可得到BE、EF、FD之间的数量关系是 EF＝BE+FD ．
【探索延伸】
在四边形ABCD中如图2，AB＝AD，∠B+∠D＝180°，E、F分别是BC、CD上的点，∠EAF＝∠BAD，上述结论是否仍然成立？说明理由．
【结论运用】
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角（∠EOF）为70°，试求此时两舰艇之间的距离．
课题
测量小河的宽度
成员
组长：×××组员：×××，×××，×××
测量工具
皮尺，测角仪
测量方案示意图
说明
点A在点B的正北方，AB⊥BF，在BF上取两点C，D，使CD＝BC，再作出BF的垂线DE，使点A，C，E在同一条直线上（如图所示）