2023-2024学年黑龙江省哈尔滨市道外区七年级（下）期末数学试卷（含答案）

这是一份2023-2024学年黑龙江省哈尔滨市道外区七年级（下）期末数学试卷（含答案），共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列方程中是二元一次方程的为( )
A. x+y3=1B. xy=1C. 2x2−1=0D. 2x+2y=1
2.若a>b，则下列式子中错误的是( )
A. a−2>b−2B. a2>b2C. a+2>b+2D. −2a>−2b
3.已知一组数据2，3，5，6，则这组数据的平均数为( )
A. 3B. 4C. 5D. 6
4.下列长度的三条线段能组成三角形的是( )
A. 2cm，3cm，6cmB. 4cm，5cm，9cm
C. 2cm，2cm，5cmD. 3cm，4cm，5cm
5.如图所示，在ABC中，BD平分∠ABC，交AC于点D，若∠A=75°，∠CBD=35°，∠C的度数是( )
A. 40°B. 35°C. 30°D. 45°
6.方程组x+y=my=2x−n的解为x=4y=5，则m、n的值分别为( )
A. 4、5B. 9、3C. 9、−3D. −9、5
7.某校开展“共创文明班，书香满校园”的古诗文朗诵比赛，共有100位同学参加了初赛，按成绩将有50人进入复赛，如果宁宁同学知道了自己的成绩后，要判断自己是否能进入复赛，他需要知道这100位同学成绩的( )
A. 方差B. 众数C. 中位数D. 加权平均数
8.如图，已知：∠AOB.求作：∠A′O′B′，使∠A′O′B′=∠AOB.利用尺规作图方法用到的三角形全等的判定方法是( )
A. AASB. SASC. ASAD. SSS
9.两组邻边分别相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中AB=AD，CB=CD，点O为对角线AC、BD的交点，在探究筝形性质时，我们得到以下结论：①图中有三对全等三角形.②AC、BD互相平分.③S△BCD=12AC⋅BD.其中错误的结论有( )
A. 0个
B. 1个
C. 2个
D. 3个
二、填空题：本题共9小题，每小题3分，共27分。
10.把方程2x+y=40，化成用含x的代数式表示y的形式，则y= ______．
11.三角形的外角和是______．
12.x的2倍与5的差不小于3，用不等式表示为______．
13.不等式组x>−2x≤3的负整数解是______．
14.如果a、b、c为一个三角形的三边，那么点P(−2,a+b−c)在第______象限．
15.若方程mx−y=3的一个解是x=−2y=1，则m= ______．
16.如图，在△ABC中，∠ABC=80°，∠A=30°，D是AC上一点将△ABC沿BD折叠，使C点落在AB边上的点C′处，则∠ADC′= ______°.
17.如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形.如图，就是一组正多边形，根据每个正多边形中∠α的变化情况，可以求得正十边形∠α度数为______°.
18.如图，在△ABC中，CD⊥AB于点D，BE⊥BC交CD延长线于点E，若EC=AB，△ABC的面积是8.则BC= ______．
三、解答题：本题共9小题，共66分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题5分)
解方程组2x+y=54x+3y=7．
20.(本小题5分)
解不等式组并在数轴上表示解集：x+12≥13x−1≤9
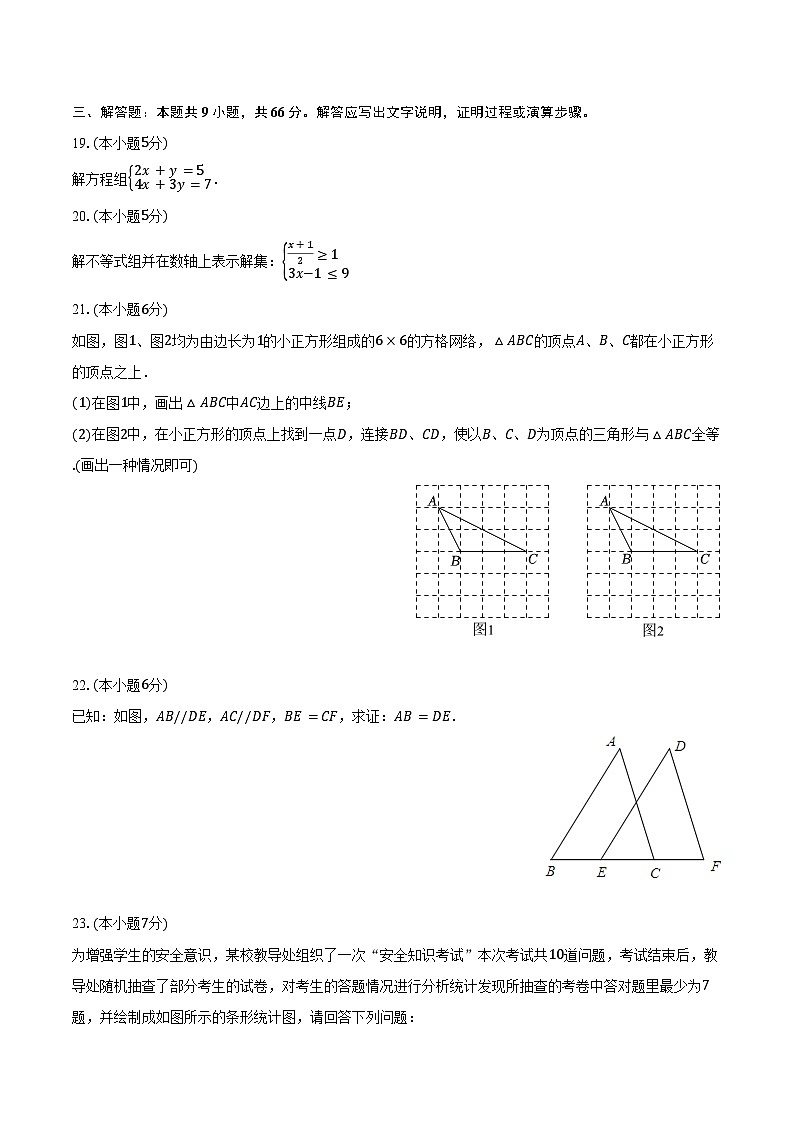
21.(本小题6分)
如图，图1、图2均为由边长为1的小正方形组成的6×6的方格网络，△ABC的顶点A、B、C都在小正方形的顶点之上．
(1)在图1中，画出△ABC中AC边上的中线BE；
(2)在图2中，在小正方形的顶点上找到一点D，连接BD、CD，使以B、C、D为顶点的三角形与△ABC全等.(画出一种情况即可)
22.(本小题6分)
已知：如图，AB//DE，AC/​/DF，BE=CF，求证：AB=DE．
23.(本小题7分)
为增强学生的安全意识，某校教导处组织了一次“安全知识考试”本次考试共10道问题，考试结束后，教导处随机抽查了部分考生的试卷，对考生的答题情况进行分析统计发现所抽查的考卷中答对题里最少为7题，并绘制成如图所示的条形统计图，请回答下列问题：
(1)教导处抽查了______名考生的试卷；
(2)抽查的这部分考生每人答对题数的众数是：______；
(3)如果该校共有学生2000人，答对题目不少于8道为优秀，请你估计该校本次考试成绩为优秀的学生大约有多少人．
24.(本小题7分)
定义一种新的运算f：f(x)=kx+b(k、b为常数，k≠0)这里等式的右侧为通常的四则运算，例如f(2)=2k+b．
(1)已知：f(3)=−1，f(−3)=−3，求k、b的值；
(2)在(1)的条件下，若f(m)=2m，求m的值．
25.(本小题10分)
某机械加工厂甲、乙两个车间承担生产同一种零件的任务，两车间共有50人，甲车间平均每人每天生产零件30个，乙车间平均每人每天生产零件20个，两车间每天生产的零件总数为1300个．
(1)甲、乙两个车间各有多少人？
(2)该厂改进了生产技术，在甲、乙两车间总人数不变的情况下，从甲车间调出一部分人到乙车间，调整后甲车间平均每人每天生产零件35个，乙车间平均每人每天生产零件25个，若调整后两车间每天生产零件的总数不少于1480个，求甲车间最多调出多少人到乙车间？
26.(本小题10分)
如图，在平面直角坐标系中，点O为坐标原点，点A(m,0)，B(0,2m)连接AB，m为不等式组2m+4>814−3m>2的整数解．

(1)点A的坐标为______；点B的坐标为______；
(2)点C(t,0)在x轴负半轴上，连接BC，用含t的代数式表示△ABC的面积S；
(3)在(2)的条件下，若CD⊥AB，垂足为点D，OD平分∠AOB，求△ABC的面积．
27.(本小题10分)
如图1，已知：在△ACB与△DCE中，AC=BC，CD=CE，∠ACB=∠DCE，连接AD、BE．

(1)求证：AD=BE；
(2)如图2，已知AD、BE交点为F，连接CF，求证：FC平分∠AFE；
(3)如图3在(2)的条件下，若∠ACB=90°，作AG⊥FC，交FC延长线于点G，AC平分∠GAF，且△ACF的面积为36，求AC的长度．
参考答案
1.A
2.D
3.B
4.D
5.B
6.B
7.C
8.D
9.C
10.−2x+40
11.360°
12.2x−5≥3
13.−1
14.二
15.−2
16.40
17.18
18.4
19.解：2x+y=5 ①4x+3y=7②，
①×3−②得：2x=8，
解得：x=4，
把x=4代入①得，8+y=5，
解得：y=−3，
则原方程组的解为x=4y=−3．
20.解：解不等式x+12≥1，得：x≥1，
解不等式3x−1≤9，得：x≤103，
则不等式组的解集为1≤x≤103，
将解集表示在数轴上如下：

21.解：(1)如图1中，中线BE即为所求；
(2)如图2中，△BCD即为所求(答案不唯一)．

22.证明：∵AB//DE，
∴∠B=∠DEF．
∵AC/​/DF，
∴∠ACB=∠F，
∵BE=CF，
∴BE+EC=EC+CF，
即BC=EF，
在△ABC和△DEF中，∠B=∠DEFBC=EF∠ACB=∠F，
∴△ABC≌△DEF(ASA)，
∴AB=DE．
23.(1)20；
(2)8；
(3)2000×8+6+220=1600(人)，
答：估计该校本次考试成绩优秀的学生大约有1600人．
24.解：(1)由f(3)=−1得3k+b=−1，
由f(−3)=−3得−3k+b=−3，
联立得3k+b=−1−3k+b=−3，
解得：k=13b=−2；
(2)由(1)得f(x)=13x−2，
∵f(m)=2m，
∴13m−2=2m，
解得m=−65
25.解：(1)设甲车间有x人，乙车间有y人，由题意得，
x+y=5030x+20y=1300，
解得：x=30y=20，
答：甲车间有30人，乙车间有20人．
(2)设从甲车间调出a人到乙车间，则甲车间有(30−a)人，乙车间有(20+a)人，
35(30−a)+25(20+a)≥1480，
解得：a≤7，
答：从甲车间最多调出7人到乙车间．
26.(1)(3,0)，(0,6)；
(2)①∵点C(t,0)，
∴AC=3−t，
∴S△ABC=12AC×OB=9−3t；
(3)作DE⊥x轴于点E，DF⊥y轴于点F，
∵OD平分∠AOB，
∴DE=DF，
∵S△AOB=S△AOD+S△BOD，
12×3×6=12×3DE+12×6DF，
∴DE=DF=2，
∴D(2,2)
∵CD⊥AB，
∴∠CDB=∠CDA=∠AOB=90°，
∴∠ABO+∠BAO=∠BAO+∠CAD=90°，
∴∠ABO=∠ACD，
∴△BDF≌△CDE(AAS)，
∴CE=BF=6−2=4，
∴OC=2，
∴AC=OC+OA=6，
∴△ABC面积为12AC⋅OB=12×5×6=15．
27.(1)证明：∵∠ACB=∠DCE，
∴∠ACB+∠BCD=∠DCE+∠BCD，
即∠ACD=∠BCE，
在△ACD与△BCE中，
AC=BC∠ACD=∠BCECD=CE，
∴△ACD≌△BCE(SAS)，
∴AD=BE；
(2)证明：作CM⊥AD于点M，作CN⊥BE于点N，

∴∠AMC=∠BNC=90°，
由(1)得△ACD≌△BCE，
∴∠CAM=∠CBN，
又∵AC=BC，
∴△ACM≌△BCN(AAS)，
∴CM=CN，
∴CF平分∠AFE；
(3)解：∵∠AFC=∠FCD+∠FDC，
∴∠AFE=∠AFC+∠EFC=∠ADC+∠CDE+∠DEB
=∠BEC+∠BED+∠CDE
=180°−∠ECD=90°，

作CM⊥AD于M，CN⊥BE于N，
∴∠AMC=∠BNC=90°，
∵△ACD≌△BCE，
∴∠CAD=∠CBN，
∵AC=BC，
∴△ACM≌△BCN(AAS)，
∴CM=CN，
∴CF平分∠AFE，
∴∠ACG=45°，
∴△AGF是等腰直角三角形，
∴AG=FG，
作FP⊥AC于点P，交AG延长线于点Q，
∵AC平分∠GAF，
∴∠QAP=∠FAP，
∵∠APQ=∠APF，AP=AP，
∴△AFP≌△AQP(ASA)，
∴PQ=PF，
∴QF=2FP，
∵AG⊥FG，
∴∠AGF=∠FPC=90°，
∵∠ACG=∠FCP，
∴∠GAC=∠CFP，
∴△FGQ≌△AGC(ASA)，
∴AC=FQ，
∴S△ACF=12AC⋅PF=12×2FP⋅FP=36，
∴FP=6，
∴AC=2FP=12．
作法：①以点O为圆心，任意长为半径画弧，交OA、OB于点C、D；
②画一条射线O′A′，以点O′为圆心，长为半径画弧，交O′A′于点C′；
③以点C′为圆心，CD长为半径画弧，与前弧交于点D′；
④过点D′画射线O′B′．
则∠A′O′B′=∠AOB．