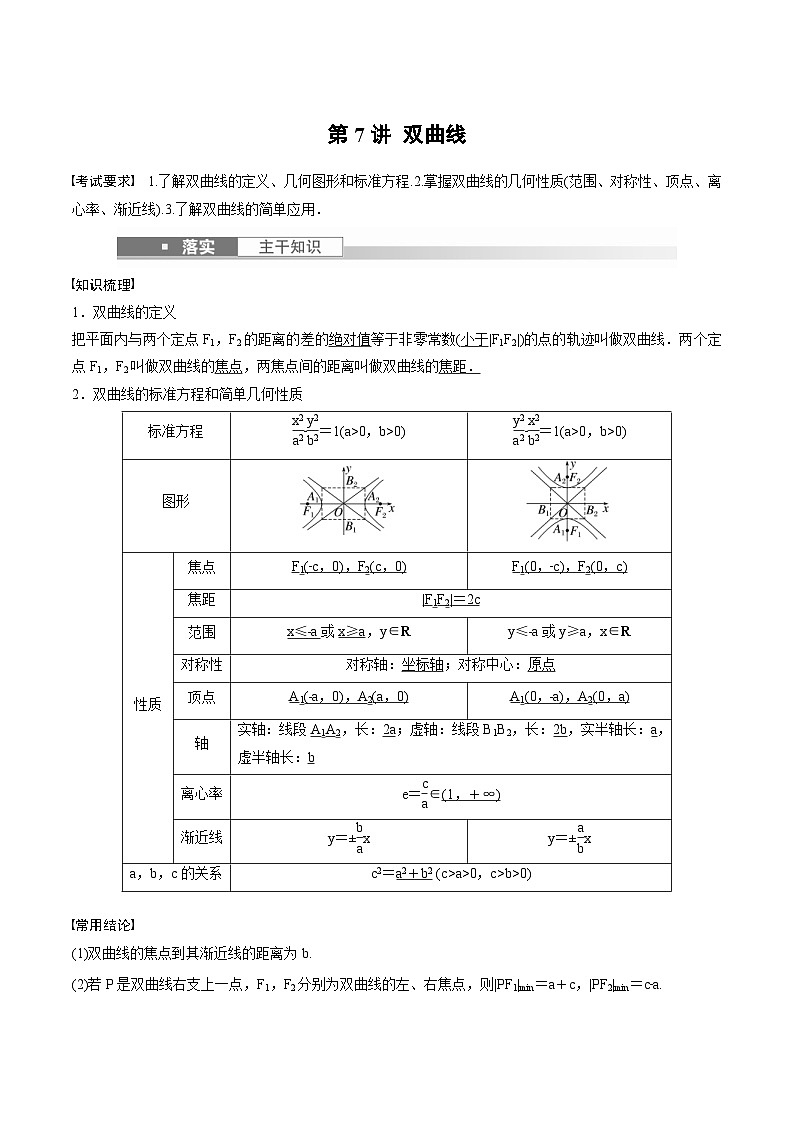
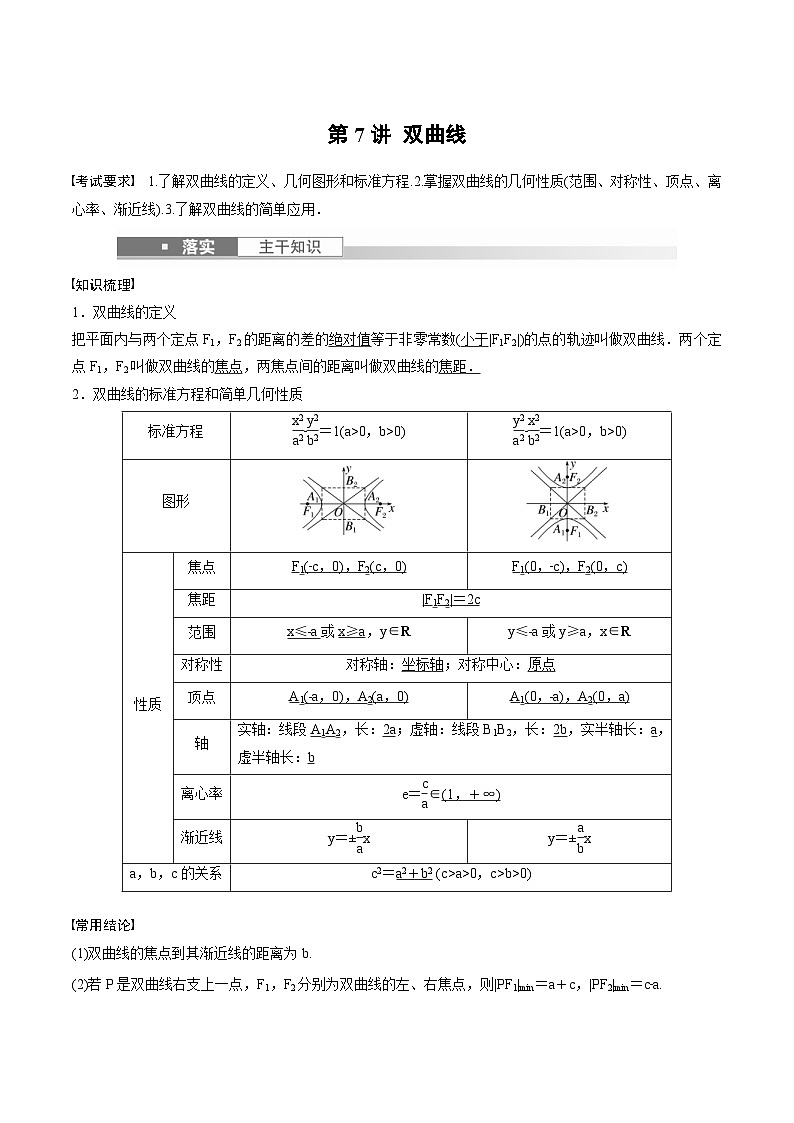
2024年高二数学暑期培优讲义 第07讲 双曲线+课后巩固练习（2份打包，原卷版+教师版）

这是一份2024年高二数学暑期培优讲义 第07讲 双曲线+课后巩固练习（2份打包，原卷版+教师版），文件包含2024年高二数学暑期培优讲义第07讲双曲线教师版doc、2024年高二数学暑期培优讲义第07讲双曲线教师版pdf、2024年高二数学暑期培优讲义第07讲双曲线课后巩固练习教师版doc、2024年高二数学暑期培优讲义第07讲双曲线课后巩固练习教师版pdf、2024年高二数学暑期培优讲义第07讲双曲线学生版doc、2024年高二数学暑期培优讲义第07讲双曲线学生版pdf、2024年高二数学暑期培优讲义第07讲双曲线课后巩固练习学生版doc、2024年高二数学暑期培优讲义第07讲双曲线课后巩固练习学生版pdf等8份试卷配套教学资源，其中试卷共60页， 欢迎下载使用。

1.渐进线方程为x±y＝0的双曲线的离心率是( )
A.eq \f(\r(2),2) B.1 C.eq \r(2) D.2
答案为：C.解析：根据渐进线方程为x±y＝0的双曲线，可得a＝b，所以c＝eq \r(2)a
则该双曲线的离心率为e＝eq \f(c,a)＝eq \r(2)，故选C.]
2.若实数k满足0＜k＜9，则曲线eq \f(x2,25)﹣eq \f(y2,9－k)＝1与曲线eq \f(x2,25－k)﹣eq \f(y2,9)＝1的( )
A.离心率相等 B.虚半轴长相等
C.实半轴长相等 D.焦距相等
答案为：D.解析：由0＜k＜9，易知两曲线均为双曲线且焦点都在x轴上，由eq \r(25＋9－k)＝eq \r(25－k＋9)，得两双曲线的焦距相等.]
3.已知抛物线y2＝4x的焦点为F，准线为l.若l与双曲线eq \f(x2,a2)﹣eq \f(y2,b2)＝1(a>0，b>0)的两条渐近线分别交于点A和点B，且|AB|＝4|OF|(O为原点)，则双曲线的离心率为( )
A.eq \r(2) B.eq \r(3) C.2 D.eq \r(5)
答案为：D.解析：l的方程为x＝﹣1，双曲线的渐近线方程为y＝±eq \f(b,a)x，故得A(﹣1，eq \f(b,a))，B(﹣1，﹣eq \f(b,a))，所以eq \b\lc\|\rc\|(\a\vs4\al\c1(AB))＝eq \f(2b,a)，eq \f(2b,a)＝4，b＝2a，所以e＝eq \f(c,a)＝eq \f(\r(a2＋b2),a)＝eq \r(5)，故选D.]
4.已知点A(﹣1，0)，B(1，0)为双曲线eq \f(x2,a2)﹣eq \f(y2,b2)＝1(a＞0，b＞0)的左、右顶点，点M在双曲线上，△ABM为等腰三角形，且顶角为120°，则该双曲线的标准方程为( )
A.x2﹣eq \f(y2,4)＝1 B.x2﹣eq \f(y2,3)＝1 C.x2﹣eq \f(y2,2)＝1 D.x2﹣y2＝1
答案为：D.解析：由题意知a＝1.不妨设点M在第一象限，则由题意有|AB|＝|BM|＝2，∠ABM＝120°.过点M作MN⊥x轴于点N，则|BN|＝1，|MN|＝eq \r(3)，所以M(2，eq \r(3))，代入双曲线方程得4﹣eq \f(3,b2)＝1，解得b＝1，所以双曲线的方程为x2﹣y2＝1，故选D.]
5.已知△ABC的顶点A(﹣5，0)，B(5，0)，△ABC内切圆的圆心在直线x＝2上，则顶点C的轨迹方程是( )
A.eq \f(x2,4)﹣eq \f(y2,21)＝1(x＞2) B.eq \f(y2,4)﹣eq \f(x2,21)＝1(y＞2)
C.eq \f(x2,21)﹣eq \f(y2,4)＝1 D.eq \f(y2,4)﹣eq \f(x2,2)＝1
答案为：A.解析：如图，△ABC与内切圆的切点分别为G，E，F.|AG|＝|AE|＝7，|BF|＝|BG|＝3，|CE|＝|CF|，所以|CA|﹣|CB|＝7﹣3＝4.根据双曲线定义，所求轨迹是以A，B为焦点，实轴长为4的双曲线的右支，方程为eq \f(x2,4)﹣eq \f(y2,21)＝1(x＞2).]
6.过双曲线eq \f(x2,a2)﹣eq \f(y2,b2)＝1(a＞0，b＞0)的左、右焦点分别作双曲线的两条渐近线的平行线，若这4条直线所围成的四边形的周长为8b，则该双曲线的渐近线方程为( )
A.y＝±x B.y＝±eq \r(2)x C.y＝±eq \r(3)x D.y＝±2x
答案为：A.解析：由双曲线的对称性得该四边形为菱形，因为该四边形的周长为8b，所以菱形的边长为2b，由勾股定理得4条直线与y轴的交点到x轴的距离为eq \r(4b2－c2)＝eq \r(3b2－a2)，又4条直线分别与两条渐近线平行，所以eq \f(b,a)＝eq \f(\r(3b2－a2),\r(a2＋b2))，解得a＝b，所以该双曲线的渐近线的斜率为±1，所以该双曲线的渐近线方程为y＝±x，故选A.]
7.已知双曲线C：eq \f(x2,a2)﹣eq \f(y2,b2)＝1(a>0，b>0)的离心率为2，左、右焦点分别为F1，F2，点A在双曲线C上，若△AF1F2的周长为10a，则△AF1F2的面积为( )
A.2eq \r(15)a2 B.eq \r(15)a2 C.30a2 D.15a2
答案为：B.解析：由双曲线的对称性不妨设A在双曲线的右支上，由e＝eq \f(c,a)＝2，得c＝2a，∴△AF1F2的周长为|AF1|＋|AF2|＋|F1F2|＝|AF1|＋|AF2|＋4a，又△AF1F2的周长为10a，∴|AF1|＋|AF2|＝6a，又∵|AF1|﹣|AF2|＝2a，∴|AF1|＝4a，|AF2|＝2a，在△AF1F2中，|F1F2|＝4a，
∴cs ∠F1AF2＝eq \f(|AF1|2＋|AF2|2－|F1F2|2,2|AF1|·|AF2|)＝eq \f(（4a）2＋（2a）2－（4a）2,2×4a×2a)＝eq \f(1,4).
又0<∠F1AF<π，∴sin ∠F1AF2＝eq \f(\r(15),4)，
∴S△AF1F2＝eq \f(1,2)|AF1|·|AF2|·sin ∠F1AF2＝eq \f(1,2)×4a×2a×eq \f(\r(15),4)＝eq \r(15)a2.]
二、填空题
8.已知双曲线eq \f(x2,a2)﹣eq \f(y2,b2)＝1(a>0，b>0)的一条渐近线为2x＋y＝0，一个焦点为(eq \r(5)，0)，则a＝________；b＝________.
1 2 解析：[由2x＋y＝0，得y＝﹣2x，所以eq \f(b,a)＝2.又c＝eq \r(5)，a2＋b2＝c2，解得a＝1，b＝2.]
9.若双曲线中心在原点，焦点在坐标轴上，离心率为eq \r(2)，且过点(4，﹣eq \r(10))，则该双曲线的标准方程为________.
eq \f(x2,6)﹣eq \f(y2,6)＝1 解析：[依题意，e＝eq \r(2)⇒a＝b.设方程为eq \f(x2,m)﹣eq \f(y2,m)＝1，则eq \f(16,m)﹣eq \f(10,m)＝1，
解得m＝6.∴eq \f(x2,6)﹣eq \f(y2,6)＝1.]
10.设双曲线x2﹣eq \f(y2,3)＝1的左、右焦点分别为F1，F2，若点P在双曲线上，且△F1PF2为锐角三角形，则|PF1|＋|PF2|的取值范围是________.
(2eq \r(7)，8) 解析：[如图，由已知可得a＝1，b＝eq \r(3)，c＝2，从而|F1F2|＝4，由对称性不妨设P在右支上，设|PF2|＝m，则|PF1|＝m＋2a＝m＋2，由于△PF1F2为锐角三角形，结合实际意义需满足eq \b\lc\{(\a\vs4\al\c1(（m＋2）211.已知椭圆eq \f(x2,4)＋eq \f(y2,m)＝1与双曲线x2﹣eq \f(y2,n)＝1的离心率分别为e1，e2，且有公共的焦点F1，F2，则4eeq \\al(2,1)﹣eeq \\al(2,2)＝________，若P为两曲线的一个交点，则|PF1|·|PF2|＝________.
0 3 解析：[由题意得椭圆的半焦距满足ceq \\al(2,1)＝4﹣m，双曲线的半焦距满足ceq \\al(2,2)＝1＋n，
又因为两曲线有相同的焦点，所以4﹣m＝1＋n，即m＋n＝3，
则4eeq \\al(2,1)﹣eeq \\al(2,2)＝4×eq \f(4－m,4)﹣(1＋n)＝3﹣(m＋n)＝0.
不妨设F1，F2分别为两曲线的左、右焦点，点P为两曲线在第一象限的交点，
则eq \b\lc\{(\a\vs4\al\c1(|PF1|＋|PF2|＝4，,|PF1|－|PF2|＝2.))解得eq \b\lc\{(\a\vs4\al\c1(|PF1|＝3，,|PF2|＝1，)) 则|PF1|·|PF2|＝3.]