第09讲 等腰三角形与等边三角形（2大知识点+13大典例+变式训练+随堂检测）-（暑期衔接课堂）2024年暑假七升八数学衔接讲义（人教版）

这是一份第09讲 等腰三角形与等边三角形（2大知识点+13大典例+变式训练+随堂检测）-（暑期衔接课堂）2024年暑假七升八数学衔接讲义（人教版），文件包含第09讲等腰三角形与等边三角形2大知识点+13大典例+变式训练+随堂检测原卷版docx、第09讲等腰三角形与等边三角形2大知识点+13大典例+变式训练+随堂检测解析版docx等2份试卷配套教学资源，其中试卷共182页， 欢迎下载使用。
题型一 等边对等角
题型二 根据等边对等角证明
题型三 根据三线合一证明
题型四 格点图中画等腰三角形
题型五 根据等角对等边证明等腰三角形
题型六 根据等角对等边证明边相等
题型七 根据等角对等边求边长
题型八 直线上与已和两点组成等腰三角形的点
题型九 作等腰三角形(尺规作园)
题型十 等腰三角形的性质和判定
题型十一 等腰三角形的定义
题型十二 等边三角形的判定和性质
题型十三 含30度角的直角三角形
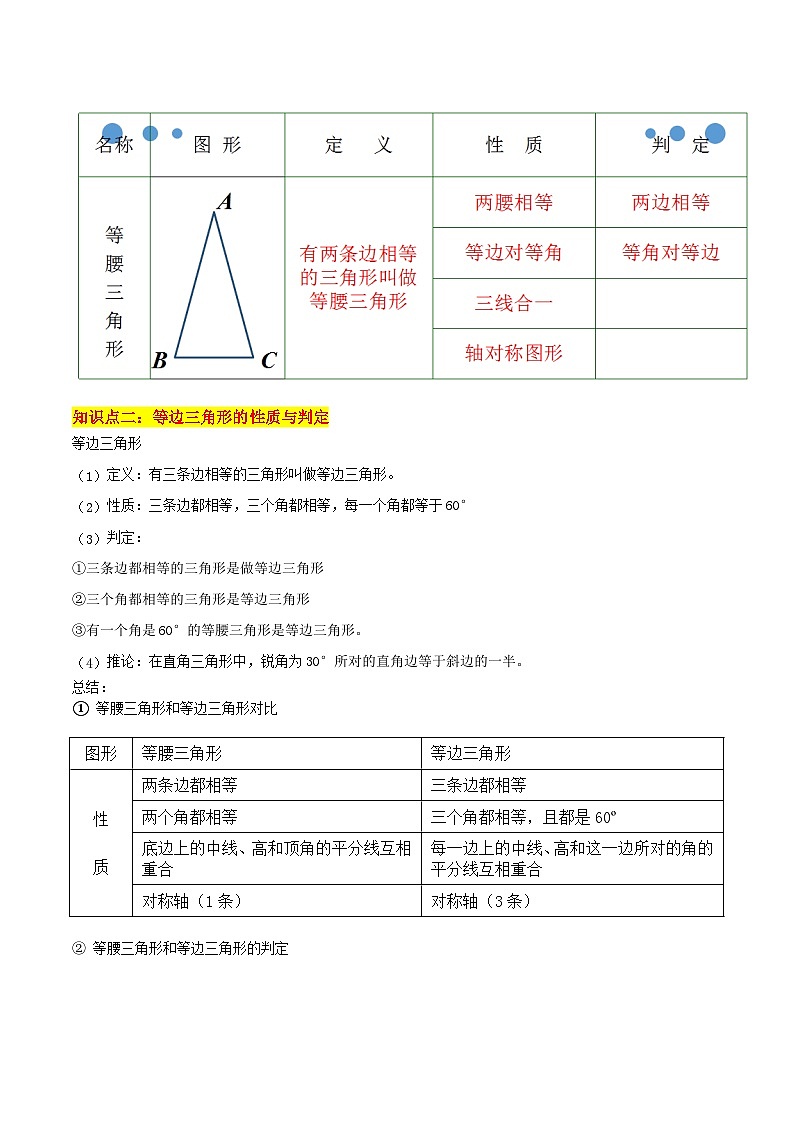
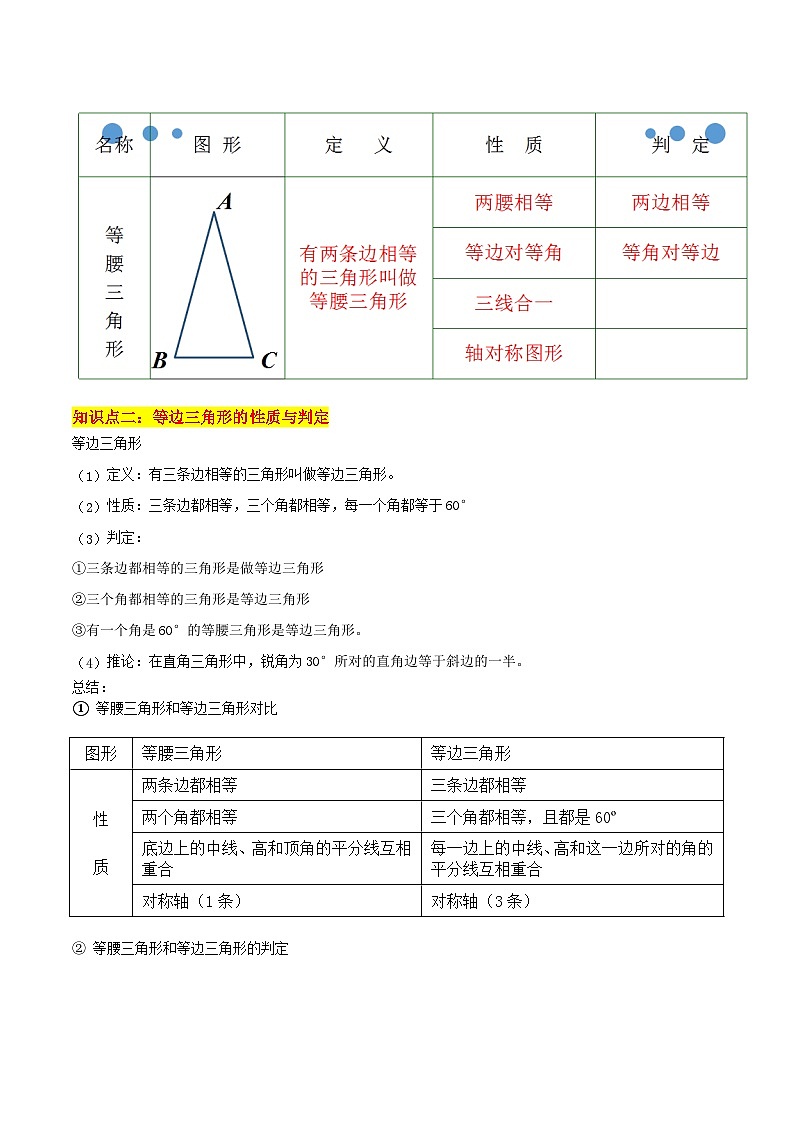
知识点一：等腰三角形的性质
1、等腰三角形
（1）定义：有两条边相等的三角形叫做等腰三角形，相等的两边叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。
（2）性质
①两腰相等
②两底角相等（简称等边对等角）
③等腰三角形顶角平分线、底边上的中线、底边上的高线互相重合（简称为“三线合一”）
④等腰三角形是轴对称图形，其顶角平分线、底边上的中线、底边上的高线所在的直线式对称轴。
证明题目中的写法：
①已知高线：∵AB=AC，AD⊥BC，∴BD=CD，∠BAD=∠CAD
②已知中线：∵AB=AC，BD=CD，∴AD⊥BC，∠BAD=∠CAD
③已知角平分线：∵AB=AC，∠BAD=∠CAD，∴AD⊥BC，BD=CD
（3）等腰三角形的构造
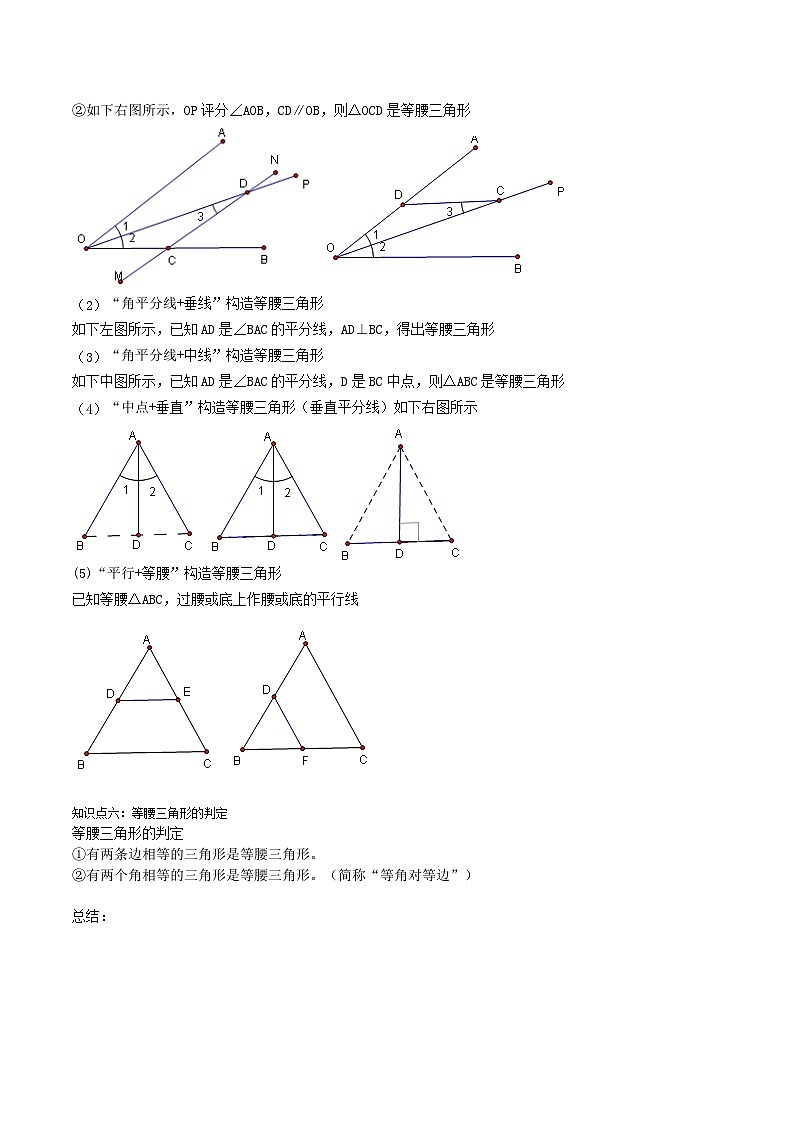
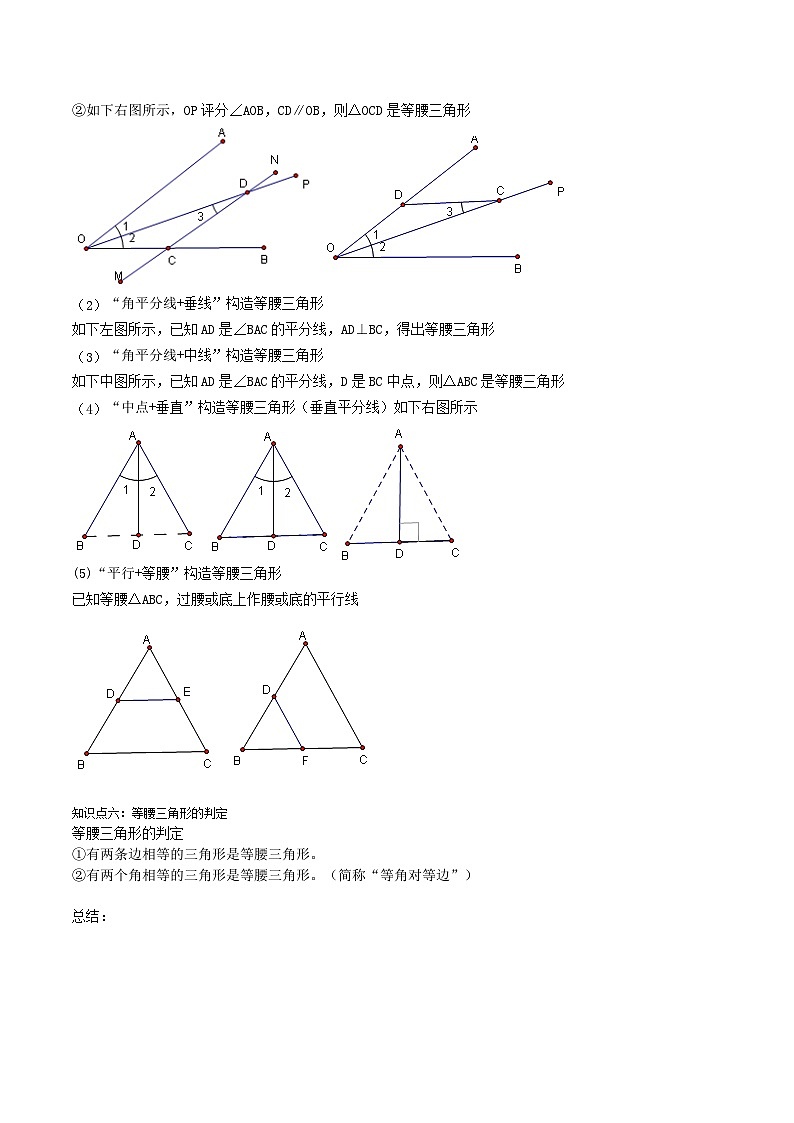
“角平分线+平行线”构造等腰三角形
①如下左图所示，OP评分∠AOB，CD∥OA，则△OCD是等腰三角形
②如下右图所示，OP评分∠AOB，CD∥OB，则△OCD是等腰三角形
“角平分线+垂线”构造等腰三角形
如下左图所示，已知AD是∠BAC的平分线，AD⊥BC，得出等腰三角形
“角平分线+中线”构造等腰三角形
如下中图所示，已知AD是∠BAC的平分线，D是BC中点，则△ABC是等腰三角形
“中点+垂直”构造等腰三角形（垂直平分线）如下右图所示
(5)“平行+等腰”构造等腰三角形
已知等腰△ABC，过腰或底上作腰或底的平行线
知识点六：等腰三角形的判定
等腰三角形的判定
①有两条边相等的三角形是等腰三角形。
②有两个角相等的三角形是等腰三角形。（简称“等角对等边”）
总结：
知识点二：等边三角形的性质与判定
等边三角形
定义：有三条边相等的三角形叫做等边三角形。
性质：三条边都相等，三个角都相等，每一个角都等于60°
判定：
①三条边都相等的三角形是做等边三角形
②三个角都相等的三角形是等边三角形
③有一个角是60°的等腰三角形是等边三角形。
推论：在直角三角形中，锐角为30°所对的直角边等于斜边的一半。
总结：
等腰三角形和等边三角形对比
② 等腰三角形和等边三角形的判定
【典型例题一 等边对等角】
1．（23-24八年级上·河南许昌·期中）等腰三角形的一个底角为，则这个等腰三角形的顶角为（ ）．
A．B．C．D．或
2．（23-24八年级上·广西南宁·阶段练习）等腰三角形的顶角是，那么它的底角是（ ）
A．B．C．D．
3．（23-24八年级上·湖南张家界·期末）已知等腰三角形一底角为，则这个等腰三角形顶角的大小是 度．
4．（23-24八年级上·浙江绍兴·期末）如图，在中，，，则 ．
5．（22-23八年级上·福建福州·期中）如图，在中，，，求的度数．
6．（2023·陕西西安·模拟预测）如图，已知中，，．请用尺规作图法，在上找一点，使得．（保留作图痕迹，不写作法）

【典型例题二 根据等边对等角证明】
1．（22-23八年级下·广东深圳·期末）等腰中，，用尺规作图作出线段BD，则下列结论错误的是（ ）
A．B．C．D．的周长
2．（23-24八年级上·四川宜宾·期末）如图，在中，，D是的中点，下列结论不一定正确的是（ ）
A．B．C．D．
3．（2023八年级上·江苏·专题练习）如图，已知中，，点D为的中点，如果点M在线段上以2厘米/秒的速度由B点向C点运动，同时，点N在线段上由C点向A点运动，若使与全等，则点N的运动速度应为 厘米/秒．
4．（23-24八年级上·湖南长沙·阶段练习）如图，把一张长方形纸片沿对角线折叠，点的对应点为点，与交于点．若长方形的周长为，则的周长为 ．

5．（23-24八年级上·浙江宁波·阶段练习）如图，在中，，D是内一点，且．求证：．
6．（23-24八年级上·河南周口·阶段练习）如图，，，连接交于点O，．求证：．
【典型例题三 根据三线合一证明】
1．（2024·云南昭通·二模）如图，在中，，平分，若，则（ ）
A．10B．12C．5D．6
2．（2024·河北唐山·二模）如图，将折叠，使点C边落在边上，展开得到折痕m，则m是的（ ）

A．中线B．中位线C．角平分线D．高
3．（23-24八年级上·福建厦门·期中）如图，在中，，，为顶角平分线，则 ．

4．（22-23七年级下·全国·课后作业）如图，，若AD平分，则AD与BC的位置关系是 ．
5．（22-23八年级上·全国·单元测试）在中，，是中线，的周长为，的周长为，求的长．
6．（22-23八年级上·全国·课后作业）如图，在中，，点D在上．
(1)若，则_______________．
(2)若，则_______________．
(3)若，则 _______________．
【典型例题四 格点图中画等腰三角形】
1．（22-23八年级上·辽宁盘锦·期末）如图所示的正方形网格中，网格线的交点称为格点．已知A、B是两格点，如果C也是图中的格点，且使得为轴对称图形，则点C的个数是（ ）
A．6B．7C．8D．9
2．（23-24八年级上·吉林四平·期末）如图所示的正方形网格中，网格线的交点称为格点．已知A、是两格点，如果点也是图中的格点，且使得为等腰直角三角形，则点的个数是（ ）
A．个B．个C．个D．个
3．（23-24八年级下·全国·假期作业）如图，的顶点均在正方形网格的格点上，则 ．
4．（22-23八年级上·浙江宁波·阶段练习）在如图所示的方格中，以为边，第三个顶点也在格点上的等腰三角形有 个．

5．（22-23八年级上·浙江温州·期中）如图，在正方形网格中，的顶点均在格点上．
(1)请在图中作出关于直线成轴对称的．
(2)在线段上找一点（点在格点上），使得为等腰三角形．
6．（22-23八年级上·吉林长春·期末）图①、图②是的正方形网格，、两点均在格点上.在图①、图②中各画一个顶点在格点、以为一边的等腰三角形，且所画两个三角形不全等.
图①图②
【典型例题五 根据等角对等边证明等腰三角形】
1．（22-23八年级下·宁夏中卫·开学考试）下列条件中，不能判定是等腰三角形的是（ ）
A． B．C． ，D．
2．（22-23八年级上·黑龙江哈尔滨·阶段练习）如图，在中，，AD平分，，，则（ ）
A．3B．4C．5D．6
3．（22-23八年级上·全国·课后作业）等腰三角形的判定定理：如果一个三角形有 角相等，那么这个三角形是等腰三角形．
4．（22-23八年级上·吉林白城·期中）如图，∠A＝36°，∠DBC＝36°，∠C＝72°，则图中等腰三角形有 个．
5．（22-23八年级上·浙江温州·阶段练习）已知：如图，DB⊥AB，DC⊥AC，∠1＝∠2．求证：AD平分∠BAC．
6．（22-23八年级上·湖北黄石·期末）如图，已知点A、C分别在∠GBE的边BG、BE上，且AB＝AC，AD//BE，∠GBE的平分线与AD交于点D，连接CD．
（1）求证：①AB＝AD；②CD平分∠ACE．
（2）猜想∠BDC与∠BAC之间有何数量关系？并对你的猜想加以证明．
【典型例题六 根据等角对等边证明边相等】
1．（22-23八年级上·陕西渭南·期中）在中，，则（ ）
A．B．C．D．
2．（23-24八年级下·陕西西安·期中）如图是一个跷跷板的示意图，立柱与地面垂直（于点C），跷跷板的一头A着地时，点A、C、在同一水平线上，，若，则的长度为（ ）
A．B．C．D．
3．（23-24八年级上·河北廊坊·期末）在中，，要使为等腰三角形，写出一个可添加的条件： ．
4．（23-24七年级上·山东泰安·期中）如图，在中，的垂直平分线交于点，交于点，．若，则的长是 ．
5．（22-23八年级上·江苏连云港·阶段练习）如图△ABC中，BD、CD分别平分∠ABC，∠ACB，过点D作EF//BC交AB、AC于点E、F，试说明 BE+CF=EF的理由.
6．（22-23七年级上·山东东营·阶段练习）如图所示，四边形的对角线、相交于点，已知，．求证：
(1)；
(2)．
【典型例题七 根据等角对等边求边长】
1．（23-24八年级上·四川乐山·期末）如图，在中，，的垂直平分线交于点，若，，则的周长等于（ ）
A．4cmB．6cmC．8cmD．10cm
2．（23-24八年级下·陕西·期中）如图是一个跷跷板的示意图，立柱与地面垂直（于点C），跷跷板的一头A着地时，当跷跷板的另一头B在处着地时，点A、C、在同一水平线上，，若，则的长度（ ）
A．1.5mB．2mC．2.5mD．3m
3．（22-23八年级上·山东德州·期中）如图，△ABC中，BO、CO分别平分∠ABC、∠ACB，OM∥AB，ON∥AC，BC＝10cm，则ΔOMN的周长为 ．
4．（23-24八年级下·甘肃酒泉·期中）如图，上午9时，一条船从A处出发，以20海里/时的速度向正北航行，11时到达B处，从A，B处望灯塔C，测得，，那么从B处到灯塔C的距离是 海里．

5．（22-23八年级下·陕西咸阳·阶段练习）如图，在中，，若，求的周长．

6．（23-24八年级上·广西南宁·期中）如图，上午8时，一条船从海港出发，以15海里/小时的速度向正北航行，11时到达海岛处，从海港，海岛处望灯塔，分别测得，．

(1)求海岛与灯塔之间的距离；
(2)若该船每海里耗油0.5升，油箱容量为40升，求该船当天装满油箱从海港A出发到海岛B，再从海岛B去到灯塔C的过程中至少还需补充多少升油？
【典型例题八 直线上与已和两点组成等腰三角形的点】
1．（2024·贵州毕节·一模）点A，B在直线l同侧，若点C是直线l上的点，且是等腰三角形，则这样的点C最多有（ ）
A．5个B．4个C．3个D．2个
2．（23-24八年级上·江苏盐城·期末）在平面直角坐标系中，已知点，在y轴上确定点B，使为等腰三角形，符合条件的点B共有（ ）
A．4个B．3个C．2个D．1个
3．（23-24八年级上·河北沧州·阶段练习）如图所示，用两根钢索加固直立的电线杆，若要使钢索与的长度相等，需加条件 ，理由是 ．
4．（22-23八年级上·山东济宁·期中）如图，已知中，.在直线或上取一点P，使得是等腰三角形，则符合条件的P点有 个.
5．（22-23八年级上·陕西西安·阶段练习）如图，在平面直角坐标系中，已知点A（0，3），B（4，0），试在x轴上找点P使△ABP为等腰三角形，求点P的坐标．
6．（22-23八年级上·浙江金华·阶段练习）（1）如图1，线段OA的一个端点O在直线l上，且与直线l所成的锐角为50°，以OA为一边画等腰三角形，并且使另一个顶点P在直线l上，这样的等腰三角形能画 个．
（2）如图1，如果OA与直线l所成的锐角为60°，以OA为一边画等腰三角形，并且使另一个顶点P在直线l上，这样的等腰三角形能画 个．
想一想：如图2，△ABC中，∠A＝20°，∠B＝50°，过顶点C作一条直线，分割出一个等腰三角形这样的直线最多可以画 条．
算一算：如图3，在△ABC中，∠BAC＝20°，若存在过点C的一条直线，能把该三角形分成两个等腰三角形，试求∠B的度数．
【典型例题九 作等腰三角形(尺规作园)】
1．（22-23八年级上·河南周口·期末）“已知等腰三角形的底边和底边上的高，用尺规作图求作等腰三角形”里用到的基本作图是
A．作一条线段等于已知线段，作已知线段的垂直平分线B．作已知角的平分线
C．过直线外一点作已知直线的垂线D．作一个角等于已知角
2．（2023·河北保定·一模）如图，给出线段，，作等腰，使，边上的高.嘉嘉的作法是：①作线段；②作线段的垂线；③以点为圆心，为半径作弧，与分别交于点，；④连接，，为所求作的等腰三角形.上述作法的四个步骤中，你认为有错误的一步是（ ）
A．①B．②C．③D．④
3．（2023九年级·北京·专题练习）“直角”在初中几何学习中无处不在．课堂上李老师提出一个问题：如图1，已知．判断是否为直角（仅限用直尺和圆规）．小丽的方法如图2，在、上分别取点，，以点为圆心，长为半径画弧，交的反向延长线于点．若，则．李老师说小丽的作法正确，请你写出她作图的依据： ．
4．（22-23八年级上·福建宁德·期中）已知A（2，0），B（0，2），在x轴上确定点M，使三角形MAB是等腰三角形，则M点的坐标为 （任写一个）．
5．（23-24八年级上·陕西西安·期末）如图，已知线段，求作等腰三角形，使底边AB的长为，底上高的长为（不写作法，保留作图痕迹）．
6．（23-24七年级上·湖北襄阳·期末）如图．已知一个含有角的直角三角形，请利用它用两种不同的方法构造一个含角的直角三角形．（尺规作图，不写做法，保留作图轨迹）
【典型例题十 等腰三角形的性质和判定】
1．（23-24八年级下·吉林白山·阶段练习）如图，在平面直角坐标系中，的顶点，，，且，则点C关于y轴对称的点的坐标是（ ）
A．B．C．D．
2．（2024·浙江嘉兴·三模）在中， ， 小豪作图过程如下∶
（1） 以A为圆心， 长为半径作弧交于点 D，连结∶
（2）分别以C，D为圆心，大于 作弧交于点 E：
（3） 作射线 交 于点 F．
则下列结论正确的是（ ）
A．B．
C．D．
3．（23-24八年级上·广东湛江·期中）如图，在中，，，平分的外角，则 ．
4．（23-24八年级下·陕西渭南·期中）如图，，，点在线段的垂直平分线上且点，，三点共线，连接，若，，则线段的长度为 ．
5．（2024·陕西咸阳·模拟预测）如图，已知，．请用尺规作图法在的延长线上找一点D，连接，使得．（不写作法，保留作图痕迹）．
6．（23-24八年级下·山西太原·期中）如图，中，，点D是边延长线上一点．
(1)尺规作图：过点D作于点E，交于点F（要求：保留作图痕迹，标明字母，不写作法；如果完成有困难，可画出草图后解答（2）题）；
(2)在（1）得到的图中，求证：．
【典型例题十一 等腰三角形的定义】
1．（22-23七年级下·重庆渝中·期末）等腰三角形的一边长为，另一边长为，则它的周长为（ ）
A．B．C．D．或
2．（23-24八年级下·河北保定·期中）等腰三角形一边上的高与一腰所夹的锐角是，则该等腰三角形顶角是（ ）
（1）甲的结果是；（2）乙的结果是；（3）丙的结果是．
A．甲、乙的结果合起来才对B．乙、丙的结果合起来才对
C．甲、乙、丙的结果合起来才对D．甲、乙、丙的结果合起来也不对
3．（23-24七年级下·江西九江·期末）等腰三角形的一边等于1，一边等于3，则它的周长等于 ．
4．（23-24七年级下·重庆·阶段练习）已知等腰三角形的周长为18，其中一边长为5，则该等腰三角形的底边长为 ．
5．（2024七年级下·全国·专题练习）已知一个等腰三角形的周长为．
(1)如果腰长是底边的2倍，那么各边的长是多少？
(2)如果一腰上的中线将该等腰三角形的周长分为两部分，那么各边的长为多少？
6．（23-24八年级下·广东惠州·期中）如图，等腰的周长为，底边，的垂直平分线交于点，交于点，求的周长．
【典型例题十二 等边三角形的判定和性质】
1．（2024七年级下·全国·专题练习）在中，，则的周长是（ ）
A．2B．4C．6D．7
2．（2024七年级下·全国·专题练习）如图，已知的大小为，是内部的一个定点，且，点、分别是、上的动点，则周长的最小值等于（ ）
A．B．C．2D．1
3．（23-24七年级下·全国·假期作业）如图，在等边三角形中，点是边的中点，则 ．
4．（23-24七年级下·上海·阶段练习）在中，，要使是等边三角形需添加一个条件，这个条件可以是 ．（只需写出一种情况）
5．（23-24八年级上·甘肃庆阳·期中）如图，在中，，点在边上，连接．若，求证：是等边三角形．
6．（23-24八年级下·四川达州·期中）如图，为等边三角形，平分交于点D，交于点E．
(1)求证：是等边三角形．
(2)求证：．
【典型例题十三 含30度角的直角三角形】
1．（23-24八年级下·广西桂林·期中）如图，在中，，，的平分线交于，于点，若，则（ ）
A．B．C．D．
2．（23-24八年级下·陕西西安·期中）如图是某公园一段索道的示意图，已知A、B分别为索道的起点和终点，且A、B两点间的距离为40米，，则缆车从A点到B点的过程（的长）为（ ）
A．20米B．17.5米C．15米D．12.5米
3．（23-24八年级下·陕西宝鸡·期中）如图，是等边三角形，是延长线上一点，于点，交于点于点．若，，则的长为 ．
4．（2024七年级下·全国·专题练习）如图，在中，．分别以点A和C为圆心，以大于的长度为半径作弧，两弧相交于点P和点Q，作直线分别交，于点D和点E．若，则的长为 ．
5．（23-24八年级上·全国·课后作业）“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境，已知，，，这种草皮每平方米的售价是元，求购买这种草皮需要多少元．

6．（23-24八年级上·辽宁大连·期中）如图，是边长为的等边三角形，，点Q为射线边上一点，当的长为多少时，是直角三角形.

【变式训练1 等边对等角】
1．（23-24八年级上·黑龙江哈尔滨·阶段练习）等腰三角形底角为，则此等腰三角形的顶角度数为（ ）
A．B．C．或D．
2．（22-23八年级上·云南昭通·期中）等腰三角形有一个内角为，则它的顶角为（ ）
A．B．C．或D．不能确定
3．（22-23八年级上·江苏南京·期末）若等腰三角形的底角为55°，则这个等腰三角形的顶角是 °．
4．（22-23八年级上·云南昭通·期中）等腰三角形一个角的度数为，则顶角的度数为 ．
5．（2023八年级上·全国·专题练习）在等腰三角形中，有一个角为40°，求其余各角．
6．（23-24八年级下·陕西西安·期中）如图，在中，，求的度数．

【变式训练2 根据等边对等角证明】
1．（22-23八年级上·北京·期中）已知：是等腰三角形，，是底边上的高，下面结论不一定成立的是（ ）

A．B．C．平分D．
2．（2020·河北石家庄·模拟预测）老师在投影屏上展示了如下一道试题：
已知：如图，平分，．求证：．
证明：∵平分，∴（①角平分线定义），
∵，∴（②等角对等边），
∴③，
∴（④内错角相等，两直线平行）．
则以上证明过程中，结论或者依据错误的是一项是（ ）．
A．①B．②C．③D．④
3．（22-23八年级上·重庆江北·期末）如图，在中，，点都在边上，，若，则的长为 ．
4．（22-23八年级上·安徽·单元测试）如图，在中，，点在延长线上，于点，交于点，若，，则的长度为 .
5．（2023·北京丰台·一模）如图，△ABC中，AB=AC，D、E分别是BC、AC上的点，∠BAD与∠CDE满足什么条件时AD=AE？写出你的推理过程．
6．（23-24八年级上·江苏泰州·期中）已知：如图，在中，，点D在上，且．

(1)求证：；
(2)若，求∠C的度数．
【变式训练3 根据三线合一证明】
1．（22-23八年级下·四川泸州·期末）如图，在中，，是的平分线，若，则等于（ ）
A．3B．4C．5D．6
2．（22-23八年级上·吉林白城·阶段练习）如图．在中，．若是的角平分线，则下列说法错误的是（ ）
A．
B．
C．
D．
3．（23-24八年级上·浙江温州·阶段练习）如图，等腰中，，是的平分线，，则的长为 ．

4．（22-23八年级上·山东滨州·期末）如图，中，，，，、分别是、上的动点，则的最小值为 ．
5．（23-24八年级上·湖南益阳·期中）如图，中，，是边上的高，的周长为，，求的长．
6．（23-24八年级上·湖南岳阳·期中）如图，在中，点在延长线上，且是的中线，平分，交于点．

求证：
(1)；
(2)．
【变式训练4 格点图中画等腰三角形】
1．（22-23八年级上·吉林长春·期末）如图，在的正方形网格中，点A、B均在格点上．要在格点上确定一点C，连接和，使是等腰三角形，则网格中满足条件的点C的个数是（ ）
A．5个B．6个C．7个D．8个
2．（22-23七年级下·山东淄博·期末）如图所示的正方形网格中，网格线的交点称为格点．已知A，B是两个格点，如果点C也是图形中的格点，且△ABC为等腰三角形，所有符合条件的点C有（ ）
A．3个B．4个
C．5个D．6个
3．（22-23八年级上·湖北武汉·期中）在平面直角坐标系中，A（4，0），B（0，4），D在第一象限，且DO=DB，△DOA为等腰三角形，则∠OBD的度数为 ．
4．（22-23九年级上·江苏泰州·阶段练习）如图，A．B两点在正方形网格的格点上，每个方格都是边长为1的正方形、点C也在格点上，且△ABC为等腰三角形，则符合条件的点C共有 个．
5．（23-24八年级上·吉林长春·期末）图①、图②、图③均是的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，线段的端点均在格点上．只用无刻度的直尺，在图①、图②、图③中以为边各画一个等腰三角形，使其依次为锐角三角形、直角三角形、钝角三角形，且所画三角形的顶点均在格点上．

6．（22-23八年级上·吉林长春·期末）图①、图②、图③均是的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点，分别在三幅图中的线段上画出格点P，使点P满足以下要求：
(1)在图①中，连结，使最小；
(2)在图②中，连结、，使；
(3)在图③中，连结、，使为直角三角形．
【变式训练5 根据等角对等边证明等腰三角形】
1．（22-23八年级上·浙江金华·阶段练习）下列能断定△ABC为等腰三角形的是（ ）
A．∠A＝30°，∠B＝60°B．∠A+∠B＝∠C
C．∠A＝55°，∠B＝70°D．∠A：∠B＝1：2
2．（22-23八年级上·福建厦门·阶段练习）下列条件中，不能判定△ABC是等腰三角形的是( )
A．a=3，b=3，c=4B．a：b：c=4：5：6
C．∠B=50°，∠C=80°D．∠A：∠B：∠C =1：1：2
3．（22-23八年级上·浙江台州·期中） 如图，已知∠AOD＝28°，点C是射线OD上的一个动点，在点C的运动过程中，恰好是等腰三角形，则此时∠A所有可能的度数为 ．
4．（22-23八年级下·全国·课前预习）等有三角形的判定：如果一个三角形有 ，那么这两个角所对的边也相等（简写成“等角对等边”）．
几何书写：
∵
∴ AB＝AC （等角对等边）．
5．（22-23八年级上·江苏苏州·期末）如图，在△ABC中，AD平分∠BAC，点E在BA的延长线上，且EC∥AD．证明：△ACE是等腰三角形．
6．（22-23八年级上·四川德阳·阶段练习）如图，点是的平分线和的外角平分线的交点，，则线段、、之间有何数量关系，并证明.
【变式训练6 根据等角对等边证明边相等】
1．（22-23八年级上·广东佛山·阶段练习）在△ABC中，∠B=∠C，AB=5．则AC=（ ）
A．12B．9C．5D．2
2．（22-23八年级上·浙江嘉兴·期中）将一平板保护套展开放置在水平桌面上，其侧面示意图如图所示，若，，则的长为（ ）
A．B．C．D．
3．（22-23八年级上·湖南株洲·期中）如图所示，在中，，分别是和的平分线，且PD∥AB，PE∥AC，则的周长是 ．
4．（22-23七年级下·上海普陀·期中）如图，△ABC中，∠B，∠C的平分线相交于点F，过F作DE∥BC，分别交AB、AC于D、E，若AB+AC＝10，则△ADE的周长等于 ．
5．（23-24八年级上·福建泉州·阶段练习）如图，在中，．
(1)用尺规作的平分线，交于点D．（保留作图痕迹，不写作法）
(2)若，求证：．
6．（22-23八年级下·山东济南·期中）如图，在△ABC中，AE是∠BAC的角平分线，交BC于点E，DE∥AB交AC于点D．
(1)求证AD=ED；
(2)若AC=AB，DE=3，求AC的长．

【变式训练7 根据等角对等边求边长】
1．（23-24八年级上·湖南邵阳·期中）如图，在中，的垂直平分线交于点D，交于点E，，若，则的长是（ ）
A．2B．3C．4D．不能确定
2．（22-23八年级上·山西太原·阶段练习）在中，，，则的长为（ ）
A．1B．2C．3D．4
3．（22-23八年级上·吉林长春·期中）如图，在中，和的平分线交于点，过点作交 于，交 于，若，则的周长为 ．
4．（22-23七年级下·江苏盐城·期末）如图，∠ABC的平分线BF与△ABC中∠ACB的相邻外角∠ACG的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E，若BD＝7cm，DE＝3cm，求CE的长为 cm．
5．（22-23八年级·全国·课后作业）如图，在和中，为斜边，，、相交于点．
（1）请说明的理由；
（2）若，，求的长．
6．（22-23八年级上·福建福州·期中）如图，上午时，一条船从海岛出发，以海里小时的速度向正北方向航行，时到达海岛处．在海岛测得灯塔在北偏西的方向上，在海岛测得灯塔在南偏西的方向上，求海岛到灯塔的距离．
【变式训练8 直线上与已和两点组成等腰三角形的点】
1．（23-24八年级上·浙江宁波·期中）如图，在平面直角坐标系中，为坐标原点，四边形是矩形，顶点，，，的坐标分别为，，，，点在轴上，点在边上运动，使为等腰三角形，则满足条件的点有（ ）
A．3个B．4个C．5个D．6个
2．（22-23八年级上·北京房山·期末）如图，，点P为直线上的一个动点，若使得是等腰三角形．则符合条件的点P有（ ）
A．1个B．2个C．3个D．4个
3．（22-23八年级上·全国·期中）直线y＝x+3与坐标轴交于A、B两点，点C在坐标轴上，△ABC为等腰三角形，则满足条件的点C最多有 个．
4．（22-23八年级上·浙江杭州·开学考试）如图，B是直线l上的一点，线段与l的夹角为，点C在l上，若以为顶点的三角形是等腰三角形，则满足条件的点C共有 个．
【点睛】此题主要考查了等腰三角形的判定，利用分类讨论得出是解题关键．
5．（22-23七年级下·上海奉贤·期末）如图，在直线上有一点，直线外有一点，点在直线上，是以、为腰的等腰三角形．
（1）在图中画出
（2）已知，求
6．（22-23八年级上·山东潍坊·期中）如图，已知坐标系内点，在坐标轴上找一点A，使是等腰三角形（利用尺规作图，找到所有满足条件的情况，保留作图痕迹，并简单写出作图说明）．
【变式训练9 作等腰三角形(尺规作园)】
1．（22-23八年级上·广东广州·阶段练习）等腰但不等边的三角形的角平分线、高线、中线的总条数是（ ）
A．3B．5C．7D．9
2．（2023·湖北武汉·中考真题）如图，在Rt△ABC中，∠C=90°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为（ ）
A．4B．5C．6D．7
3．（22-23八年级上·江苏扬州·期末）△ABC中，以B为圆心，BC长为半径画弧，分别交AC、AB于D、E两点，并连接BD、DE，若∠A=30°，AB=AC，则∠BDE= ．
4．（22-23八年级上·河北秦皇岛·期中）已知△ABC的三边长分别为4、4、6，在△ABC所在平面内画一条直线，将△ABC分割成两个三角形，使其中的一个是等腰三角形，则这样的直线最多可画 条．
5．（22-23八年级下·陕西榆林·期末）如图，已知线段a，b，求作以3a为底边、以b为高的等腰三角形（不写作法，保留作图痕迹）

6．（22-23八年级上·湖北恩施·期中）（1）已知．请过点A作边上的高（保留作图痕迹，不写作法）；
（2）已知等腰三角形的底边长为a，底边上的高为h，求作这个等腰三角形（保留作图痕迹，不写作法）．
【变式训练10 等腰三角形的性质和判定】
1．（2024七年级下·全国·专题练习）如图，中，，且，垂直平分，交于点F，交于点E，若周长为16，，则为（ ）
A．5B．8C．9D．10
2．（23-24七年级下·陕西西安·阶段练习）如图，已知的面积为24，，点为边上一点，过点分别作于，于，若，则长为（ ）
A．6B．2C．4D．8
3．（23-24八年级上·江苏镇江·阶段练习）已知等腰的周长是，，则 ．
4．（23-24八年级上·广西来宾·期中）如图，在中，，，于点，若，且的周长为，则的长为 ．
5．（23-24八年级下·福建宁德·期中）如图，已知在等腰三角形纸片中，．利用尺规按以下要求作图．（不写作法，保留作图痕迹．）
请从以下两个问题中任选一题作答．
A题：作出一条裁剪线，使得该等腰三角形纸片分成两个等腰三角形，并说明理由．
B题：作出两条裁剪线，使得该等腰三角形纸片分成三个等腰三角形，并说明理由．
6．（23-24八年级下·陕西·期中）如图，在中，，与的角平分线交于点O，过点O作，分别交于点M，N．
(1)证明：是等腰三角形；
(2)与相等吗？对你的结论说明理由．
【变式训练11 等腰三角形的定义】
1．（23-24七年级下·上海嘉定·期末）已知等腰三角形的周长为10，一边长为2，那么它的一条腰长是（ ）
A．2B．2或10C．4D．2或4
2．（23-24八年级上·河南南阳·阶段练习）已知等腰三角形的底边和腰的长分别为5和6，则这个等腰三角形的周长为（ ）
A．15B．16C．17D．18
3．（23-24八年级上·浙江丽水·期末）一个等腰三角形的周长是20，若其中一条边长为8，这个等腰三角形的腰长是 ．
4．（23-24八年级上·重庆渝北·期中）如图，在中，，，，点Q是边上的一个动点，点Q从点B开始沿方向运动，且速度为每秒，设出发的时间为t秒．当点Q在边CA上运动时，出发 秒后，是以为腰的等腰三角形．
5．（23-24七年级下·江苏盐城·阶段练习）已知，的三边长为4，7，x．
(1)求x的取值范围；
(2)当为等腰三角形时，求x的值．
6．（23-24八年级上·广东广州·期中）如图所示，已知，为的中线，，的周长为24，求的周长．
【变式训练12 等边三角形的判定和性质】
1．（2024八年级·全国·竞赛）点M是正六边形内任一点，正六边形面积为18，若，则（ ）．
A．6B．3C．18D．9
2．（23-24八年级上·江苏盐城·期末）如图，，以点O为圆心，适当长为半径画弧交两边于点A、B，再以点A为圆心，长为半径画弧，交弧于点C，作射线，则的度数为（ ）
A．B．C．D．
3．（2024·广西桂林·一模）如图，在等边中，，平分，点在的延长线上，且，则的长为 ．
4．（23-24八年级上·湖南常德·期中）如图，，是延长线上的一点，，动点从点出发沿以的速度移动，动点从点发沿以的速度移动，如果点、同时出发，用表示移动的时间，当 时，是等腰三角形.

5．（23-24八年级上·福建南平·阶段练习）如图，点E在上，和都是等边三角形．求证：
(1)
(2)猜想：三条线段之间的关系是________，并说明理由．
6．（23-24八年级上·山东临沂·期末）已知，在中，，E是上一点，垂足为D，交于点F．若，试判断的形状，并说明理由．
【变式训练13 含30度角的直角三角形】
1．（2024·江苏盐城·一模）如图，在中，，的平分线交于D，于点E，若，则的长度为（ ）
A．B．C．D．
2．（23-24八年级上·安徽淮南·期末）如图，在中，，，点在边上，且，若，则的长为（ ）
A．2B．2.5C．3D．4
3．（23-24九年级下·黑龙江哈尔滨·阶段练习）在中，，点在直线上，过点作直线，垂足为点，若，则线段的长为 ．
4．（2024·辽宁沈阳·模拟预测）图1是一个地铁站人口的双翼闸机．如图2，它的双翼展开时，双翼边缘的端点A与B之间的距离为12cm，双翼的边缘，且与闸机侧立面夹角．当双翼收起时，可以通过闸机的物体的最大宽度为 ．
5．（22-23八年级下·广东深圳·期中）如图，在中，，D是上的一点，过点D作于点E，延长和，交于点F．
(1)求证：是等腰三角形；
(2)若，，，求的长．
6．（2023·重庆渝北·一模）在学习了特殊角的三角函数后，同学们熟练掌握了，，的三角函数值，老师又提出一个问题：中，，如何用所学知识求的正切值？聪明的小周很快有了思路：利用作垂直平分线构造等腰三角形，得到角与特殊角角的关系，从而解决问题，请根据她的思路完成下面的作图与填空如图．
解：用直尺和圆规作的垂直平分线交于点，交于点，连接（只保留作图痕迹）
垂直平分
①
中
②
中
③
④
1．（23-24八年级上·北京东城·期末）如图，在中，，D是的中点，在的延长线上取点E，连接，若，，则为（ ）．
A．B．C．D．
2．（2023·山东淄博·二模）如图，，点E在上，B，F，C，D四点在同一条直线上．若，则下列结论正确的是（ ）

A．B．
C．D．
3．（22-23七年级下·陕西西安·期末）如图，在Rt△ABC中，∠C=90°，∠A=20°，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的等腰三角形的个数最多为( )
A．4个B．5个C．6个D．7个
4．（23-24八年级上·辽宁鞍山·期中）如图，用圆规以直角顶点O为圆心，以适当长为半径画一条弧交两直角边于A，B两点，若再以A为圆心，以长为半径画弧，与前弧交于点C，作射线，则度数是（ ）
A．B．C．D．
5．（2024·云南昭通·一模）如图所示，在中，，，是斜边上的高，，那么等于（ ）
A．5B．6C．8D．12
6．（22-23八年级上·黑龙江哈尔滨·期中）如图，在中，，，的周长为150，则 ．
7．（22-23八年级上·江苏淮安·期中）如图，，是延长线上一点，若，动点从点出发沿以的速度移动，动点从点沿以的速度移动，如果点、同时出发，用表示移动的时间，当 时，是等腰三角形？
8．（23-24八年级上·山东日照·期中）如图，已知，在边上顺次取点，，，在边上顺次取点，使得，得到等腰，若得到的最后一个等腰三角形就是，则的度数的取值范围是 ．
9．（22-23八年级上·湖北荆门·期中）如图，在等边中，于D，点P、Q分别为、上的两个定点，且，，在上有一动点E使最短，则的最小值为 ．

10．（23-24八年级上·福建福州·期末）如图，在中，，，,，则的长为 ．
11．（22-23七年级下·山东济南·期中）如图，DC是AB的垂直平分线，交AB于点C，∠A=40°，求∠B的度数．
12．（23-24八年级上·江西赣州·期末）如图1，图2都是的正方形网格，每个小正方形的顶点称为格点．如图，线段的两端点均在格点上，在给定的网格中，按下列要求用无刻度的直尺画等腰，使点在格点上．
(1)在图1中，画以为腰的三角形；
(2)在图2中，画以为底的三角形．
13．（23-24八年级上·江苏泰州·阶段练习）如图，，，求证：直线垂直平分线．
14．（22-23八年级上·黑龙江哈尔滨·开学考试）下面为的网格，每个小正方形的边长为1，请按要求画图．要求：所画图形的顶点均在网格的格点上．
（1）在图1中画一个面积为6的锐角三角形；
（2）在图2中画一个面积为5，且有一个内角为45°的三角形．
15．（23-24八年级上·内蒙古通辽·期末）如图，在等腰中，，腰的垂直平分线交底于点，垂足为点．

(1)求的度数；
(2)若，求的长．
图形
等腰三角形
等边三角形
性 质
两条边都相等
三条边都相等
两个角都相等
三个角都相等，且都是60º
底边上的中线、高和顶角的平分线互相重合
每一边上的中线、高和这一边所对的角的平分线互相重合
对称轴（1条）
对称轴（3条）
图形
等腰三角形
等边三角形
判定
从边看：两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
从角看：两个角相等的三角形是等腰三角形
三个角都相等的三角形是等边三角形
等边三角形的判定方法：有一个角是60°的等腰三角形是等边三角形