人教A版普通高中数学一轮复习第9章第4节列联表与独立性检验课件

这是一份人教A版普通高中数学一轮复习第9章第4节列联表与独立性检验课件，共28页。PPT课件主要包含了是否独立，列联表与χ2的计算，反思感悟，独立性检验的综合应用等内容，欢迎下载使用。

·考试要求·1.通过实例，理解2×2列联表的统计意义．2．通过实例，了解独立性检验及其应用．
知识点　列联表与独立性检验1．判断下列说法的正误，正确的打“√”，错误的打“×”．(1)2×2列联表中的数据是两个分类变量的频数．(　　)(2)分类变量A和B的独立性检验无关，即两个分类变量互不影响．(　　)(3)χ2的大小是判断事件A和B是否相关的统计量．(　　)(4)在2×2列联表中，若|ad－bc|越小，则说明两个分类变量之间关系越强．(　　)
必备知识 落实“四基”
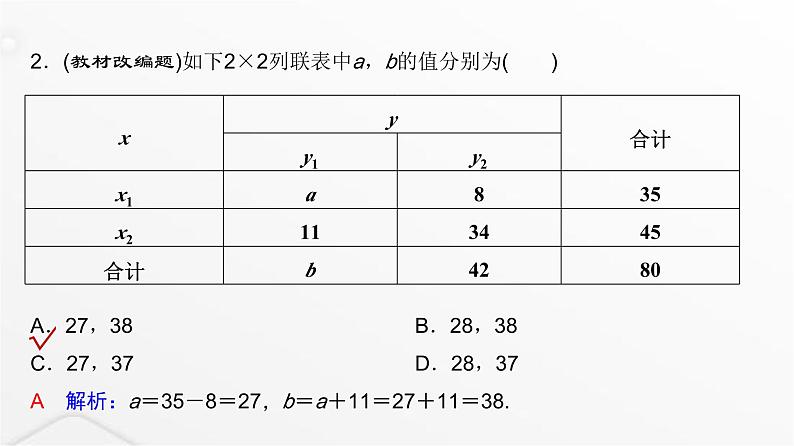
2．(教材改编题)如下2×2列联表中a，b的值分别为(　　)A．27，38B．28，38C．27，37D．28，37A　解析：a＝35－8＝27，b＝a＋11＝27＋11＝38.
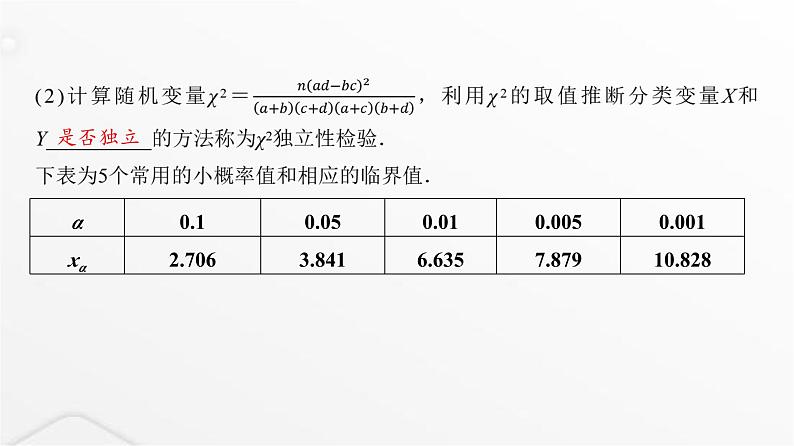
3．已知P(χ2≥6.635)＝0.01，P(χ2≥10.828)＝0.001.在检验喜欢某项体育运动与性别是否有关的过程中，某研究员搜集数据并计算得到χ2＝7.235，则根据小概率值α＝__________的χ2独立性检验，推断喜欢该项体育运动与性别有关．0．01　解析：因为6.635<7.235<10.828，所以由检验规则可知，根据小概率值α＝0.01的χ2独立性检验，推断喜欢该项体育运动与性别有关．
1．分类变量为了表述方便，我们经常会使用一种特殊的随机变量，以区别不同的现象或性质，这类随机变量称为分类变量．分类变量的取值可以用实数表示．
2．列联表与独立性检验(1)关于分类变量X和Y的抽样数据的2×2列联表：
3.应用独立性检验解决实际问题的几个步骤(1)提出零假设H0：X和Y相互独立，并给出在问题中的解释．(2)根据抽样数据整理出2×2列联表，计算χ2的值，并与临界值xα比较．(3)根据检验规则得出推断结论．(4)在X和Y不独立的情况下，根据需要通过比较相应的频率，分析X和Y间的影响规律．
1．为了研究某地动物受核辐射后对身体健康的影响，专家随机选取了110只羊进行了检测，并将有关数据整理为2×2列联表．　　　单位：只
核心考点 提升“四能”
则A，B，C，D的值依次为(　　)A．20，80，30，50B．20，50，80，30C．20，50，80，110D．20，80，110，50B　解析：30＋A＝50，所以A＝20，B＋10＝60，所以B＝50，所以C＝30＋B＝30＋50＝80，D＝A＋10＝20＋10＝30.
2．两个分类变量X和Y，其2×2列联表如表所示，对同一样本，以下数据能说明X与Y有关联的可能性最大的一组为(　　) A．m＝3B．m＝4C．m＝5D．m＝6
关于列联表及χ2的计算(1)2×2列联表在计算数据时要准确无误，关键是对涉及的变量分清类别．(2)计算χ2时遵循先化简后计算的原则，充分的约分可以简化数据的运算．
【例1】某公司为了拓展业务，对该公司某款手机的潜在客户进行调查，随机抽取国内外潜在用户代表各100名，调查用户对是否使用该手机的态度，得到如图所示的等高堆积条形图．由等高堆积条形图得到的数据，根据小概率值α＝0.005的χ2独立性检验，能否认为持乐观态度和国内外差异有关？
利用函数的图象刻画实际问题
解：由题意得2×2列联表如下：　　　　　　　　　　　　　单位：名
甲、乙两城市之间的长途客车均由A和B两家公司运营．为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城市之间的500个班次的长途客车准点情况，得到下面列联表：　　　　　　　　　　　　　 　单位：个
根据小概率值α＝0.1的独立性检验，能否认为甲、乙两城市之间的长途客车是否准点与客车所属公司有关？解：列联表如下：　　　　　　　　　　　　单位：个
【例2】某人工智能公司想要了解其开发的语言模型准确率的达标(准确率不低于80%则认为达标)情况与使用的训练数据集大小是否有关联，该公司随机选取了大型数据集和小型数据集各50个，并记录了使用这些数据集训练的语言模型在测试数据集上的准确率，根据小型数据集的准确率数据绘制成如图所示的频率分布直方图(各组区间分别为[50，60)，[60，70)，[70，80)，[80，90)，[90，100])．
(1)求a的值，并完成下面的2×2列联表；　　　　　　　　　　　　　单位：个
(2)根据小概率值α＝0.005的独立性检验，能否认为语言模型准确率是否达标与使用的训练数据集大小有关联？解：(1)由10×(0.010＋0.025＋a＋0.020＋0.010)＝1，解得a＝0.035.准确率不低于80%的小型数据集有50×(0.2＋0.1)＝15(个)，由此可得2×2列联表如下：　　　　　　　　　　　　　　单位：个
关于独立性检验的综合应用独立性检验的考查，往往与概率和抽样统计图等一起考查，这类问题的求解可以按各小题及提问的顺序，一步步进行下去，是比较容易解答的．单纯考查独立性检验往往用小题的形式，而且χ2的公式一般会在原题中给出．
以”智联世界，生成未来”为主题的2023世界人工智能大会在中国上海举行，人工智能的发展为许多领域带来了巨大的便利，但同时也伴随着一些潜在的安全隐患．为了调查不同年龄阶段的人对人工智能所持的态度，某机构从所在地区随机调查了100人，所得结果统计如下：
完成下列2×2列联表，并判断是否有99%的把握认为所持态度与年龄有关．　　　　　　　　　　　　　　　　　单位：人