沪教版八年级数学下册期中期末满分冲刺卷特训06期中选填题(上海精选归纳65题，20.1-22.2)(原卷版+解析)

这是一份沪教版八年级数学下册期中期末满分冲刺卷特训06期中选填题(上海精选归纳65题，20.1-22.2)(原卷版+解析)，共46页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。

1．（2023春·上海·八年级专题练习）以下函数中，属于一次函数的是（ ）
A．y＝B．y＝
C．y＝c（c为常数）D．y＝kx+b（k、b为常数）
2．（2022秋·上海静安·八年级新中初级中学校考期末）如果一次函数的图象经过原点，则的值为（ ）
A．0或1B．1C．0D．不存在
3．（2021·上海·九年级专题练习）若函数是一次函数，则m的值为（ ）
A．B．1C．D．2
4．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）已知函数，当时，的值为（ ）
A．6B．3C．D．
5．（2023春·八年级单元测试）已知一次函数的图象与直线平行，且过点，那么一次函数的表达式是（ ）
A．B．C．D．
6．（2023春·八年级单元测试）在一次函数中，y随x的增大而减小，那么常数m的取值范围是（ ）
A．；B．；C．；D．．
7．（2023春·上海宝山·八年级校考阶段练习）已知一次函数，那么下列结论正确的是（ ）
A．图像必经过点B．图像经过第一．二．三象限
C．当时，D．的值随的值增大而增大
8．（2022秋·上海青浦·八年级校考期末）在直角坐标平面内，一次函数的图像如图所示，那么下列说法正确的是（ ）
A．当时，B．方程 的解是
C．当时，D．不等式 的解集是
9．（2022春·上海普陀·九年级校考期中）已知直线ykxb经过第一、三、四象限，那么直线ybxk一定不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
10．（2023春·八年级单元测试）将一次函数与的图像画在同一坐标系中，正确的是（ ）
A．B．
C．D．
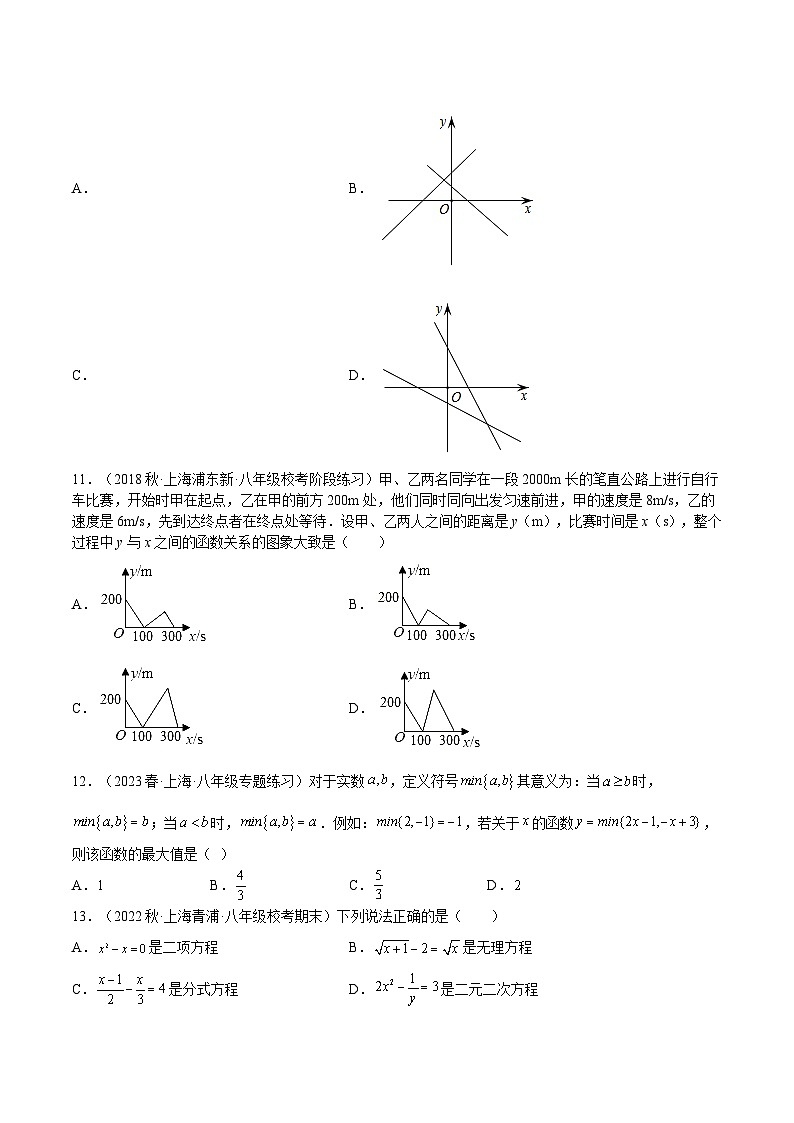
11．（2018秋·上海浦东新·八年级校考阶段练习）甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛，开始时甲在起点，乙在甲的前方200m处，他们同时同向出发匀速前进，甲的速度是8m/s，乙的速度是6m/s，先到达终点者在终点处等待．设甲、乙两人之间的距离是y（m），比赛时间是x（s），整个过程中y与x之间的函数关系的图象大致是（ ）
A．B．
C．D．
12．（2023春·上海·八年级专题练习）对于实数，定义符号其意义为：当时，；当时，．例如：，若关于的函数，则该函数的最大值是（ ）
A．B．C．D．
13．（2022秋·上海青浦·八年级校考期末）下列说法正确的是（ ）
A．是二项方程B．是无理方程
C．是分式方程D．是二元二次方程
14．（2022春·上海·八年级专题练习）若关于x的分式方程无解，则k的值为（ ）
A．B．－1C．1D．
15．（2022·上海·上海市娄山中学校考二模）下列方程中，有实数根的方程是（ ）
A．B．
C．D．
16．（2022春·上海浦东新·八年级校考期中）小明在解方程组的过程中，以下说法错误的是（ ）
A．可得，再用代入消元法解
B．令，，可用换元法将原方程组化为关于、的二元一次方程组
C．由得，再代入，可得一个关于的分式方程，亦可求解
D．经检验：是方程组的一组解
17．（2023春·八年级单元测试）用换元法解分式方程，如果设，那么原方程化为关于的整式方程是（ ）
A．B．
C．D．
18．（2022春·上海·八年级校考阶段练习）下列方程组中是二元二次方程组的是（ ）
A．B．C．D．
19．（2020春·八年级校考课时练习）张老师和李老师同时从学校出发，步行15千米去书店购买书籍，张老师比李老师每小时多走1千米，结果比李老师早到半小时，两位老师每小时各走多少千米？设李老师每小时走x千米，根据题意，所列的方程是（ ）
A．B．
C．D．
20．（2022春·上海·八年级专题练习）方程组的所有整数解的组数是（ ）
A．2B．3C．4D．5
21．（2022春·上海普陀·八年级校考期中）一个凸多边形的内角中最多有几个锐角( )
A．个B．个C．个D．个
22．（2023春·上海·八年级专题练习）如果一个多边形的内角和是其外角和的两倍，那么这个多边形是（ ）
A．六边形B．五边形C．四边形D．三角形
23．（2023春·上海·八年级专题练习）一个多边形边数每增加1条时，其内角和（ ）
A．增加B．增加C．不变D．不能确定
24．（2022春·上海嘉定·八年级校考期中）下列命题中不正确的是（ ）
A．两组对角分别相等的四边形是平行四边形
B．两组对边分别相等的四边形是平行四边形
C．一组对边平行且相等的四边形是平行四边形
D．对角线相等的四边形是平行四边形
25．（2022春·上海·八年级校考期中）已知四边形ABCD，有以下四个条件：①；②；③；④．从这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法种数共有（ ）
A．6种B．5种C．4种D．3种
26．（2022春·上海奉贤·八年级校考期中）如图平行四边形的对角线与相交于点，，，周长为16，那么对角线的长等于（ ）
A．4B．5C．6D．8
27．（2023春·上海·八年级专题练习）平面直角坐标系中，平行四边形三个顶点坐标分别为，则顶点B的坐标为（ ）
A．B．C．D．
28．（2021春·上海徐汇·八年级上海市民办华育中学校考期中）如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1，S2，S3，S4，则一定成立的是（ ）
A．S1+S2＞S3+S4B．S1+S2=S3+S4C．S1+S2＜S3+S4D．S1+S3=S2+S4
二、填空题
29．（2022春·上海·九年级上海市西南模范中学校考阶段练习）如果直线y＝ax＋b经过点（1，3），那么a＋b＝______．
30．（2023春·上海·八年级专题练习）已知函数是关于x的一次函数，则______．
31．（2022春·上海·八年级专题练习）以下函数中y是x的一次函数的有_________个．
①；②；③；④；⑤；⑥．
32．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）若一次函数中随的增大而减小，则的取值范围是______．
33．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）直线可以由直线沿着轴向______（填“上”“下”）平移______个单位得到．
34．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）直线与轴、y轴分别交于点A、B两点，则原点到直线的距离为___________．
35．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）若关于的一次函数的截距为1，则的值为___________．
36．（2023春·上海宝山·八年级校考阶段练习）如果直线经过点，那么不等式的解集为_________．
37．（2023春·上海宝山·八年级校考阶段练习）直线关于轴对称的直线的解析式为______．
38．（2023春·上海宝山·八年级校考阶段练习）函数的图象与轴．轴围成的三角形面积为______．
39．（2023春·上海·八年级专题练习）如图，在平面直角坐标系中，直线与坐标轴交于，两点，于点，是线段上的一个动点，连接，将线段绕点逆时针旋转，得到线段，连接，则线段的最小值为______．
40．（2023春·上海·八年级专题练习）、两地相距50千米，小张骑自行车从地到地，车速为13千米/小时，骑了小时后，小张离地千米，那么关于的函数解析式是___．
41．（2022秋·上海·八年级专题练习）上海磁悬浮列车在一次运行中速度V（千米/小时）关于时间t（分钟）的函数图象如图，回答下列问题．
（1）列车共运行了___分钟
（2）列车开动后，第3分钟的速度是___千米/小时．
（3）列车的速度从0千米/小时加速到300千米/小时，共用了___分钟．
（4）列车从___分钟开始减速．
42．（2023春·上海长宁·八年级上海市延安初级中学校考阶段练习）写出一个由一个二元一次方程和一个二元二次方程组成的方程组，使它的解是；，那么该方程组可以是__________．
43．（2023春·上海长宁·八年级上海市延安初级中学校考阶段练习）已知关于x的方程有增根，那么__________．
44．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）用换元法解分式方程时，如果设，那么可将原方程变形后表示为关于y的一元二次方程一般形式：___________．
45．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）无理方程：在实数范围内___________．（填写“有解”或“无解”）
46．（2023春·上海宝山·八年级校考阶段练习）若方程：有解，则的取值范围是______．
47．（2022秋·上海静安·八年级新中初级中学校考期末）写出一个由二元一次方程和一个二元二次方程组成的二元二次方程组___________，使它的解是和．
48．（2023春·八年级单元测试）方程组的解只有一组，则的取值范围是______．
49．（2022春·上海·九年级校考期中）方程的解是____________．
50．（2022春·上海浦东新·八年级校考期中）方程的根是______．
51．（2023春·八年级单元测试）如果方程无实数解，那么的取值范围是______．
52．（2022春·上海·八年级校考期中）某工人要完成个零件，起初机器出现故障，每分钟比原计划少加工个零件，加工个零件后，换了一台新机器，每分钟比原计划多加工个零件．已知用新机器加工零件的时间比前面用旧机器加工零件的时间少分钟，设原计划每分钟加工个零件，则可列方程为：______．
53．（2022春·上海·八年级专题练习）某次列车平均提速vkm/h．用相同的时间，列车提速前行驶skm．提速后比提速前多行驶50km．设提速前列车的平均速度是xkm/h．根据题意分别列出下列四个方程：①；②；③；④．则其中正确的方程有_________．
54．（2022秋·上海虹口·八年级上外附中校考阶段练习）小明在解方程时采用了下面的方法：由
，
又有，可得，将这两式相加可得，
将两边平方可解得，经检验是原方程的解．
请你学习小明的方法，解决下列问题：
（1）已知，则的值为___________．
（2）解方程，得方程的解为___________．
55．（2022秋·上海嘉定·九年级统考阶段练习）如果某个多边形的内角和为1260°，那么它的边数是 _____．
56．（2022秋·上海静安·八年级新中初级中学校考期末）如果一个多边形的内角和为，那么过这个多边形的一个顶点可作___________条对角线．
57．（2019春·上海·八年级上海市娄山中学校考阶段练习）在平行四边形中，的平分线把分成长度是3，4的两部分，则平行四边形的周长是_____．
58．（2023秋·上海青浦·八年级校考期末）如图，平行四边形中，，垂足分别是E、F，，则平行四边形的周长为_______．
59．（2023秋·上海青浦·八年级校考期末）如图所示，在平行四边形中，cm，cm，的平分线交于点，交的延长线于点，则___cm．
60．（2023春·上海·八年级专题练习）若一个平行四边形的一个内角平分线把一条边分成和两条线段，则该平行四边形的周长为__________．
61．（2022春·上海·八年级校考期中）如图，在平行四边形中，于点，于点，，且，则平行四边形的周长为______．
62．（2021春·上海·八年级上海市进才中学北校校考期中）如图，中，，于，交于，若，则的大小是________．
63．（2021春·上海杨浦·八年级校考期中）如图，在平行四边形中，对角线的垂直平分线交于点，连接．若平行四边形的周长为20cm，则的周长为______cm．
64．（2022春·上海杨浦·八年级校考期末）如图， 的对角线与相交于点，将翻折使点与点重合，点落在点，已知（是锐角），那么的度数为______．（用的代数式表示）
65．（2023春·上海·八年级专题练习）在平行四边形中，和交于点O，，，如果将沿直线翻折后，点B落在点E处，那么的面积等于________．
特训06 期中选填题（上海精选归纳65题，20.1-22.2）
一、单选题
1．（2023春·上海·八年级专题练习）以下函数中，属于一次函数的是（ ）
A．y＝B．y＝
C．y＝c（c为常数）D．y＝kx+b（k、b为常数）
【答案】A
【分析】根据一次函数的概念：形如（均是常数），对四个选项逐一进行判断即可．
【解析】A、中，，是一次函数，故该选项符合题意；
B、是反比例函数，故该选项不符合题意；
C、（c是常数）是常函数，故该选项不符合题意；
D、当时，就不是一次函数，故该选项不符合题意；
故选：A．
【点睛】此题考查一次函数的概念，熟练掌握一次函数的概念是解此题的关键．
2．（2022秋·上海静安·八年级新中初级中学校考期末）如果一次函数的图象经过原点，则的值为（ ）
A．0或1B．1C．0D．不存在
【答案】B
【分析】将原点坐标代入，得到关于m的一元二次方程，再根据一次项系数不能为0为方根的解进行取舍即可．
【解析】解：将原点坐标代入，
可得，
解得，，
是一次函数，
，
，
故选B．
【点睛】本题考查一次函数的图象和性质，以及解一元二次方程，解题的关键是注意解析式中一次项的系数不能为0．
3．（2021·上海·九年级专题练习）若函数是一次函数，则m的值为（ ）
A．B．1C．D．2
【答案】C
【分析】根据一次函数的定义列式计算即可得解．
【解析】解：根据题意得，且，
解得且，
所以，．
故选：C．
【点睛】本题主要考查了一次函数的定义，一次函数的定义条件是：、为常数，，自变量次数为1．
4．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）已知函数，当时，的值为（ ）
A．6B．3C．D．
【答案】C
【分析】由题意得：函数，令，得到，整理得，两边同时平方，最后解一元二次方程即可求出的值，但最后将求出的值代入检验．
【解析】已知函数，
当时，
∴，
∴，
∴，
∴，
∴，
∴，
∴，，
经检验：时不符合题意，故舍去，
∴当时，的值为，
故选：C
【点睛】本题主要考查已知函数值，求自变量的值，解一元二次方程，熟练掌握相关知识点是解题的关键．
5．（2023春·八年级单元测试）已知一次函数的图象与直线平行，且过点，那么一次函数的表达式是（ ）
A．B．C．D．
【答案】B
【分析】根据两直线平行，结合题意即可设一次函数解析式为，再利用待定系数法求解即可．
【解析】解：∵一次函数的图象与直线平行，
∴可设一次函数解析式为：．
将点代入，得：，
解得：，
∴一次函数的表达式为：．
故选B．
【点睛】考查了一次函数图象平行的问题．解题关键是明确一次函数图象平行时k的值不变，再利用待定系数法求解析式．
6．（2023春·八年级单元测试）在一次函数中，y随x的增大而减小，那么常数m的取值范围是（ ）
A．；B．；C．；D．．
【答案】D
【分析】先根据一次函数的增减性得出关于的不等式，求出的取值范围即可．
【解析】解：∵在一次函数中，随的增大而减小，
∴，解得．
故选：D．
【点睛】本题主要考查了一次函数的性质．一次函数，当时，随的增大而减小；当时，随的增大而增大．
7．（2023春·上海宝山·八年级校考阶段练习）已知一次函数，那么下列结论正确的是（ ）
A．图像必经过点B．图像经过第一．二．三象限
C．当时，D．的值随的值增大而增大
【答案】C
【分析】根据一次函数的图像上点的特征对选项A进行判断；根据一次函数的性质对选项B、D进行判断；利用时，函数图像的特征对选项C进行判断；即可得出答案．
【解析】解：A、当时，，则点不在函数图像上，故此选项不符合题意；
B、，
此函数的图像经过第一、二、四象限，故此选项不符合题意；
C、∵函数与轴的交点横坐标是，函数函数值随的增大而减小，
∴交点的右边，
即：当时，，故此选项符合题意；
D、，
y随x的增大而减小，故此选项不符合题意；
故选：C．
【点睛】此题考查了一次函数的图像与性质，熟练掌握一次函数的图像与性质、学会用数形结合的思想方法是解此题的关键．
8．（2022秋·上海青浦·八年级校考期末）在直角坐标平面内，一次函数的图像如图所示，那么下列说法正确的是（ ）
A．当时，B．方程 的解是
C．当时，D．不等式 的解集是
【答案】C
【分析】根据函数的图象直接进行解答即可．
【解析】解：由函数的图象可知，
当时，，A选项错误，不符合题意；
方程 的解是，B选项错误，不符合题意；
当时，，故C正确，符合题意；
不等式 的解集是，故D错误，不符合题意．
故选：C．
【点睛】本题考查的是一次函数的图象，利用数形结合求解是解答此题的关键．
9．（2022春·上海普陀·九年级校考期中）已知直线ykxb经过第一、三、四象限，那么直线ybxk一定不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【答案】C
【分析】根据直线y=kx+b经过第一，三，四象限，可以判断k、b的正负，根据一次函数图象的性质，从而可以判断直线y=bx+k经过哪几个象限，不经过哪个象限．
【解析】解：∵直线y=kx+b经过第一，三，四象限，
∴k>0，b<0，
∴直线y=bx+k经过第一、二、四象限，不经过第三象限，
故选：C．
【点睛】本题考查一次函数的性质，明确题意，熟练掌握并灵活运用一次函数的性质是解题的关键．
10．（2023春·八年级单元测试）将一次函数与的图像画在同一坐标系中，正确的是（ ）
A．B．
C．D．
【答案】C
【分析】根据一次函数的图像与系数的关系依次分析各项即可．
【解析】解：一次函数的与一次函数的矛盾，错误；
从图像知，一次函数的图像不经过原点，错误；
一次函数的与一次函数的一致，正确；
从图像知，一次函数的图像不经过原点，错误．
故选：．
【点睛】本题主要考查一次函数的图像，掌握一次函数的图像是解决问题的关键．
11．（2018秋·上海浦东新·八年级校考阶段练习）甲、乙两名同学在一段2000m长的笔直公路上进行自行车比赛，开始时甲在起点，乙在甲的前方200m处，他们同时同向出发匀速前进，甲的速度是8m/s，乙的速度是6m/s，先到达终点者在终点处等待．设甲、乙两人之间的距离是y（m），比赛时间是x（s），整个过程中y与x之间的函数关系的图象大致是（ ）
A．B．
C．D．
【答案】C
【分析】先算出甲到达终点的时间，由此算出二者之间的最大距离，再算出乙到达终点的时间，由此找出点的坐标，结合点的坐标利用待定系数法求出函数解析式，根据函数解析式分析四个选项即可得出结论．
【解析】解：当甲骑到终点时所用的时间为：2000÷8＝250（s），
此时甲乙间的距离为：2000﹣200﹣6×250＝300（m），
乙到达终点时所用的时间为：（2000﹣200）÷6＝300（s），
∴最高点坐标为（250，300）．
甲追上乙时，所用时间为（s）
当0≤x≤100时，设y关于x的函数解析式为y＝k1x+b1，
有
解得：
此时y＝﹣2x+200；
当100＜x≤250时，设y关于x的函数解析式为y＝k2x+b2，
有
解得：
此时y＝2x﹣200；
当250＜x≤300时，设y关于x的函数解析式为y＝k3x+b3，
有
解得：
此时y＝-6x+1800．
∴整个过程中y与x之间的函数图象是C．
故选：C．
【点睛】此题考查了一次函数的应用，解题的关键是理解题意，找到题中的关键点，利用待定系数法求得每段函数解析式．
12．（2023春·上海·八年级专题练习）对于实数，定义符号其意义为：当时，；当时，．例如：，若关于的函数，则该函数的最大值是（ ）
A．B．C．D．
【答案】C
【分析】根据定义先列不等式：和，确定其，对应的函数，画图象可知其最大值．
【解析】解：由题意得：，解得：，
当时，，
当时，，，
由图象可知：此时该函数的最大值为；
当时，，
当时，，，
由图象可知：此时该函数的最大值为；
综上所述，，的最大值是当所对应的的值，
如图所示，当时，，
故选：C
【点睛】本题考查了新定义、一元一次不等式及一次函数的交点问题，认真阅读理解其意义，并利用数形结合的思想解决函数的最值问题．
13．（2022秋·上海青浦·八年级校考期末）下列说法正确的是（ ）
A．是二项方程B．是无理方程
C．是分式方程D．是二元二次方程
【答案】B
【分析】利用无理方程及二项方程以及高次方程的定义进行判断即可得到答案；
【解析】解：是一元二次方程，不是二项方程，故A不符合题意；
是无理方程，故B符合题意；
是一元一次方程，故C不符合题意；
是分式方程，故D不符合题意；
故选B．
【点睛】本题考查了无理方程及二项方程的定义，解题的关键是熟悉这些方程的定义．
14．（2022春·上海·八年级专题练习）若关于x的分式方程无解，则k的值为（ ）
A．B．－1C．1D．
【答案】D
【分析】先令分母为零求增根，在把分式方程化为整式方程，最后把增根代入整式方程即可求出答案．
【解析】解： 分式方程无解

解得
原方程化为：



把 代入得

解得
故选：D．
【点睛】本题考查分式方程的增根，掌握增根产生的原因并求出增根，把分式方程转化为整式方程是解题的关键．
15．（2022·上海·上海市娄山中学校考二模）下列方程中，有实数根的方程是（ ）
A．B．
C．D．
【答案】B
【分析】根据一元二次方程根的判别式、解分式方程、无理方程的方法与步骤逐项判断即可．
【解析】解：A、一元二次方程的判别式，故方程无实数根，故A不符合题意；
B、分式方程去分母得，解得，经检验是原方程的解，故选项B符合题意；
C、要使根式有意义，则且，即，此时，故C不符合题意；
D、，故无实数解，故D不符合题意；
故选B．
【点睛】此题主要考查了一元二次方程、分式方程、无理方程的解的情况，熟练掌握一元二次方程、分式方程与无理方程的解法是解此题的关键．
16．（2022春·上海浦东新·八年级校考期中）小明在解方程组的过程中，以下说法错误的是（ ）
A．可得，再用代入消元法解
B．令，，可用换元法将原方程组化为关于、的二元一次方程组
C．由得，再代入，可得一个关于的分式方程，亦可求解
D．经检验：是方程组的一组解
【答案】B
【分析】②①得出，整理后得出，即可判断选项A；换元后得出方程组，即可判断选项B；由①求出，代入②后即可判断选项C；把代入方程组中的两个方程，看看方程的两边是否都相等，即可判断选项D．
【解析】解：，
A．②①，得，
整理得：，再用代入消元法解，故本选项不符合题意；
B．令，，则原方程组化为：
，
不能得出关于、的二元一次方程组，故本选项符合题意；
C．由①得，
把代入②得：
，得出一个关于的分式方程，即可求解，故本选项不符合题意；
D．把代入①，得
左边，右边，左边右边，
把代入②，得
左边，右边，左边右边，
所以是方程组的解，故本选项不符合题意；
故选：B．
【点睛】本题考查了解分式方程组和方程组的解，能把分式方程组转化成方程和理解方程组的解的定义是解此题的关键．
17．（2023春·八年级单元测试）用换元法解分式方程，如果设，那么原方程化为关于的整式方程是（ ）
A．B．
C．D．
【答案】A
【分析】由，原方程可化为，去分母把分式方程化成整式方程，即可得出答案．
【解析】解：设，
分式方程可化为，
化为整式方程：，
故选：A．
【点睛】本题考查了换元法解分式方程，掌握换元法及正确把分式方程化成整式方程是解决问题的关键．
18．（2022春·上海·八年级校考阶段练习）下列方程组中是二元二次方程组的是（ ）
A．B．C．D．
【答案】D
【分析】含有两个未知数，且未知数的最高次数是2，这样的整式方程组是二元二次方程组，根据定义逐一分析即可．
【解析】解：不符合整式方程组的条件，故A不符合题意；
不符合整式方程组的条件，故B不符合题意；
的最高次项的次数是1，故C不符合题意；
符合二元二次方程组的条件，故D符合题意；
故选D
【点睛】本题考查二元二次方程组的识别，掌握该定义是求解本题的关键．
19．（2020春·八年级校考课时练习）张老师和李老师同时从学校出发，步行15千米去书店购买书籍，张老师比李老师每小时多走1千米，结果比李老师早到半小时，两位老师每小时各走多少千米？设李老师每小时走x千米，根据题意，所列的方程是（ ）
A．B．
C．D．
【答案】B
【分析】根据等量关系“结果比李老师早到半小时”即可列出方程．
【解析】解：李老师所用时间为：，张老师所用的时间为：；
所列方程为：﹣＝．
故选：B．
【点睛】本题考查分式方程的应用，找出题目的等量关系是解题的关键．
20．（2022春·上海·八年级专题练习）方程组的所有整数解的组数是（ ）
A．2B．3C．4D．5
【答案】C
【分析】根据幂为1，可以判断底数为1，或指数为零，底数不为零，或底数为﹣1，指数为偶数三种情况，分三种情况讨论即可．
【解析】解：∵，
∴y＝1或 或，
①当y＝1时，
∵x+y＝1，
∴x＝0，
∴；
②当x2+3x+2＝0 时，
（x+2）（x+1）＝0，
解得x＝﹣2或x＝﹣1，
当x＝﹣2时，
﹣2+y＝1，
∴y＝3，
当x＝﹣1时，
﹣1+y＝1，
∴y＝2，
所以或；
③当y＝﹣1时，﹣1+x＝1，
∴x＝2，
此时 x2+3x+2＝4+6+2＝12，
∴符合题意，
综上所述所有整数解的组数为4，
故选：C．
【点睛】本题考查了方程组的整数解问题，关键是根据幂为1，判断出底数和指数的大小．
21．（2022春·上海普陀·八年级校考期中）一个凸多边形的内角中最多有几个锐角( )
A．个B．个C．个D．个
【答案】C
【分析】根据任意凸多边形的外角和是可知它的外角中，最多有个钝角，则内角中，最多有个锐角．
【解析】解：一个凸多边形的内角中，最多有个锐角．
理由是：因为凸多边形的外角和是度，在外角中最多有个钝角，如果超过个，则和一定大于度，多边形的内角与外角互为邻补角，
所以外角中最多有个钝角，内角中就最多有个锐角．
故选：C．
【点睛】本题考查多边形的内角和外角，注意每个内角与其相邻的外角是邻补角，由于多边形的外角和是不变的，所以要分析内角的情况可以借助外角来分析．
22．（2023春·上海·八年级专题练习）如果一个多边形的内角和是其外角和的两倍，那么这个多边形是（ ）
A．六边形B．五边形C．四边形D．三角形
【答案】A
【分析】多边形的外角和是，则内角和是．设这个多边形是n边形，内角和是，这样就得到一个关于n的方程，从而求出边数n的值．
【解析】解：设这个多边形是n边形，根据题意，得
，
解得：．
故这个多边形是六边形．
故选：A．
【点睛】本题考查了多边形的内角与外角，熟记内角和公式和外角和定理并列出方程是解题的关键．根据多边形的内角和定理，求边数的问题就可以转化为解方程的问题来解决．
23．（2023春·上海·八年级专题练习）一个多边形边数每增加1条时，其内角和（ ）
A．增加B．增加C．不变D．不能确定
【答案】A
【分析】根据多边形的内角和公式：（n-2）•180° 判断即可．
【解析】解：∵n边形的内角和=（n-2）×180°，
∴多边形的边数增加1，其内角和增加180°，
故选：A．
【点睛】本题考查多边形的内角和公式，理解多边形内角和公式是求解本题的关键．
24．（2022春·上海嘉定·八年级校考期中）下列命题中不正确的是（ ）
A．两组对角分别相等的四边形是平行四边形
B．两组对边分别相等的四边形是平行四边形
C．一组对边平行且相等的四边形是平行四边形
D．对角线相等的四边形是平行四边形
【答案】D
【分析】根据平行四边形的判定方法逐一进行判断即可．
【解析】解：A、两组对角分别相等的四边形是平行四边形，故选项正确，不符合题意；
B、两组对边分别相等的四边形是平行四边形，故选项正确，不符合题意；
C、一组对边平行且相等的四边形是平行四边形，故选项正确，不符合题意；
D、对角线互相平分的四边形是平行四边形，故选项错误，符合题意．
故选：D．
【点睛】本题主要考查平行四边形的判定方法，熟记平行四边形的判定方法是解题的关键．
25．（2022春·上海·八年级校考期中）已知四边形ABCD，有以下四个条件：①；②；③；④．从这四个条件中任选两个，能使四边形ABCD成为平行四边形的选法种数共有（ ）
A．6种B．5种C．4种D．3种
【答案】C
【分析】根据平行四边形的判定定理判断即可．
【解析】根据两组对边分别平行的四边形是平行四边形，可构成①③；
根据两组对边分别相等的四边形是平行四边形，可构成②④；
根据一组对边平行且相等的四边形是平行四边形，可构成①②或③④，
一共有4种组合，
故选C．
【点睛】本题考查了平行四边形的判定，熟练掌握判定定理是解题的关键．
26．（2022春·上海奉贤·八年级校考期中）如图平行四边形的对角线与相交于点，，，周长为16，那么对角线的长等于（ ）
A．4B．5C．6D．8
【答案】D
【分析】根据平行四边形的性质得出，，根据，得出，根据周长为16，得出，即可得出结果．
【解析】解：∵四边形ABCD为平行四边形，
∴，，
∵，
∴，
∵周长为16，
∴，
即，
∴，
∴，故D正确．
故选：D．
【点睛】本题主要考查了平行四边形的性质，熟练掌握平行四边形对角线互相平分，是解题的关键．
27．（2023春·上海·八年级专题练习）平面直角坐标系中，平行四边形三个顶点坐标分别为，则顶点B的坐标为（ ）
A．B．C．D．
【答案】A
【分析】由平行四边形的性质可得，，根据平移的性质可求得顶点B的坐标．
【解析】解：∵四边形是平行四边形，
∴，．
∵平行四边形三个顶点坐标分别为，，，
点向左平移2个单位，再向下平移3个单位得到点
∴向左平移2个单位，再向下平移3个单位得到点的坐标是，
∴点．
故选：A．
【点睛】本题考查了平行四边形的性质，平移的性质，掌握平移的性质是本题的关键．
28．（2021春·上海徐汇·八年级上海市民办华育中学校考期中）如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1，S2，S3，S4，则一定成立的是（ ）
A．S1+S2＞S3+S4B．S1+S2=S3+S4C．S1+S2＜S3+S4D．S1+S3=S2+S4
【答案】D
【分析】由平行四边形的性质得出S1+S3=平行四边形ABCD的面积，S2+S4=平行四边形ABCD的面积，即可得出结论．
【解析】∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，
∴S1+S3=平行四边形ABCD的面积，
S2+S4=平行四边形ABCD的面积，
∴S1+S3=S2+S4，
故选D．
【点睛】此题考查了平行四边形的性质以及三角形的面积问题．此题难度适中，注意掌握数形结合思想的应用．
二、填空题
29．（2022春·上海·九年级上海市西南模范中学校考阶段练习）如果直线y＝ax＋b经过点（1，3），那么a＋b＝______．
【答案】3
【分析】把点（1，3）代入，即可求解．
【解析】解：∵直线y＝ax＋b经过点（1，3），
∴a＋b＝3．
故答案为：3
【点睛】本题主要考查了一次函数的图象和性质，熟练掌握一次函数的图象和性质是解题的关键．
30．（2023春·上海·八年级专题练习）已知函数是关于x的一次函数，则______．
【答案】-2
【分析】根据一次函数与二次函数的定义求解．
【解析】解：根据题意得：且，
解得：m=-2．
故答案为：-2．
【点睛】本题主要考查了一次函数的定义，一次函数y=kx+b的定义条件是：k、b为常数，k≠0，自变量次数为1．
31．（2022春·上海·八年级专题练习）以下函数中y是x的一次函数的有_________个．
①；②；③；④；⑤；⑥．
【答案】4
【分析】根据一次函数的定义“一般地，形如（k，b是常数，k≠0）的函数，叫做一次函数”进行解答即可得．
【解析】解：①，不是一次函数；
②，是一次函数；
③，不是一次函数；
④，是一次函数；
⑤，是一次函数；
⑥，是一次函数；
综上，②④⑤⑥是一次函数，有4个一次函数，
故答案为：4．
【点睛】本题考查了一次函数的识别，解题的关键是熟记一次函数的定义．
32．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）若一次函数中随的增大而减小，则的取值范围是______．
【答案】##
【分析】在中，当时y随x的增大而增大，当时y随x的增大而减小．由此列不等式可求得k的取值范围．
【解析】解：∵一次函数中y随x的增大而减小，
∴，解得，
故答案为：．
【点睛】本题主要考查一次函数的增减性，掌握一次函数的增减性是解题的关键．
33．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）直线可以由直线沿着轴向______（填“上”“下”）平移______个单位得到．
【答案】 上 5
【分析】利用直线平移的规律求解．
【解析】解：直线可以由直线沿y轴向向上平移5个单位得到．
故答案为：上，5．
【点睛】本题考查了一次函数图象与几何变换：对于一次函数，把直线向上平移或向下平移个单位所得直线解析式为或．
34．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）直线与轴、y轴分别交于点A、B两点，则原点到直线的距离为___________．
【答案】
【分析】根据坐标轴上点的坐标特点，代入直线解析式求出点A，B的坐标，再由勾股定理求出，再由，即可求解．
【解析】解：如图，过点O作于点C，
当时，，解得：，
∴，
∴，
当时，，
∴，
∴，
∴，
∵，
∴，
解得：．
故答案为：．
【点睛】本题主要考查了一次函数与坐标轴的交点问题，勾股定理，熟练掌握一次函数的图象是解题的关键．
35．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）若关于的一次函数的截距为1，则的值为___________．
【答案】4
【分析】由题意得：关于的一次函数的截距为1，则一次函数的与轴交于，将代入函数解析式，得到，解方程，即可求得的值．
【解析】∵关于的一次函数的截距为1，
∴一次函数的与轴交于，
将将代入函数解析式，
∴，
∴，
故答案为：4
【点睛】本题主要考查一次函数的于坐标轴的交点问题，熟练掌握一次函数的图像性质是解题的关键．
36．（2023春·上海宝山·八年级校考阶段练习）如果直线经过点，那么不等式的解集为_________．
【答案】．
【分析】先画出函数图象，然后观察函数图象，比较函数图象的高低（即比较函数值的大小），确定对应的自变量的取值范围．
【解析】当时，，
∴函数图象还经过点．
如图，
∴当时，．
故答案为：．
【点睛】本题考查了一次函数与一元一次不等式，数形结合是解答本题的关键．
37．（2023春·上海宝山·八年级校考阶段练习）直线关于轴对称的直线的解析式为______．
【答案】
【分析】找到原直线解析式上的关于相应的坐标轴对称的点．
【解析】解：可从直线上找两点：这两个点关于y轴的对称点是，那么这两个点在直线关于y轴对称的直线上，
则
解得：．
∴．
故答案为：．
【点睛】本题考查了一次函数图象的几何变换，要注意轴对称的性质．
38．（2023春·上海宝山·八年级校考阶段练习）函数的图象与轴．轴围成的三角形面积为______．
【答案】6
【分析】根据函数与x轴的交点的纵坐标为0，把代入函数的表达式中，即可求出函数与x轴的交点坐标；根据函数与y轴交点的横坐标为0，把代入表达式中，即可求出函数与y轴的交点坐标；根据一次函数的图象与两坐标轴围成的图形是直角三角形，并结合直角三角形面积公式，问题很容易就能解答了．
【解析】解：∵当时，，解得，
∴函数图象与x轴的交点坐标为；
当时，，
∴函数图象与y轴的交点坐标为；
∴函数图象与两坐标轴围成的图形的面积为．
故答案为：6．
【点睛】本题考查的是一次函数图象上点的坐标特点，熟知坐标轴上点的坐标特点是解题的关键．
39．（2023春·上海·八年级专题练习）如图，在平面直角坐标系中，直线与坐标轴交于，两点，于点，是线段上的一个动点，连接，将线段绕点逆时针旋转，得到线段，连接，则线段的最小值为______．
【答案】
【分析】由点的运动确定的运动轨迹是在与轴垂直的一段线段，当线段与垂直时，线段的值最小．
【解析】解：由已知可得，
三角形是等腰直角三角形，
，
，
又是线段上动点，将线段绕点逆时针旋转，
在线段上运动，所以的运动轨迹也是线段，
当在点时和在点时分别确定的起点与终点，
的运动轨迹是在与轴垂直的一段线段，
当线段与垂直时，线段的值最小，

在中，，，
，
又是等腰直角三角形，
，
．
故答案为．
【点睛】此题考查了直角三角形的性质，一次函数图象上点的坐标特点，动点运动轨迹的判断，垂线段最短，熟练掌握一次函数图象的性质是解题的关键．
40．（2023春·上海·八年级专题练习）、两地相距50千米，小张骑自行车从地到地，车速为13千米/小时，骑了小时后，小张离地千米，那么关于的函数解析式是___．
【答案】
【分析】直接利用总路程行驶路程离地距离，进而得出关系式．
【解析】解：由题意可得：．
故答案为：．
【点睛】此题主要考查了函数关系式，正确理解题意得出等式是解题关键．
41．（2022秋·上海·八年级专题练习）上海磁悬浮列车在一次运行中速度V（千米/小时）关于时间t（分钟）的函数图象如图，回答下列问题．
（1）列车共运行了___分钟
（2）列车开动后，第3分钟的速度是___千米/小时．
（3）列车的速度从0千米/小时加速到300千米/小时，共用了___分钟．
（4）列车从___分钟开始减速．
【答案】 8 300 2 5
【分析】（1）根据函数图象的坐标，解答即可；
（2）根据函数图象的坐标，解答即可；
（3）根据函数图象的坐标，解答即可；
（4）根据函数图象的坐标，解答即可．
【解析】解：（1）列车共运行了8分钟；
故答案为：8；
（2）列车开动后，第3分钟的速度是300千米/小时；
故答案为：300；
（3）列车的速度从0千米/小时加速到300千米/小时，共用了2分钟；
故答案为：2；
（4）列车从5分钟开始减速．
故答案为：5．
【点睛】本题考查了函数图象，观察函数图象获得有效信息是解题关键．
42．（2023春·上海长宁·八年级上海市延安初级中学校考阶段练习）写出一个由一个二元一次方程和一个二元二次方程组成的方程组，使它的解是；，那么该方程组可以是__________．
【答案】
【分析】解答本题时，首先观察给出的两组解的特点，发现两组解中第一组中的与第二组中的互为相反数，第一组中的与第二组中的互为相反数，所以可以肯定的是无论哪组中的与的差都是，两组中的与的积都是，所以得到符合题意的一组方程组．
【解析】解：由题可得：
∵，，，，
∴，
故填：．
【点睛】本题考查了二元一次方程和一个二元二次方程，熟练掌握其定义是解此题的关键．
43．（2023春·上海长宁·八年级上海市延安初级中学校考阶段练习）已知关于x的方程有增根，那么__________．
【答案】
【分析】先去分母得，再把增根代入即可求得k值．
【解析】解：，
去分母得：，
由分式方程有增根，得到，即，
把代入整式方程，
解得．
把代入整式方程
无解．
故答案为：．
【点睛】本题主要考查分式方程的解法及增根问题，解题的关键是熟知分式方程的解法．
44．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）用换元法解分式方程时，如果设，那么可将原方程变形后表示为关于y的一元二次方程一般形式：___________．
【答案】
【分析】将原分式方程中的全部换成y，最后去分母化成整式方程即可．
【解析】解：化简得：
，
把代入得：，
两边同时乘以y得：，
故答案为：．
【点睛】本题考查了整体换元法、去分母将分式方程化为整式方程，正确代入以及去分母是解题关键．
45．（2023春·上海浦东新·八年级上海市进才中学北校校考阶段练习）无理方程：在实数范围内___________．（填写“有解”或“无解”）
【答案】无解
【分析】已知，则，两边同时平方，解方程，即可得出该方程在实数范围内无解．
【解析】∵，
∴，
∴，
∴，
当时，， 不符合题意，
∴是增根，应舍去，
∴无理方程：在实数范围无解，
故答案为：无解．
【点睛】本题主要考查无理方程的解法，熟练掌握无理方程的解法是解题的关键．
46．（2023春·上海宝山·八年级校考阶段练习）若方程：有解，则的取值范围是______．
【答案】
【分析】根据二次根式有意义的条件列出关于的不等式求解即可．
【解析】解：∵，即：，
∵，
∴，
解得：，
故答案为：．
【点睛】本题考查了无理方程，根据二次根式有意义的条件列出关于的不等式是解答本题的关键．
47．（2022秋·上海静安·八年级新中初级中学校考期末）写出一个由二元一次方程和一个二元二次方程组成的二元二次方程组___________，使它的解是和．
【答案】（答案不唯一）
【分析】根据方程组的解可得，再由平方差公式得到，则可写出满足条件的一个方程组为．
【解析】解：方程组的解为和，
，
，
方程组可以是，
故答案为：答案不唯一）．
【点睛】本题考查二元二次方程组，熟练掌握二元一次方程和二元一次方程的基本形式，根据所给的条件写出符合题意的方程组是解题的关键．
48．（2023春·八年级单元测试）方程组的解只有一组，则的取值范围是______．
【答案】
【分析】根据条件表示方程组的解，再求的范围．
【解析】解：，
由，得或，
，．
当时，代入得：，
原方程组的一组解为：，
当时，代入得：，
原方程只有一组解，
无解，
．
．
故答案为：．
【点睛】本题考查二元二次方程组的解，根据第一个方程，求得，是解题的关键．
49．（2022春·上海·九年级校考期中）方程的解是____________．
【答案】
【分析】方程移项后两边平方，化无理方程为整式方程，求解并检验即可．
【解析】解：移项，得，
两边平方，得，
整理，得，
所以．
经检验，是原方程的解．
故答案为：．
【点评】本题考查了无理方程，解题的关键是掌握解无理方程的一般步骤，同时注意验根．
50．（2022春·上海浦东新·八年级校考期中）方程的根是______．
【答案】或##或
【分析】将方程化为二项方程，因式分解法解方程即可求解．
【解析】解：，
即，
∴，
∵，
∴，
即，
，
或，
经检验，或，是原方程的解，
方程的根是或，
故答案为：或．
【点睛】本题考查了解二项方程，将方程因式分解是解题的关键．
51．（2023春·八年级单元测试）如果方程无实数解，那么的取值范围是______．
【答案】k<-1
【分析】移项后得出，根据算术平方根的非负性得出，求出此时，再求出的取值范围即可．
【解析】解：，
，
，
若方程无实数解，必须，
，
故答案为：．
【点睛】本题考查了解无理方程和解一元一次不等式，能根据算术平方根的非负性得出是解此题的关键．
52．（2022春·上海·八年级校考期中）某工人要完成个零件，起初机器出现故障，每分钟比原计划少加工个零件，加工个零件后，换了一台新机器，每分钟比原计划多加工个零件．已知用新机器加工零件的时间比前面用旧机器加工零件的时间少分钟，设原计划每分钟加工个零件，则可列方程为：______．
【答案】
【分析】根据题意可知：用新机器加工零件的时间比前面用旧机器加工零件的时间少分钟，即可列出相应的分式方程．
【解析】解：由题意可得：
，
故答案为：．
【点睛】本题考查由实际问题抽象出分式方程，解答本题的关键是明确题意，找出等量关系，列出相应的方程．
53．（2022春·上海·八年级专题练习）某次列车平均提速vkm/h．用相同的时间，列车提速前行驶skm．提速后比提速前多行驶50km．设提速前列车的平均速度是xkm/h．根据题意分别列出下列四个方程：①；②；③；④．则其中正确的方程有_________．
【答案】①③
【分析】设提速前列车平均速度是xkm/h，则提速后列车平均速度是（x+v）km/h，根据时间=路程÷速度及相同时间里面路程比等于速度比，即可得出关于x的分式方程，再对比四个选项后即可得出结论．
【解析】解：设提速前列车平均速度是xkm/h，则提速后列车平均速度是（x+v）km/h，
依题意得：①；③；④．
故其中正确的方程有①③．
故答案为：①③．
【点睛】本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．
54．（2022秋·上海虹口·八年级上外附中校考阶段练习）小明在解方程时采用了下面的方法：由
，
又有，可得，将这两式相加可得，
将两边平方可解得，经检验是原方程的解．
请你学习小明的方法，解决下列问题：
（1）已知，则的值为___________．
（2）解方程，得方程的解为___________．
【答案】
【分析】（1）根据题目所给方法，可求的值，然后结合，即可求出的值；
（2）根据题目所给方法，可求，再解方程即可．
【解析】解：（1），
又，
∴
∴；
（2）
，
又，
∴，
两式相加，得，
两边同时平方，得，
解得，
经检验，是原方程的解．
故答案为：；．
【点睛】本题考查了解无理方程，熟练掌握无理方程的解法，准确计算是解题的关键．
55．（2022秋·上海嘉定·九年级统考阶段练习）如果某个多边形的内角和为1260°，那么它的边数是 _____．
【答案】9
【分析】根据多边形的内角和公式列方程即可求解．
【解析】解：根据题意列方程，得
（n﹣2）•180°＝1260°，
解之，得n＝9．
故答案为：9．
【点睛】本题主要考查了多边形的内角和定理，求边数的问题就可以转化为解方程的问题来解决．
56．（2022秋·上海静安·八年级新中初级中学校考期末）如果一个多边形的内角和为，那么过这个多边形的一个顶点可作___________条对角线．
【答案】4
【分析】根据多边形的内角和是，可以求出多边形的边数，再根据多边形的一个顶点的对角线的条数与边数的关系：一个顶点的对角线条数等于边数减3，即可得解．
【解析】解：根据题意，得
，
解得：，
那么过这个多边形的一个顶点可作条对角线．
【点睛】本题考查根据多边形的内角和计算公式求多边形的边数，过多边形的一个顶点的对角线的条数边数．
57．（2019春·上海·八年级上海市娄山中学校考阶段练习）在平行四边形中，的平分线把分成长度是3，4的两部分，则平行四边形的周长是_____．
【答案】22或20##20或22
【分析】根据平分及可得出，从而根据的长可求出平行四边形的周长．
【解析】解：在平行四边形中，，则．
∵平分，
∴，
∴，
∴，
当时，
平行四边形的周长为：．
当时，
平行四边形的周长为：．
故答案为：22或20．
【点睛】本题考查平行四边形的性质、等腰三角形的判定；熟练掌握平行四边形的性质，证明是解答本题的关键．
58．（2023秋·上海青浦·八年级校考期末）如图，平行四边形中，，垂足分别是E、F，，则平行四边形的周长为_______．
【答案】20
【分析】由平行四边形的性质得，再证，然后由含角的直角三角形的性质得即可解答．
【解析】解：∵四边形是平行四边形，
∴，
∵，
∴，
∴，
∵，
∴，
∴
∵，
∴，
∴平行四边形的周长，
故答案为：20．
【点睛】本题主要考查了平行四边形的性质、含30°角的直角三角形的性质等知识点，熟练掌握平行四边形的性质是解题的关键．
59．（2023秋·上海青浦·八年级校考期末）如图所示，在平行四边形中，cm，cm，的平分线交于点，交的延长线于点，则___cm．
【答案】3
【分析】由平分得到，又由平行四边形两组对边分别平行可以推出，然后可以得到，从而求出．
【解析】解：平分，
，
，
，
，
，
cm，
故答案为：3．
【点睛】本题考查求线段长问题，涉及角平分线定义、平行四边形性质、等腰三角形的判定与性质等知识，熟练掌握等腰三角形的判定与性质是解决问题的关键．
60．（2023春·上海·八年级专题练习）若一个平行四边形的一个内角平分线把一条边分成和两条线段，则该平行四边形的周长为__________．
【答案】22cm或26cm
【分析】利用平行四边形的性质和角平分线证出∠BAE＝∠BEA，得出AB＝BE，由此求出另一边，从而求出周长，注意两种情况．
【解析】解：如图所示：
∵四边形ABCD是平行四边形，
∴AB＝CD，AD＝BC，，
∵∠A的平分线交BC于点E，
∴∠BAE＝∠DAE
∵，
∴∠DAE＝∠BEA，
∴∠BAE＝∠BEA，
∴AB＝BE，
分两种情况进行讨论：
当BE＝3cm，EC＝5cm时，AB＝BE＝3cm，BC＝BE+EC＝8cm，平行四边形的周长＝2×（3＋8）＝22（cm）；
当BE＝5cm，EC＝3cm时，AB＝BE＝5cm，BC＝BE+EC＝8cm，平行四边形的周长＝2×（5＋8）＝26（cm）；
综上所述：▱ABCD的周长是22或26cm．
故答案为：22cm或26cm．
【点睛】本题考查了平行四边形的性质、等腰三角形的判定；熟练掌握平行四边形的性质，证明AB＝BE是解题的关键．
61．（2022春·上海·八年级校考期中）如图，在平行四边形中，于点，于点，，且，则平行四边形的周长为______．
【答案】
【分析】要求平行四边形的周长就要先求出、的长，利用平行四边形的性质和勾股定理即可求出结果．
【解析】解：，
，
，
则，，
设，则，
在中，根据勾股定理可得，，
同理可得：，
则平行四边形的周长是，
故答案为：．
【点睛】本题考查了平行四边形的性质，解题关键是利用平行四边形的性质结合等腰直角三角形的性质、勾股定理来解决有关的计算和证明．
62．（2021春·上海·八年级上海市进才中学北校校考期中）如图，中，，于，交于，若，则的大小是________．
【答案】
【分析】由，可做辅助线，取的中点，连接，根据平行四边形的性质，可得是，由直角三角形斜边上的中线等于斜边的一半，可得是等腰三角形，进而可得，根据直角三角形的两锐角互余即可求得
【解析】取的中点，连接，
四边形是平行四边形
，
即
故答案为：
【点睛】本题考查了平行四边形的性质，等腰三角形的性质，添加辅助线是解题的关键．
63．（2021春·上海杨浦·八年级校考期中）如图，在平行四边形中，对角线的垂直平分线交于点，连接．若平行四边形的周长为20cm，则的周长为______cm．
【答案】10
【分析】根据平行四边形的对边相等及线段垂直平分线的性质，即可求得
【解析】解：∵的垂直平分线交于点，交于点，
∴，
∵平行四边形的周长为20cm，
∴，
∴，
∴的周长
．
故答案为：10．
【点睛】本题考查了平行四边形的性质，线段垂直平分线的性质，结合图形得到的周长是解决本题的关键．
64．（2022春·上海杨浦·八年级校考期末）如图， 的对角线与相交于点，将翻折使点与点重合，点落在点，已知（是锐角），那么的度数为______．（用的代数式表示）
【答案】##
【分析】先画出图形，由折叠的性质证明≌，继而可得是直角三角形，，根据，可求的度数．
【解析】解：如图所示：
由折叠的性质可得：，，
在和中，
，
≌（SAS），
，
，
，
．
故答案为：．
【点睛】本题考查了翻折变换的性质以及平行四边形的性质，解决问题的关键是掌握：翻折前后对应边相等、对应角相等，解题时注意：平行四边形的对角线互相平分．
65．（2023春·上海·八年级专题练习）在平行四边形中，和交于点O，，，如果将沿直线翻折后，点B落在点E处，那么的面积等于________．
【答案】
【分析】连接OE，过点O作OF⊥DE于点F．利用翻折的性质可得出△DOE为等边三角形，进而可得AC∥DE，故S△ADE＝S△DOE，直接求三角形DOE的面积即可得出答案．
【解析】解：连接OE，过点O作OF⊥DE于点F．
由翻折可知，∠AOB＝∠AOE＝60°，OB＝OD＝OE＝BD＝5，
∵∠DOE＝180°−∠AOB−∠AOE＝60°，
∴△DOE为等边三角形，
∴∠EDO＝∠AOB＝60°，EF＝DF，
∴AC∥DE，
∴S△ADE＝S△DOE，
∵，DE＝OD＝5，
∴S△ADE＝S△DOE＝．
故答案为：．
【点睛】本题考查翻折的性质、平行四边形的性质以及等边三角形的性质，解题的关键是准确作出辅助线，利用数形结合思想求解．