北京市怀柔区 2023-2024学年七年级下学期期末数学试题

这是一份北京市怀柔区 2023-2024学年七年级下学期期末数学试题，共13页。试卷主要包含了9的算术平方根是，不等式x-1>0的解是等内容，欢迎下载使用。

2024.7
一、选择题（本题共30分，每小题3分）
下列各题均有四个选项，其中只有一个是符合题意的．
1.9的算术平方根是
A. 81 B. 3 C. -3 D.
2.不等式x-1>0的解是
A. -1 B. 0 C. 1 D. 2
3.如果a＞b，那么下列不等式不成立的是
A.a+3>b+3 B. > C. a2>b2 D.-3a<-3b
4.若是关于x，y的二元一次方程的一个解，则a的值为
A. -2 B. 2 C. -4 D. 4
5.如图，直线a，b被c所截，下列四个结论：
①∠1和∠3互为对顶角； ②∠4和∠8是同位角；
③∠3和∠7是内错角； ④∠4和∠7是同旁内角.
其中，结论一定正确的有
A.4个 B.3个 C.2个 D. 1个
6.如图，直线AB与CD交于点O，OE⊥CD于点O，若∠COB=153°，则∠AOE的度数为
A. 43° B. 53° C. 63° D. 73°
7.小明一家在自驾游时，发现某高速路对行驶汽车的速度在正常情况下有如图规定.设小客车的速度为千米/小时，则在行车道①行驶速度v应满足的条件是
A.60≤v≤120 B. 60≤v≤90 C. 120≤v≤100 D. 100≤v≤120
8.下列调查活动，适合使用全面调查的是
A.调查某班同学体育选考科目 B.调查全市月人均用水量
C.调查某品牌蓄电池的使用寿命 D.调查某纪录片在线收视率
9. 在《算法统宗》里记载了一道趣题：
原文：九百九十九文钱，甜果苦果买一千，四文钱买苦果七，十一文钱九个甜，甜苦两果各几个?请君布算莫迟疑!
意思是：用九百九十九文钱共买了一千个甜果和苦果，其中四文钱可以买苦果七个，十一文钱可以买甜果九个，请问甜、苦果各买几个?
下列是四位同学的解答：
①小明：设苦果买x个, 甜果买y个,根据题意可列方程组为
②小刚：设苦果买x个, 甜果买y个,根据题意可列方程组为
③小勇：设苦果买x个, 甜果买(1000-x)个,根据题意可列方程为
④小强：设苦果买x个, 甜果买(1000-x)个,根据题意可列方程为
其中，以上解答一定正确的是
A.①②③ B.②③④ C.①③ D.②④
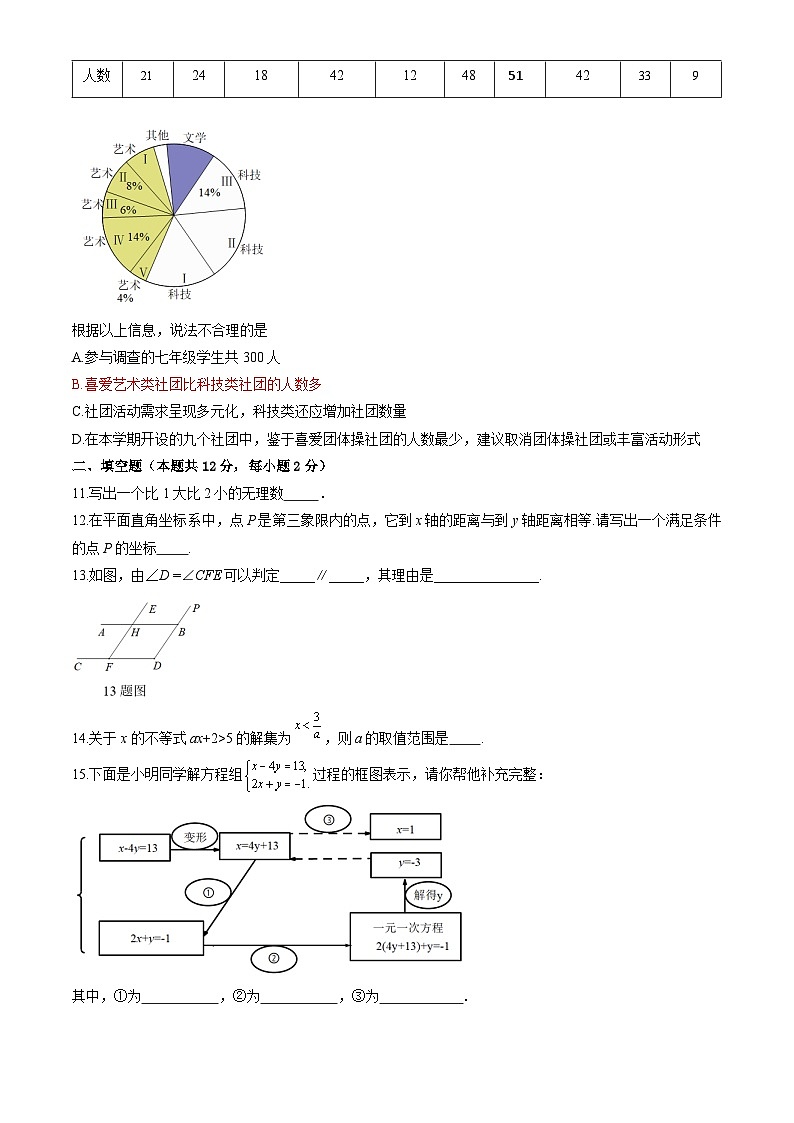
10.某初中校在本学期课后服务周三时间为学生开设社团活动，共开设艺术Ⅰ（剪纸社团）、
艺术Ⅱ（花艺社团）、艺术Ⅲ（戏曲社团）、艺术Ⅳ（足篮排社团）、艺术Ⅴ（团体操社团）、科技Ⅰ（机器人社团）、科技Ⅱ（航模社团）、科技Ⅲ（爱猫社团）、文学（话剧表演社团）等九个社团,七年级的学生全部参与.为下学期更好的开设学生喜欢的社团活动，学校组织七年级“我最喜爱的一个社团”调查活动，将调查结果绘制成如图所示的统计图表（不完整）.
根据以上信息，说法不合理的是
A.参与调查的七年级学生共300人
B.喜爱艺术类社团比科技类社团的人数多
C.社团活动需求呈现多元化，科技类还应增加社团数量
D.在本学期开设的九个社团中，鉴于喜爱团体操社团的人数最少，建议取消团体操社团或丰富活动形式
二、填空题（本题共12分，每小题2分）
11.写出一个比1大比2小的无理数 ．
12.在平面直角坐标系中，点P是第三象限内的点，它到x轴的距离与到y轴距离相等.请写出一个满足条件的点P的坐标 .
13.如图，由∠D =∠CFE可以判定_____∥_____，其理由是_______________.
14.关于x 的不等式ax+2>5的解集为，则a的取值范围是 .
15.下面是小明同学解方程组过程的框图表示，请你帮他补充完整：
其中，①为 ，②为 ，③为 .
16.如图，在平面直角坐标系xOy中，已知点M(1，-4)，N(4，-2)，将线段MN平移，得到线段PQ（点M的对应点为点P，点N的对应点为点Q），线段MN上任一点（x，y）在平移后的对应点为（x+a，y+b），其中a≥0，b≥0.
(1)若点P与点N恰好重合，则a=_________，b=_________；
(2)若a+b=5，且平移后三角形NPQ的面积最大，则此时a=_________，b=_________.
三、解答题（本题共58分，其中，第17-19小题，每小题4分，第20-27小题，每小题5分，第28小题6分）
17.计算：
18.解方程组：
19.解方程组：
20.下面是小明同学求不等式 -(3-x)≥1解集并在数轴上表示解集的解答过程：
第一步：(3x+2)-(3-x)≥1；
第二步：×3x+×2 -×3 ≥1；
第三步：6x+ -9+3x ≥4；
第四步：6x+3x≥9+4-4；
第五步：9x≥9；
第六步：x≥1.
(1)请将第二、三步和在数轴上表示解集补充完整；

(2)第二步变形的依据是 ；
(3)第三步变形的目的是 .
21.已知不等式2x+3≤x+5与1-3(x-1)<6-x同时成立，求x的整数值.
22.如图，在平面直角坐标系中，三角形ABC的三个顶点分别是A(-3，0)，B(-4，-2)，C(0，-3)，请你解答下列问题：
(1)在平面直角坐标系中画出三角形ABC；
(2)将三角形ABC先向右平移5个单位，再向上平移3个单位.画出平移后的三角形A1B1C1.
(3)把(2)中三角形A1B1C1各个顶点的横坐标保持不变，纵坐标增加3，得到三角形A2B2C2.直接写出三角形A2B2C2的面积.
23.如图，点O在直线l外，点A在直线上，连接OA. 选择适当的工具作图.
(1)在直线上作点B，使得OB⊥l于点B；
(2)连接OB；
(3)在直线上取一点C(不与A，B重合)，连接OC；
(4)在OA，OB，OC中，线段 最短，依据是 .
24. 小明在学校组织的社会调查活动中负责了解所居住的社区880户居民的家庭年使用管道天然气气量情况，他随机调查了80户居民的家庭年使用管道天然气气量(单位：立方米，简称：年用气量).对数据x（年用气量）进行整理、描述和分析.注：年用气量取整数.
a.绘制了被抽取的80户居民的家庭年用气量频数分布表和频数分布直方图.
家庭年用气量的频数分布表
家庭年用气量的频数分布直方图
b.家庭年用气量在279.5≤x＜369.5这一组的是：
280 280 285 290 290 298 298 300 300
301 301 301 305 317 322 323 356 362
根据以上信息，完成下列问题：
(1)将两个统计表(图)补充完整；
北京市居民用管道天然气价格表
(2)下表是北京市居民用管道天然气销售价格表，请你估计小明所居住的社区多少户家庭年用气量按第一档缴费即可.
25.完成下面的证明:
如图，AB∥CD, ∠1=∠2，∠3=∠4；
求证：AC∥BD
证明：∵∠1=∠2，（已知）
∴∠ 1+∠CBP=∠2+∠ ① ，（等式性质1）
即 ∠ABC =∠ ② .
∵AB∥CD，（已知）
∴∠ ③ =∠ABC.（ 两直线平行，内错角相等 ）
∵∠3=∠4 ,（已知）
∴∠3=∠ ④ ,（ 等量代换 ）
∴ ⑤ .（同位角相等，两直线平行）
26.我们知道方程组的解与方程组中每个方程的系数和常数项有联系，系数和常数项经过一系列变形、运算就可以求出方程组的解.因此，在现代数学的高等代数学科将系数和常数项排成一个表的形式，规定：关于x，y的二元一次方程组可以写成矩阵的形式.例如：可以写成矩阵的形式.
(1)填空：将写成矩阵形式为：；
(2)若矩阵所对应的方程组的解为求a与b的值.
27.三角形ABC中，∠ACB平分线CM与AB相交于点M，MN⊥AC，垂足为点N.
(1)如图1，三角形ABC是直角三角形，∠ACB=90º.
①补全图1；
②直接写出∠CMN的度数；
(2)如图2，三角形ABC是锐角三角形.过点N作NP∥BC，交AB于点P.用等式表示∠PNM，∠NMC与∠ACB三者之间的数量关系并说明理由.
(3)三角形ABC是钝角三角形，其中90º <∠ACB<180º. 过点N作NP∥BC，交AB于点P，
直接写出∠PNM，∠NMC与∠ACB三者之间的数量关系.
28.对于平面直角坐标系xOy中的图形Q和图形Q上的任意点P(x，y)，给出如下定义：
将点P(x，y)平移到P '(x+a，y+a)称为将点P进行“a(a是实数)型直角平移”，点P '称为将点P进行“a型直角平移”的对应点；将图形Q上的所有点进行“a型直角平移”称为将图形Q进行“a型直角平移”．
例如：将点P(-3，1)平移到P '(-2，2)，则点P '称为将点P进行“1型直角平移”的对应点；将点P(x，y)平移到P '(x-π，y-π)，则点P '称为将点P进行“-π型直角平移”的对应点.
已知点A(-3，-2)和点B(-7，-2).
将点A(-3，-2)进行“2型直角平移”后的对应点A '的坐标为___________；
(2)将线段AB进行“-2型直角平移”后得到线段A 'B '，点K1(-5，-4)，K2(-10，-4)，K3(-8.7，-4) 中，在线段M 'N '上的点是_________________；
(3)若线段AB进行“a型直角平移”后与坐标轴有公共点，则a的取值是______________；
(4)已知点E(-2，-5)，F(3，0),点H是线段EF上的一个动点，将点A进行“a型直角平移”后得到的对应点为A '.画图、观察、归纳可得，当a的取值范围是________ _____时， HA '的最小值保持不变.
参考答案
选择题（本题共30分，每小题3分）
下列各题均有四个选项，其中只有一个是符合题意的．
二、填空题（本题共12分，每小题2分）
11.答案不唯一，如：，π-2等. 12.答案不唯一.横纵坐标相等，且均为负值即可.
13.EF，PD，同位角相等，两直线平行. 14. a<0.
15.代入，消去x，解得x. 16.(1)3，2；(2)0，5.
三、解答题（本题共58分，其中，第17-19小题，每小题4分，第20-27小题，每小题5分，第28小题6分）
17. 计算：
解：原式=4+(-3)-3+
=-2.………………………………………………………………………………4分
①
②
解方程组：
解：
①代入②，得：3(5-2y)+4y=13，
15-6y+4y=13,
y=1.
将y=1代入①，得x=5-2×1，
解得：x=3.
所以这个方程组的解是…………………………………………………………………4分
19.解方程组：
①②
解：
由①变形得：2x-3y=9. ③
③×2，得：4x-6y=18. ④
②-④，得：15y=-15,
y=-1.
将 y=-1代入①，2x=9+3×(-1),
2x=6，
x=3.
所以这个方程组的解是………………………………………………………………4分
20.
(1)；4；
…………………………………………………………………………………………………3分
(2)去括号法则；…………………………………………………………………………………4分
(3)去分母. ………………………………………………………………………………………5分
21.
解：
解不等式①，得x≤2. ……………………………………………………………1分
解不等式②，得x>-1. ……………………………………………………………3分
所以不等式组的解集为-1 所以整数x的值是0，1，2. ………………………………………………………5分
22.
(1)(2)如图；
……………………………………………4分
(3). …………………………………………………………………………………………5分
23.
(1)(2)(3)如图；
…………………………………………3分
(4)OB；垂线段最短. …………………………………………………………………………5分
24. (1)
…………………………………………………………………………………………………3分
(2)880×=748(户)
所以估计小明所居住的社区748户家庭年用气量按第一档缴费即可.
…………………………………………………………………………………………………5分
25.①CBP，②PBD，③4，④PBD，⑤AC∥BD.
…………………………………………………………………………………………………5分
26.
(1)…………………………………………………………………………………2分
(2)矩阵所对应的关于x，y的二元一次方程组为………………3分
此方程组的解为
将代入方程组得：…………………………………………4分
由①得a=-2.由②得b=1.
所以a，b的值分别是-2和1.…………………………………………………………………5分
(1)①补全图1；
…………………………………………1分
②45º ；…………………………………………………………………………………………2分
(2)∠PNM，∠NMC与∠ACB之间的数量关系为∠NMC=∠PNM+∠ACB.
理由如下：
过点M作MQ//BC，交AC于点Q.
∴∠QMC=∠BCM.
∵PN//BC，
∴MQ//PN.
∴∠PNM=∠NMQ.
∴∠NMC=∠NMQ+∠QMC=∠PNM+∠BCM.
∵BM平分∠ACB，
∴∠BCM =∠ACB .
∴∠NMC=∠PNM+∠ACB. ………………………………………………………………4分
(3)∠NMC=∠ACB-∠PNM. …………………………………………………………… 5分
28.
(1) (-1，0)； …………………………………………………………………………………1分
(2)K1，K3；………………………………………………………………………………………3分
(3)a= 2或3≤a≤7. ……………………………………………………………………………5分
(4)-1≤a≤4. ……………………………………………………………………………………6分
考生须知
1.本试卷共8页，共三道大题，28道小题，满分100分。考试时间90分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上，在试卷上作答无效。
4.在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。
5.考试结束，将本试卷、答题卡一并交回。
社团
艺术Ⅰ
艺术Ⅱ
艺术Ⅲ
艺术Ⅳ
艺术Ⅴ
科技Ⅰ
科技Ⅱ
科技Ⅲ
文学
其他
人数
21
24
18
42
12
48
51
42
33
9
年用气量分组
(立方米)
划记
频数
9.5≤x＜99.5

4
99.5≤x＜189.5
12
189.5≤x＜279.5

279.5≤x＜369.5
18
369.5≤x＜459.5

6
459.5≤x＜549.5
4
分档
户年用气量（m3）
销售价格(元/m3)
第一档
0-350(含)
2.61
第二档
350-500(含)
2.83
第三档
500以上
4.23
题号
1
2
3
4
5
6
7
8
9
10
答案
B
D
C
D
A
C
D
A
C
B
月用气量分组
(立方米)
划记
频数
9.5≤x＜99.5
4
99.5≤x＜189.5
12
189.5≤x＜279.5
36
279.5≤x＜369.5
18
369.5≤x＜459.5
6
459.5≤x＜549.5
4