

中考数学压轴真题汇编(全国通用)专题04二次函数中角度问题压轴真题训练(原卷版+解析)
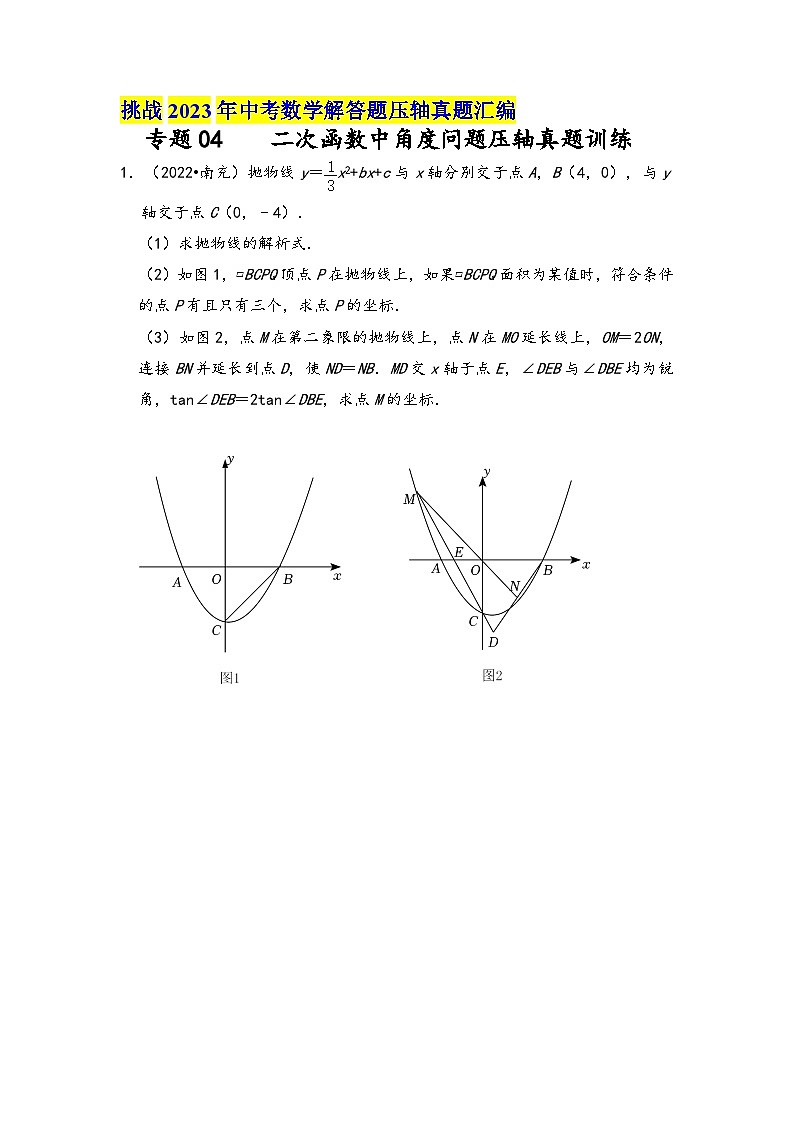
展开1.(2022•南充)抛物线y=x2+bx+c与x轴分别交于点A,B(4,0),与y轴交于点C(0,﹣4).
(1)求抛物线的解析式.
(2)如图1,▱BCPQ顶点P在抛物线上,如果▱BCPQ面积为某值时,符合条件的点P有且只有三个,求点P的坐标.
(3)如图2,点M在第二象限的抛物线上,点N在MO延长线上,OM=2ON,连接BN并延长到点D,使ND=NB.MD交x轴于点E,∠DEB与∠DBE均为锐角,tan∠DEB=2tan∠DBE,求点M的坐标.
2.(2022•益阳)如图,在平面直角坐标系xOy中,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P在抛物线F:y=ax2上,直线x=t与抛物线E,F分别交于点A,B.
(1)求a的值;
(2)将A,B的纵坐标分别记为yA,yB,设s=yA﹣yB,若s的最大值为4,则m的值是多少?
(3)Q是x轴的正半轴上一点,且PQ的中点M恰好在抛物线F上.试探究:此时无论m为何负值,在y轴的负半轴上是否存在定点G,使∠PQG总为直角?若存在,请求出点G的坐标;若不存在,请说明理由.
3.(2022•西宁)如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),与y轴交于点B,点C在直线AB上,过点C作CD⊥x轴于点D(1,0),将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处.
(1)求抛物线解析式;
(2)连接BE,求△BCE的面积;
(3)抛物线上是否存在一点P,使∠PEA=∠BAE?若存在,求出P点坐标;若不存在,请说明理由.
4.(2022•湖北)抛物线y=x2﹣4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.
(1)直接写出点B和点D的坐标;
(2)如图1,连接OD,P为x轴上的动点,当tan∠PDO=时,求点P的坐标;
(3)如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2,求的最大值.
5.(2022•苏州)如图,二次函数y=﹣x2+2mx+2m+1(m是常数,且m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.其对称轴与线段BC交于点E,与x轴交于点F.连接AC,BD.
(1)求A,B,C三点的坐标(用数字或含m的式子表示),并求∠OBC的度数;
(2)若∠ACO=∠CBD,求m的值;
(3)若在第四象限内二次函数y=﹣x2+2mx+2m+1(m是常数,且m>0)的图象上,始终存在一点P,使得∠ACP=75°,请结合函数的图象,直接写出m的取值范围.
6.(2022•黄石)如图,抛物线y=﹣x2+x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C三点的坐标为 , , .
(2)连接AP,交线段BC于点D,
①当CP与x轴平行时,求的值;
②当CP与x轴不平行时,求的最大值;
(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.
7.(2022•锦州)如图,抛物线y=ax2+bx+3交x轴于点A(3,0)和点B(﹣1,0),交y轴于点C.
(1)求抛物线的表达式;
(2)D是直线AC上方抛物线上一动点,连接OD交AC于点N,当的值最大时,求点D的坐标;
(3)P为抛物线上一点,连接CP,过点P作PQ⊥CP交抛物线对称轴于点Q,当tan∠PCQ=时,请直接写出点P的横坐标.
8.(2022•西宁)如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),与y轴交于点B,点C在直线AB上,过点C作CD⊥x轴于点D(1,0),将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处.
(1)求抛物线解析式;
(2)连接BE,求△BCE的面积;
(3)抛物线上是否存在一点P,使∠PEA=∠BAE?若存在,求出P点坐标;若不存在,请说明理由.
9.(2022•盘锦)如图,抛物线y=x2+bx+c与x轴交于A,B(4,0)两点(A在B的左侧),与y轴交于点C(0,﹣4).点P在抛物线上,连接BC,BP.
(1)求抛物线的解析式;
(2)如图1,若点P在第四象限,点D在线段BC上,连接PD并延长交x轴于点E,连接CE,记△DCE的面积为S1,△DBP的面积为S2,当S1=S2时,求点P的坐标;
(3)如图2,若点P在第二象限,点F为抛物线的顶点,抛物线的对称轴l与线段BC交于点G,当∠PBC+∠CFG=90°时,求点P的横坐标.
10.(2022•新市区校级三模)综合与探究
如图,抛物线与x轴交于点A(﹣1,0)和点B(4,0),与y轴交于点C,连接BC.
(1)求抛物线的表达式及点C的坐标;
(2)点P是抛物线对称轴上一点,点Q为平面内一点,当以点B、C、P、Q为顶点的四边形是以BC为边的矩形时,请直接写出点P的坐标;
(3)点D是第四象限内抛物线上一动点,当∠BCD=2∠ABC时,求点D的坐标.
挑战2023年中考数学解答题压轴真题汇编
专题04 二次函数中角度问题压轴真题训练
1.(2022•南充)抛物线y=x2+bx+c与x轴分别交于点A,B(4,0),与y轴交于点C(0,﹣4).
(1)求抛物线的解析式.
(2)如图1,▱BCPQ顶点P在抛物线上,如果▱BCPQ面积为某值时,符合条件的点P有且只有三个,求点P的坐标.
(3)如图2,点M在第二象限的抛物线上,点N在MO延长线上,OM=2ON,连接BN并延长到点D,使ND=NB.MD交x轴于点E,∠DEB与∠DBE均为锐角,tan∠DEB=2tan∠DBE,求点M的坐标.
【解答】解:(1)由题意得,
,
∴,
∴y=﹣;
(2)如图1,
作直线l∥BC且与抛物线相切于点P1,直线l交y轴于E,作直线m∥BC且直线m到BC的距离等于直线l到BC的距离,
∵BC的解析式为y=x﹣4,
∴设直线l的解析式为:y=x+m,
由=x+m得,
x2﹣4x﹣3(m+4)=0,
∵Δ=0,
∴﹣3(m+4)=4,
∴m=﹣,
∴x2﹣4x+4=0,y=x﹣,
∴x=2,y=﹣,
∴P1(2,﹣),
∵E(0,﹣),C(0,﹣4),
∴F(0,﹣4×2﹣(﹣)),
即(0,﹣),
∴直线m的解析式为:y=x﹣,
∴,
∴,,
∴P2(2﹣2,﹣2﹣),P3(2+2,2﹣),
综上所述:点P(2,﹣)或(2﹣2,﹣2﹣)或(2+2,2﹣);
(3)如图2,
作MG⊥x轴于G,作NH⊥x轴于H,作MK⊥DF,交DF的延长线于K,
设D点的横坐标为a,
∵BN=DN,
∴BD=2BN,N点的横坐标为:,
∴OH=,
∵NH∥DF,
∴△BHN∽△BFD,
∴,
∴DF=2NH,
同理可得:△OMG∽△ONH,
∴=,
∴MG=2NH,OG=2OH=a+4,
∴KF=MG=DF,
∵tan∠DEB=2tan∠DBE
∴=2•,
∴EF=,
∵BF=4﹣a,
∴EF=,
∵EF∥MK,
∴△DEF∽△DMK,
∴=,
∴,
∴a=0,
∴OG=a+4=4,
∴G(﹣4,0),
当x=﹣4时,y=﹣﹣4=,
∴M(﹣4,).
2.(2022•益阳)如图,在平面直角坐标系xOy中,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P在抛物线F:y=ax2上,直线x=t与抛物线E,F分别交于点A,B.
(1)求a的值;
(2)将A,B的纵坐标分别记为yA,yB,设s=yA﹣yB,若s的最大值为4,则m的值是多少?
(3)Q是x轴的正半轴上一点,且PQ的中点M恰好在抛物线F上.试探究:此时无论m为何负值,在y轴的负半轴上是否存在定点G,使∠PQG总为直角?若存在,请求出点G的坐标;若不存在,请说明理由.
【解答】解:(1)由题意可知,抛物线E:y=﹣(x﹣m)2+2m2(m<0)的顶点P的坐标为(m,2m2),
∵点P在抛物线F:y=ax2上,
∴am2=2m2,
∴a=2.
(2)∵直线x=t与抛物线E,F分别交于点A,B,
∴yA=﹣(t﹣m)2+2m2=﹣t2+2mt+m2,yB=2t2,
∴s=yA﹣yB
=﹣t2+2mt+m2﹣2t2
=﹣3t2+2mt+m2
=﹣3(t﹣m)2+m2,
∵﹣3<0,
∴当t=m时,s的最大值为m2,
∵s的最大值为4,
∴m2=4,解得m=±,
∵m<0,
∴m=﹣.
(3)存在,理由如下:
设点M的横坐标为n,则M(n,2n2),
∴Q(2n﹣m,4n2﹣2m2),
∵点Q在x轴正半轴上,
∴2n﹣m>0且4n2﹣2m2=0,
∴n=﹣m,
∴M(﹣m,m2),Q(﹣m﹣m,0).
如图,过点Q作x轴的垂线KN,分别过点P,G作x轴的平行线,与KN分别交于K,N,
∴∠K=∠N=90°,∠QPK+∠PQK=90°,
∵∠PQG=90°,
∴∠PQK+∠GQN=90°,
∴∠QPK=∠GQN,
∴△PKQ∽△QNG,
∴PK:QN=KQ:GN,即PK•GN=KQ•QN.
∵PK=﹣m﹣m﹣m=﹣m﹣2m,KQ=2m2,GN=﹣m﹣m,
∴(﹣m﹣2m)(﹣m﹣m)=2m2•QN
解得QN=.
∴G(0,﹣).
3.(2022•西宁)如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),与y轴交于点B,点C在直线AB上,过点C作CD⊥x轴于点D(1,0),将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处.
(1)求抛物线解析式;
(2)连接BE,求△BCE的面积;
(3)抛物线上是否存在一点P,使∠PEA=∠BAE?若存在,求出P点坐标;若不存在,请说明理由.
【解答】解:(1)∵将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处,点A的坐标为(3,0),点D的坐标为(1,0),
∴点E的坐标为(﹣1,0).
将A(3,0),E(﹣1,0)代入y=ax2+bx+3,
得:,解得:,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)当x=0时,y=﹣1×02+2×0+3=3,
∴点B的坐标为(0,3).
设直线AB的解析式为y=mx+n(m≠0),
将A(3,0),B(0,3)代入y=mx+n,
得:,解得:,
∴直线AB的解析式为y=﹣x+3.
∵点C在直线AB上,CD⊥x轴于点D(1,0),当x=1时,y=﹣1×1+3=2,
∴点C的坐标为(1,2).
∵点A的坐标为(3,0),点B的坐标为(0,3),点C的坐标为(1,2),点E的坐标为(﹣1,0),
∴AE=4,OB=3,CD=2,
∴S△BCE=S△ABE﹣S△ACE=AE•OB﹣AE•CD=×4×3﹣×4×2=2,
∴△BCE的面积为2.
(3)存在,理由如下:
∵点A的坐标为(3,0),点B的坐标为(0,3),
∴OA=OB=3.
在Rt△AOB中,∠AOB=90°,OA=OB,
∴∠BAE=45°.
∵点P在抛物线上,
∴设点P的坐标为(m,﹣m2+2m+3).
①当点P在x轴上方时记为P1,过点P1作P1M⊥x轴于点M,
在Rt△EMP1中,∠P1EA=45°,∠P1ME=90°,
∴EM=P1M,即m﹣(﹣1)=﹣m2+2m+3,
解得:m1=﹣1(不合题意,舍去),m2=2,
∴点P1的坐标为(2,3);
②当点P在x轴下方时记为P2,过点P2作P2N⊥x轴于点N,
在Rt△ENP2中,∠P2EN=45°,∠P2NE=90°,
∴EN=P2N,即m﹣(﹣1)=﹣(﹣m2+2m+3),
解得:m1=﹣1(不合题意,舍去),m2=4,
∴点P2的坐标为(4,﹣5).
综上所述,抛物线上存在一点P,使∠PEA=∠BAE,点P的坐标为(2,3)或(4,﹣5).
4.(2022•湖北)抛物线y=x2﹣4x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.
(1)直接写出点B和点D的坐标;
(2)如图1,连接OD,P为x轴上的动点,当tan∠PDO=时,求点P的坐标;
(3)如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2,求的最大值.
【解答】解:(1)令y=x2﹣4x=x,
解得x=0或x=5,
∴B(5,5);
∵y=x2﹣4x=(x﹣2)2﹣4,
∴顶点D(2,﹣4).
(2)如图,过点D作DE⊥y轴于点E,
∴DE=2,OE=4,
∴tan∠DOE=,
∵tan∠PDO=,
∴∠DOE=∠PDO,
①当点P在线段OD的右侧时,DP∥y轴,如图,
∴P(2,0);
②当点P在线段OD左侧时,设直线DP与y轴交于点G,则△ODG是等腰三角形,
∴OG=DG,
设OG=t,则DG=t,GE=4﹣t,
在Rt△DGE中,t2=22+(4﹣t)2,
解得t=,
∴G(0,﹣),
∴直线DG的解析式为:y=﹣x﹣,
令y=0,则﹣x﹣=0,
解得x=﹣,
∴P(﹣,0).
综上,点P的坐标为(2,0)或(﹣,0).
(3)∵点B(5,5)与点M关于对称轴x=2对称,
∴M(﹣1,5).
如图,分别过点M,Q作y轴的平行线,交直线OB于点N,K,
∴N(﹣1,﹣1),MN=6,
∵点Q横坐标为m,
∴Q(m,m2﹣4m),K(m,m),
∴KQ=m﹣(m2﹣4m)=﹣m2+5m.
∵S1=QK(xB﹣xE),S2=MN(xB﹣xE),
∴==﹣(m2﹣5m)=﹣(m﹣)2+,
∵﹣<0,
∴当m=时,的最大值为.
提示:本题也可分别过点M,Q作BO的垂线,用m分别表示高线,再求比,也可得出结论.
5.(2022•苏州)如图,二次函数y=﹣x2+2mx+2m+1(m是常数,且m>0)的图象与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为D.其对称轴与线段BC交于点E,与x轴交于点F.连接AC,BD.
(1)求A,B,C三点的坐标(用数字或含m的式子表示),并求∠OBC的度数;
(2)若∠ACO=∠CBD,求m的值;
(3)若在第四象限内二次函数y=﹣x2+2mx+2m+1(m是常数,且m>0)的图象上,始终存在一点P,使得∠ACP=75°,请结合函数的图象,直接写出m的取值范围.
【解答】解:(1)当y=0时,﹣x2+2mx+2m+1=0,
解方程,得x1=﹣1,x2=2m+1,
∵点A在点B的左侧,且m>0,
∴A(﹣1,0),B(2m+1,0),
当x=0时,y=2m+1,
∴C(0,2m+1),
∴OB=OC=2m+1,
∵∠BOC=90°,
∴∠OBC=45°;
(2)如图1中,连接AE.
∵y=﹣x2+2mx+2m+1=﹣(x﹣m)2+(m+1)2,
∴D(m,(m+1)2),F(m,0),
∴DF=(m+1)2,OF=m,BF=m+1,
∵A,B关于对称轴对称,
∴AE=BE,
∴∠EAB=∠OBC=45°,
∵∠ACO=∠CBD,∠OCB=∠OBC,
∴∠ACO+∠OCB=∠CBD+∠OBC,即∠ACE=∠DBF,
∵EF∥OC,
∴tan∠ACE====,
∴=m+1,
∴m=1或﹣1,
∵m>0,
∴m=1;
(3)如图,设PC交x轴于点Q.
当点P在第四象限时,点Q总是在点B的左侧,此时∠CQA>∠CBA,即∠CQA>45°,
∵∠ACQ=75°,
∴∠CAO<60°,
∴2m+1<,
∴m<,
又∵∠CAQ>15°,
同法可得m>,
∵m>0,
∴0<m<.
6.(2022•黄石)如图,抛物线y=﹣x2+x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
(1)A,B,C三点的坐标为 , , .
(2)连接AP,交线段BC于点D,
①当CP与x轴平行时,求的值;
②当CP与x轴不平行时,求的最大值;
(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.
【解答】解:(1)令x=0,则y=4,
∴C(0,4);
令y=0,则﹣x2+x+4=0,
∴x=﹣2或x=3,
∴A(﹣2,0),B(3,0).
故答案为:(﹣2,0);(3,0);(0,4).
(2)①∵CP∥x轴,C(0,4),
∴P(1,4),
∴CP=1,AB=5,
∵CP∥x轴,
∴==.
②如图,过点P作PQ∥AB交BC于点Q,
∴直线BC的解析式为:y=﹣x+4.
设点P的横坐标为m,
则P(m,﹣m2+m+4),Q(m2﹣m,﹣m2+m+4).
∴PQ=m﹣(m2﹣m)=﹣m2+m,
∵PQ∥AB,
∴===﹣(m﹣)2+,
∴当m=时,的最大值为.
另解:分别过点P,A作y轴的平行线,交直线BC于两点,仿照以上解法即可求解.
(3)假设存在点P使得∠BCO+2∠BCP=90°,即0<m<3.
过点C作CF∥x轴交抛物线于点F,
∵∠BCO+2∠PCB=90°,∠BCO+∠BCM+∠MCF=90°,
∴∠MCF=∠BCP,
延长CP交x轴于点M,
∵CF∥x轴,
∴∠PCF=∠BMC,
∴∠BCP=∠BMC,
∴△CBM为等腰三角形,
∵BC=5,
∴BM=5,OM=8,
∴M(8,0),
∴直线CM的解析式为:y=﹣x+4,
令﹣x2+x+4=﹣x+4,
解得x=或x=0(舍),
∴存在点P满足题意,此时m=.
7.(2022•锦州)如图,抛物线y=ax2+bx+3交x轴于点A(3,0)和点B(﹣1,0),交y轴于点C.
(1)求抛物线的表达式;
(2)D是直线AC上方抛物线上一动点,连接OD交AC于点N,当的值最大时,求点D的坐标;
(3)P为抛物线上一点,连接CP,过点P作PQ⊥CP交抛物线对称轴于点Q,当tan∠PCQ=时,请直接写出点P的横坐标.
【解答】解:(1)把点A(3,0)和B(﹣1,0)代入得:,
解得:,
∴抛物线的解析式为y=﹣x2+2x+3;
(2)过点D作DH∥y轴,交AC于点H,如图所示:
设D(m,﹣m2+2m+3),直线AC的解析式为y=kx+b,
由(1)可得:C(0,3),
∴,解得:,
∴直线AC的解析式为y=﹣x+3,
∴H(m,﹣m+3),
∴DH=﹣m2+3m,
∵DH∥y轴,
∴△OCN∽△DHN,
∴,
∵,
∴当时,的值最大,
∴;
(3)由题意可得如图所示:
过点P作y轴的平行线PH,分别过点C、Q作CG⊥PH于G,QH⊥PH于H,
∵PQ⊥CP,
∴∠CPQ=∠CGP=∠PHQ=90°,
∴∠CPG+∠PCG=∠CPG+∠QPH=90°,
∴∠PCG=∠QPH,
∴△PCG∽△QPH,
∴,
∵,
∴,
设点P(n,﹣n2+2n+3),
由题意可知:抛物线的对称轴为直线x=1,C(0,3),
∴QH=|n﹣1|,PG=|﹣n2+2n|,
∴,
当时,解得:,
当时,解得:
综上:点P的横坐标为或或或.
8.(2022•西宁)如图,抛物线y=ax2+bx+3与x轴交于点A(3,0),与y轴交于点B,点C在直线AB上,过点C作CD⊥x轴于点D(1,0),将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处.
(1)求抛物线解析式;
(2)连接BE,求△BCE的面积;
(3)抛物线上是否存在一点P,使∠PEA=∠BAE?若存在,求出P点坐标;若不存在,请说明理由.
【解答】解:(1)∵将△ACD沿CD所在直线翻折,使点A恰好落在抛物线上的点E处,点A的坐标为(3,0),点D的坐标为(1,0),
∴点E的坐标为(﹣1,0).
将A(3,0),E(﹣1,0)代入y=ax2+bx+3,
得:,解得:,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)当x=0时,y=﹣1×02+2×0+3=3,
∴点B的坐标为(0,3).
设直线AB的解析式为y=mx+n(m≠0),
将A(3,0),B(0,3)代入y=mx+n,
得:,解得:,
∴直线AB的解析式为y=﹣x+3.
∵点C在直线AB上,CD⊥x轴于点D(1,0),当x=1时,y=﹣1×1+3=2,
∴点C的坐标为(1,2).
∵点A的坐标为(3,0),点B的坐标为(0,3),点C的坐标为(1,2),点E的坐标为(﹣1,0),
∴AE=4,OB=3,CD=2,
∴S△BCE=S△ABE﹣S△ACE=AE•OB﹣AE•CD=×4×3﹣×4×2=2,
∴△BCE的面积为2.
(3)存在,理由如下:
∵点A的坐标为(3,0),点B的坐标为(0,3),
∴OA=OB=3.
在Rt△AOB中,∠AOB=90°,OA=OB,
∴∠BAE=45°.
∵点P在抛物线上,
∴设点P的坐标为(m,﹣m2+2m+3).
①当点P在x轴上方时记为P1,过点P1作P1M⊥x轴于点M,
在Rt△EMP1中,∠P1EA=45°,∠P1ME=90°,
∴EM=P1M,即m﹣(﹣1)=﹣m2+2m+3,
解得:m1=﹣1(不合题意,舍去),m2=2,
∴点P1的坐标为(2,3);
②当点P在x轴下方时记为P2,过点P2作P2N⊥x轴于点N,
在Rt△ENP2中,∠P2EN=45°,∠P2NE=90°,
∴EN=P2N,即m﹣(﹣1)=﹣(﹣m2+2m+3),
解得:m1=﹣1(不合题意,舍去),m2=4,
∴点P2的坐标为(4,﹣5).
综上所述,抛物线上存在一点P,使∠PEA=∠BAE,点P的坐标为(2,3)或(4,﹣5).
9.(2022•盘锦)如图,抛物线y=x2+bx+c与x轴交于A,B(4,0)两点(A在B的左侧),与y轴交于点C(0,﹣4).点P在抛物线上,连接BC,BP.
(1)求抛物线的解析式;
(2)如图1,若点P在第四象限,点D在线段BC上,连接PD并延长交x轴于点E,连接CE,记△DCE的面积为S1,△DBP的面积为S2,当S1=S2时,求点P的坐标;
(3)如图2,若点P在第二象限,点F为抛物线的顶点,抛物线的对称轴l与线段BC交于点G,当∠PBC+∠CFG=90°时,求点P的横坐标.
【解答】解:(1)将B(4,0)、C(0,﹣4)两点代入y=x2+bx+c得,
,
解得:,
∴抛物线的解析式为:y=x2﹣3x﹣4;
(2)方法一:由y=x2﹣3x﹣4可得,A(﹣1,0),
设点P(m,m2﹣3m﹣4),
则,,
∵S△BCE=S1+S△BDE,S△BPE=S2+S△BDE,S1=S2,
∴S△BCE=S△BPE,
∴,
解得:m1=3,m2=0(舍去),
∴P(3,﹣4);
方法二:∵S1=S2,
∴S△PBE=S△CBE,
∴PC∥x轴,
∴点P与C关于对称轴x=对称,
∴P(3,﹣4);
(3)如图,作CE⊥l于E,PQ⊥BC于Q,PN⊥x轴于N,连接PC交x轴于点H,
设P(n,n2﹣3n﹣4),PC的表达式为:y=kx+d(k≠0),
将P,C代入y=kx+d(k≠0)得,
,
解得:,
∴PC的表达式为:y=(n﹣3)x﹣4,
将y=0代入y=(n﹣3)x﹣4得,
0=(n﹣3)x﹣4,
即,
∴,
∵S△PCB=S△PHB+S△HCB,
∴PQ•BC=PN•HB+OC•HB,
∵BC==,
∴,
∵,
由题可知,,
∴,
将代入y=x2﹣3x﹣4得,,
∴,
∴,
∵∠PBC+∠CFG=90°,PQ⊥BC,CE⊥l,
∴∠PBQ=∠FCE,∠CEF=∠PQB,
∴△CEF∽△PQB,
∴,
∴,
解得:(舍去).
∴点P的横坐标为﹣,
方法二:将CF绕点F顺时针旋转90°得C',连接CC',作CE⊥l于E,
求出点C'(),
从而求出直线CC'的解析式,
∴∠ECF=∠BCC'=∠PBC,
∴BP∥CC',
求出直线BP的解析式与抛物线求交点即可.
10.(2022•新市区校级三模)综合与探究
如图,抛物线与x轴交于点A(﹣1,0)和点B(4,0),与y轴交于点C,连接BC.
(1)求抛物线的表达式及点C的坐标;
(2)点P是抛物线对称轴上一点,点Q为平面内一点,当以点B、C、P、Q为顶点的四边形是以BC为边的矩形时,请直接写出点P的坐标;
(3)点D是第四象限内抛物线上一动点,当∠BCD=2∠ABC时,求点D的坐标.
【解答】解:(1)由题意得:y=(x+1)(x﹣4)=x2﹣x﹣2;
当x=0时,y=﹣2,即点C(0,﹣2);
(2)以点B、C、P、Q为顶点的四边形是以BC为边的矩形时,如下图,分点P在BC上方和下方两种情况,
当点P在BC的上方时,设抛物线的对称轴交x轴于点H,
∵∠OBC+∠PBH=90°,∠HPB+∠PBH=90°,
∴∠OBC=∠HPB,
∴∠OBC=∠HPB=,解得:PH=5,
即点P(,5);
当点P在BC的下方时,过点P作PH⊥y轴于点H,
同理可得:tan∠HCP=tan∠OBC=,
即,即,
解得:HC=3,则OH=5,
即点P(,﹣5);
综上,点P的坐标为:(,5)或(,﹣5);
(3)作点C关于x轴的对称点E(0,2),则∠CBE=2∠ABC=∠BCD,
∴BE∥CD,
设直线BE的表达式为:y=kx+2,
将点B的坐标代入上式得:0=4k+2,解得:k=﹣;
∵BE∥CD,
故设直线CD的表达式为:y=﹣x+t,
由点C的坐标知,t=﹣2,
即直线CD的表达式为:y=﹣x﹣2,
联立y=x2﹣x﹣2和y=﹣x﹣2,并解得:x=0(舍去)或2,
即点D(2,﹣3).
最新中考数学压轴真题汇编 专题05 二次函数函数综合的压轴真题训练 (全国通用): 这是一份最新中考数学压轴真题汇编 专题05 二次函数函数综合的压轴真题训练 (全国通用),文件包含专题05二次函数函数综合的压轴真题训练原卷版docx、专题05二次函数函数综合的压轴真题训练解析版docx等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。
最新中考数学压轴真题汇编 专题04 反比例函数综合的压轴真题训练 (全国通用): 这是一份最新中考数学压轴真题汇编 专题04 反比例函数综合的压轴真题训练 (全国通用),文件包含专题04反比例函数综合的压轴真题训练原卷版docx、专题04反比例函数综合的压轴真题训练解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
最新中考数学压轴真题汇编 专题03 二次函数中面积问题压轴真题训练 (全国通用): 这是一份最新中考数学压轴真题汇编 专题03 二次函数中面积问题压轴真题训练 (全国通用),文件包含专题03二次函数中面积问题压轴真题训练原卷版docx、专题03二次函数中面积问题压轴真题训练解析版docx等2份试卷配套教学资源,其中试卷共82页, 欢迎下载使用。












