

2023-2024学年新疆乌鲁木齐十九中高一(下)第二次月考数学试卷(含答案)
展开
这是一份2023-2024学年新疆乌鲁木齐十九中高一(下)第二次月考数学试卷(含答案),共8页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
1.复数z=1−i3−i的共轭复数的模是( )
A. 15B. 55C. 2 55D. 25
2.下列说法正确的是( )
A. 若直线l与平面α内的无数条直线垂直,则l⊥α
B. 若a⊥b,b⊥α,则a//α
C. 若直线l与平面α垂直,则直线l与平面α内所有直线所成的角均为90°
D. 若直线l与平面α所成的角为0°,则直线l//平面α
3.如图是一个圆台的侧面展开图,已知BA=12,BD=6且∠ABC=120°,则该圆台的体积为( )
A. 112 2π
B. 7 23π
C. 28 23π
D. 112 23π
4.已知m是直线,α,β是两个不同的平面,下列正确的命题是( )
A. 若m//β,α//β,则m//αB. 若m⊥β,α⊥β,则m//α
C. 若m//β,α⊥β,则m⊥αD. 若m//β,m⊥α,则α⊥β
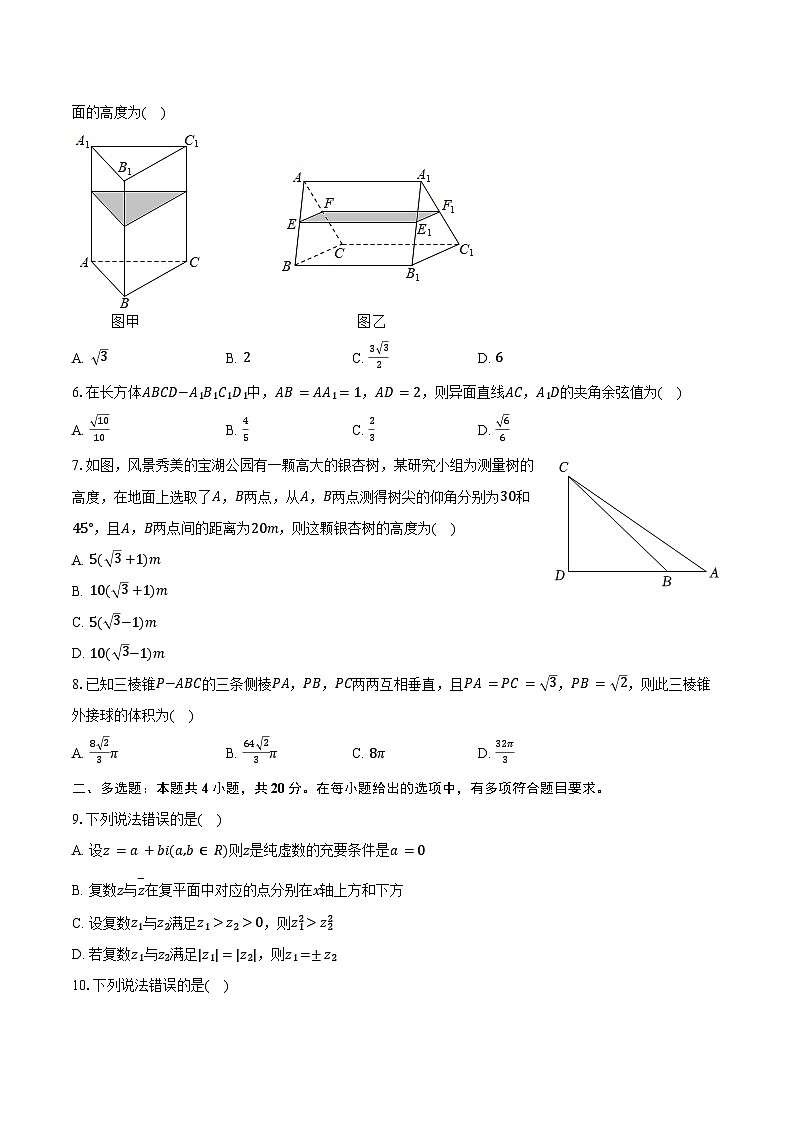
5.一个封闭的正三棱柱容器,高为8,内装水若干(如图甲,底面处于水平状态).将容器放倒(如图乙,一个侧面处于水平状态),这时水面所在的平面与各棱交点E,F,F1,E1分别为所在的棱的中点,则图甲中水面的高度为( )
A. 3B. 2C. 3 32D. 6
6.在长方体ABCD−A1B1C1D1中,AB=AA1=1,AD=2,则异面直线AC,A1D的夹角余弦值为( )
A. 1010B. 45C. 23D. 66
7.如图,风景秀美的宝湖公园有一颗高大的银杏树,某研究小组为测量树的高度,在地面上选取了A,B两点,从A,B两点测得树尖的仰角分别为30和45°,且A,B两点间的距离为20m,则这颗银杏树的高度为( )
A. 5( 3+1)m
B. 10( 3+1)m
C. 5( 3−1)m
D. 10( 3−1)m
8.已知三棱锥P−ABC的三条侧棱PA,PB,PC两两互相垂直,且PA=PC= 3,PB= 2,则此三棱锥外接球的体积为( )
A. 8 23πB. 64 23πC. 8πD. 32π3
二、多选题:本题共4小题,共20分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法错误的是( )
A. 设z=a+bi(a,b∈R)则z是纯虚数的充要条件是a=0
B. 复数z与z−在复平面中对应的点分别在x轴上方和下方
C. 设复数z1与z2满足z1>z2>0,则z12>z22
D. 若复数z1与z2满足|z1|=|z2|,则z1=±z2
10.下列说法错误的是( )
A. 已知向量a=(2,3),b=(x,2),则“a,b的夹角为锐角”是“x>−3”的充要条件
B. 已知向量a=(1, 3),b=(csθ,sinθ),若a⊥b,则tanθ= 33
C. 若向量a=(−4,3),b=(1,3),则a在b方向上的投影向量坐标为(12,32)
D. 在△ABC中,向量AB与AC满足(AB|AB|+AC|AC|)⋅BC=0,则△ABC为等边三角形
11.在△ABC中,角A,B,C的对边分别为a,b,c,则下列结论正确的是( )
A. 若a2+b2csB
12.正方体ABCD−A1B1C1D1的棱长为2,E,F,G分别为BC,CC1,BB1的中点,则( )
A. 直线DD1与直线AF垂直
B. 直线A1G与平面AEF平行
C. 平面AEF截正方体所得的截面面积为92
D. 点A1和点D到平面AEF的距离不相等
三、填空题:本题共4小题,每小题5分,共20分。
13.水平放置的△ABC的斜二测直观图△A′B′C′如图所示,已知A′C′=3,B′C′=2,则△ABC的面积为______.
14.已知e1,e2是两个不共线的向量,a=e1−4e2,b=ke1+2e2,若a与b共线,则k= ______.
15.一个圆柱和一个圆锥的轴截面分别是边长为a的正方形和正三角形,则它们的表面积之比为 .
16.已知过球面上A,B,C三点的截面和球心的距离等于球半径的一半,且AB=18,BC=24,AC=30,则球的表面积为______.
四、解答题:本题共5小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题12分)
在△ABC中,角A,B,C所对的边分别为a,b,c,且(2a− 3c)csB= 3bcsC.
(1)求B;
(2)BC=2 3,D为边AB上一点,BD=1,∠ACD=π2,求AC长.
18.(本小题12分)
某灯具配件厂生产了一种塑胶配件,该厂质检人员某日随机抽取了100个该配件的质量指标值(单位:分)作为一个样本,得到如下所示的频率分布直方图,则(同一组中的数据用该组区间的中点值作代表)
(1)求出m的值;
(2)求样本质量指标值的平均数,众数;
(3)求样本质量指标值的第75百分位数.
19.(本小题12分)
已知平行四边形ABCD中,AB=3,BC=6,∠DAB=60°,点E是线段BC的中点.
(1)求AB⋅AD的值;
(2)若AF=AE+λAD,且BD⊥AF,求λ的值.
20.(本小题17分)
《九章算术》中对一些特殊的几何体有特殊的称谓,例如,将底面为直角三角形的直三棱柱叫堑堵,将一个堑堵沿其一顶点与相对的棱刨开,得到一个阳马(底面是长方形,且有一条侧棱与底面垂直的四棱锥,即四棱锥C1−ABB1A1)和一个鳖臑(四个面均为直角三角形的四面体,即三棱锥C1−ABC).在如图所示的堑堵ABC−A1B1C1中,已知AB=3,BC=4,AC=5,若鳖臑C1−ABC的体积等于12,求:
(1)求堑堵ABC−A1B1C1的侧棱长;
(2)求阳马C1−ABB1A1的体积;
(3)求阳马C1−ABB1A1的表面积.
21.(本小题17分)
如图,已知AA1⊥平面ABC,BB1//AA1,AB=AC=3,BC=2 5,AA1= 7,BB1=2 7,点E和F分别为BC和A1C的中点.
(1)求证:EF//平面A1B1BA;
(2)求证:AE⊥平面BCB1;
(3)求直线A1B1与平面BCB1所成角的大小.
参考答案
1.B
2.C
3.D
4.D
5.D
6.B
7.B
8.A
9.ABD
10.ABD
11.AD
12.BC
13.6
14.−12
15.2:1
16.1200π
17.解:(1)因为(2a− 3c)csB= 3bcsC,
则由正弦定理得:(2sinA− 3sinC)csB= 3sinBcsC,
⇒2sinAcsB= 3sinCcsB+ 3sinBcsC= 3sin(B+C)= 3sinA,
显然sinA≠0则csB= 32,
又B∈(0,π),故B=π6;
(2)因为BC=2 3,BD=1,B=π6,
根据余弦定理得:
CD2=BC2+BD2−2BC⋅BD⋅csB=1+12−2×1×2 3× 32=7,∴CD= 7.
所以cs∠BDC=DB2+DC2−BC22DB⋅DC=1+7−122×1× 7=2 77,
所以cs∠ADC=−cs∠BDC=2 77,
所以sin∠ADC= 1−(2 77)2= 217,
所以tan∠ADC= 32,
所以AC=CD⋅tan∠ADC= 7× 32= 212.
18.解:(1)由题意知(0.010+0.015+m+0.035+0.010)×10=1,解得m=0.030;
(2)样本质量指标值的平均数为55×0.1+65×0.15+75×0.35+85×0.3+95×0.1=76.5,
显然由图知,频率最高的为[70,80)之间,则样本质量指标值的众数是70+802=75;
(3)前3组的频率之和为(0.010+0.015+0.035)×10=0.60,
前4组的频率之和为0.60+0.030×10=0.90,
故第75百分位数位于第4组,设其为t,
则(t−80)×0.030+0.60=0.75,解得t=85,
即第75百分位数为85.
19.解:(1)以A点为坐标原点,AB所在直线为x轴,过A且垂直于AB的直线为y轴,建立如图所示的平面直角坐标系,
则A(0,0),C(6,3 3),E(92,3 32),B(3,0),D(3,3 3),
则AD=(3,3 3),AB=(3,0),
所以AB⋅AD=9;
(2)AF=AE+λAD=(92+3λ,32 3+3 3λ),BD=(0,3 3),
因为BD⊥AF,
所以BD⋅AF=3 3(32 3+3 3λ)=0,解得λ=−12.
20.解:(1)已知AB=3,BC=4,AC=5,
又ABC−A1B1C1为直棱柱,
设AA1=ℎ,
因为VC1−ABC=12,
所以13⋅12⋅4⋅3⋅ℎ=12,
所以ℎ=6;
(2)VC1−ABB1A1=13⋅3⋅6⋅4=24;
(3)SC1−ABB1A1=S△ABC1+S△B1BC1+S△A1AC1+S△B1B1C1+SB1BAA
=12⋅3⋅2 13+12⋅6⋅4+12⋅5⋅6+12⋅4⋅3+3⋅6
=51+3 13.
21.(1)证明:连接A1B,
在△A1BC中,∵E和F分别是BC和AlC的中点,∴EF//A1B,
又∵A1B⊂平面A1B1BA,EF⊄平面A1B1BA1,
∴EF//平面A1B1BA.
(2)证明:∵AB=AC,E为BC中点,∴AE⊥BC,
∵AA1⊥平面ABC,BB1//AA1,∴BB1⊥平面ABC,
又AE⊂平面ABC,
∴BB1⊥AE,
又∵BC∩BB1=B,BC,BB1⊂平面BCB1,∴AE⊥平面BCB1;
(3)解:取BB1中点M和B1C中点N,连接A1M,A1N,NE,
∵N和E分别为B1C和BC的中点,∴NE//B1B且NE=12B1B,
∴NE//A1A且NE=A1A,∴四边形A1AEN是平行四边形,
∴A1N//AE,
∵AE⊥平面BCB1,∴A1N⊥平面BCB1,
∴∠A1B1N即为直线A1B1与平面BCB1所成角,
在△ABC中,AE=2,∴A1N=AE=2,
∵BM//AA1,BM=AA1,∴A1M//AB且A1M=AB,
又由AB⊥BB1,∴A1M⊥BB1,
在RtΔA1MB1中,A1B1= B1M2+A1M2=4,
在Rt△A1NB1中,sin∠A1B1N=A1NA1B1=12,
因为∠A1B1N∈(0,π2],
∴∠A1B1N=π6,
即直线A1B1与平面BCB1所成角的大小为π6.
相关试卷
这是一份[数学]新疆乌鲁木齐市第十九中学2023-2024学年高一下学期4月月考试卷,共4页。试卷主要包含了填写答题卡的内容用2B铅笔填写,提前 xx 分钟收取答题卡等内容,欢迎下载使用。
这是一份[数学]新疆乌鲁木齐2023-2024数学年六十一中高一(下)期中数学试卷,共5页。试卷主要包含了填写答题卡的内容用2B铅笔填写,提前 xx 分钟收取答题卡等内容,欢迎下载使用。
这是一份2023-2024学年新疆乌鲁木齐六十一中高一(下)期中数学试卷(含解析),共13页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。









