

2023-2024学年江西省上饶市高二下学期期末教学质量检测数学试卷(含答案)
展开1.已知集合A={x|−8
2.已知数列{an}是等差数列,若a3+a7=14,则a1+a5+a9=( )
A. 14B. 21C. 28D. 42
3.“a+c>b+d”是“a>b且c>d”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充分必要条件D. 既不充分也不必要条件
4.设f(x)为R上的奇函数,且当x<0时,f(x)=3x−1,则f(0)+f(4)=( )
A. 12B. −12C. 13D. −13
5.函数f(x)=lnx+csπ3的导数f′(x)=( )
A. 1xB. 1x+sinπ3C. 1x−sin13D. x−π3
6.已知函数f(x)=lgax,x>1(2a−1)x+4a,x≤1在R上为减函数,则实数a的取值范围是( )
A. (0,12)B. (0,16]C. [16,+∞)D. [16,12)
7.己知a=0.4,b=e0.4−1,c=ln1.4,则a,b,c的大小关系为( )
A. a>c>bB. a>b>cC. b>a>cD. c>b>a
8.意大利数学家斐波那契(1175年∼1250年)以兔子繁殖数量为例,引入数列:1,1,2,3,5,8,…,该数列从第三项起,每一项都等于前两项之和,即an+2=an+1+an(n∈N∗),故此数列称为斐波那契数列,又称“兔子数列”,其通项公式为an=1 5[(1+ 52)n−(1− 52)n],设n是不等式lg2[(1+ 5)n−(1− 5)n]>n+5的正整数解,则n的最小值为( )
A. 6B. 7C. 8D. 9
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知函数y=fx的导函数f′x的图象如图所示,下列说法正确的是( )
A. 函数fx在2,+∞上单调递增B. 函数fx在1,3上单调递减
C. 函数fx在x=1处取得极大值D. 函数fx有最大值
10.下列说法正确的是( )
A. 设已知随机变量X,Y满足Y=3X−1,EY=5,则EX=2
B. 若X∼B10,15,则DX=2
C. 若X∼N2,σ2,设PX≥1=0.6,则PX≥3=0.4
D. 若事件A,B相互独立且0
A. f(x)的单调递增区间是(0,1)∪(1,+∞)
B. f(x)的值域为R
C. f(lg20232024)+f(lg20242023)=1
D. 若f(a)=eb+1eb−1−b,a∈(0,1),b∈(0,+∞),则aeb=1
三、填空题:本题共3小题,每小题5分,共15分。
12.某种产品的广告费支出x(单位:万元)与销售额y(单位:万元)之间有如下对应数据:
根据上表数据得到y关于x的经验回归方程y=4.5x+a,则a的值为 .
13.若f(x)=ln|a+11−x|+b是奇函数,则b= .
14.数列{an}中,a1=1,a2=2.设x=0是函数f(x)=an−1e2x+(an−an+1)x−2(n≥2且n∈N∗)的极值点.若[x]表示不超过x的最大整数,则[2024a1(a1+1)(2a1+1)+2024a2(a2+1)(2a2+1)+⋯+2024a2024(a2024+1)(2a2024+1)] = .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知函数f(x)=alnx+bx2−7x+12在点(1,f(1))处的切线方程为2x+y+3=0.
(1)求a,b;
(2)求f(x)的单调区间和极值.
16.(本小题15分)
求下列函数的最值.
(1)求函数y=x+1x−1(x>1)的最小值.
(2)已知0
已知等比数列{an}的前n项和为Sn,n∈N+,且Sn=32an−12.
(1)求数列{an}的通项公式;
(2)若bn=nan+1,求数列{bn}的前n项和Tn.
18.(本小题17分)
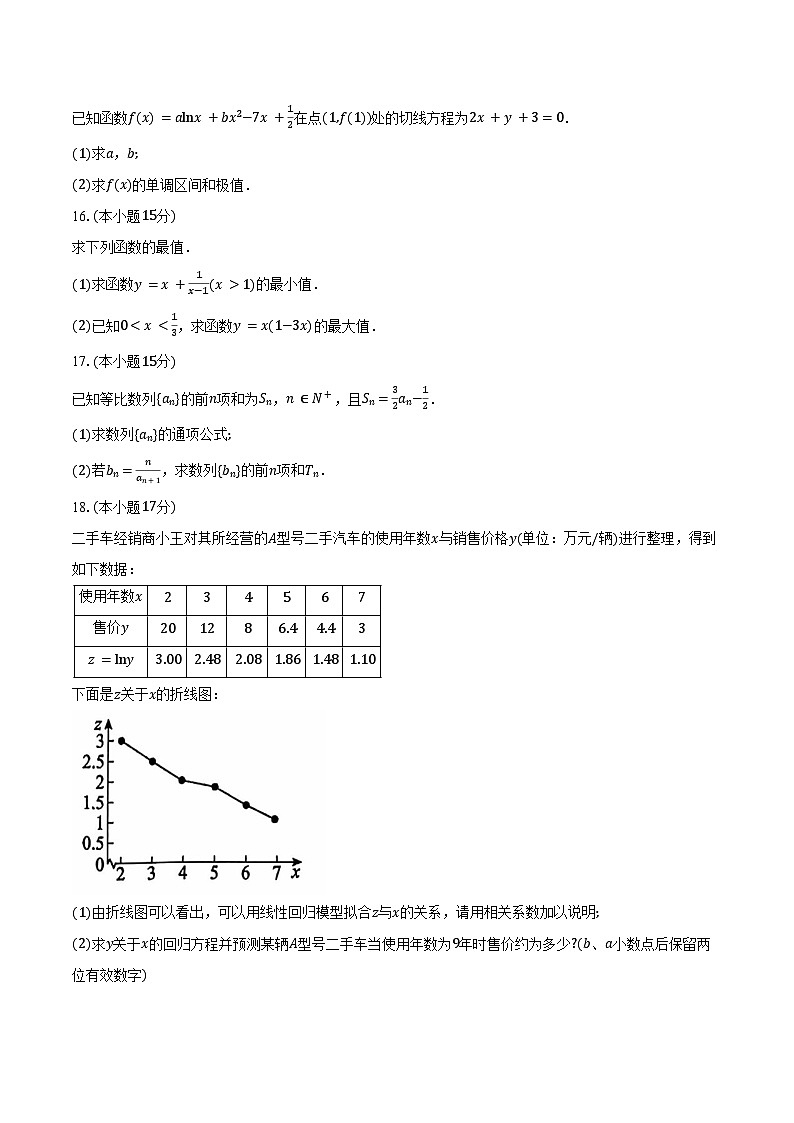
二手车经销商小王对其所经营的A型号二手汽车的使用年数x与销售价格y(单位:万元/辆)进行整理,得到如下数据:
下面是z关于x的折线图:
(1)由折线图可以看出,可以用线性回归模型拟合z与x的关系,请用相关系数加以说明;
(2)求y关于x的回归方程并预测某辆A型号二手车当使用年数为9年时售价约为多少?(b、a小数点后保留两位有效数字)
(3)基于成本的考虑,该型号二手车的售价不得低于7118元,请根据(2)求出的回归方程预测在收购该型号二手车时车辆的使用年数不得超过多少年?
参考数据:i=16xiyi=187.4,i=16xizi=47.64,i=16xi2=139, i=16(xi−x)2≈4.18, i=16(yi−y)2=13.96, i=16(zi−z)2=1.53,ln1.46≈0.38,ln0.7118≈−0.34.
参考公式:回归直线方程y=bx+a中b=i=1n(xi−x)(yi−y)i=1n(xi−x)2=i=1nxiyi−nx yi=1n(xi−nx)2,a=y−bx.r=i=1n(xi−x)(yi−y) i=1n(xi−x)2i=1n(yi−y)2,x、y为样本平均值.
19.(本小题17分)
函数f(x)=lnx−a(x−1)x+1.
(1)讨论f(x)的单调性;
(2)若函数f(x)有两个极值点x1,x2,曲线y=f(x)上两点(x1,f(x1)),(x2,f(x2))连线斜率记为k,求证:k>2−aa−1;
(3)盒子中有编号为1∼100的100个小球(除编号外无区别),有放回的随机抽取20个小球,记抽取的20个小球编号各不相同的概率为p,求证:p<1e2.
参考答案
1.C
2.B
3.B
4.C
5.A
6.D
7.C
8.C
9.BC
10.ACD
11.BD
12.12
13.ln2
14.1011
15.解:(1)定义域为(0,+∞),f′(x)=ax+2bx−7,
将点(1,f(1))代入2x+y+3=0中,
2×1+f(1)+3=0,∴f(1)=−5.
f(1)=b−7+12=5f′(1)=a+2b−7=−2⇒a=2b=32
(2)f(x)=2lnx+32x2−7x+12,
f′(x)=2x+3x−7=2+3x2−7x=(x−2)(3x−1)x,
f(x)的单调递增区间为(0,13),(2,+∞),单调递减区间为(13,2);
f(x)的极大值为f(13)=−53−2ln3,极小值为f(2)=−152+2ln2.
16.解:(1)∵x>1,∴x−1>0,
∴y=(x−1)+1x−1+1⩾2 (x−1)⋅1x−1+1=3,
故函数y的最小值为3,当且仅当(x−1)2=1,即x=2时取得;
(2)∵0
∴y=x(1−3x)
=13×3x(1−3x)
≤13[3x+1−3x2]2
=112,
当且仅当3x=1−3x,即x=16时,等号成立,y有最大值112.
17.解:(1)当n=1时,a1=32a1−12,得a1=1,
当n≥2时,Sn−Sn−1=an=32an−an−1 ,得an=3an−1,
∴数列an是公比为3的等比数列,
∴ an=3n−1(n∈N∗).
(2)由(1)得:bn=n3n,
又Tn=13+232+⋯+n3n,①
∴13Tn=132+233+⋯+n3n+1,②
两式相减得:23Tn=13+132+⋯+13n−n3n+1 ,
故23Tn=13(1−13n)1−13−n3n+1,
∴ Tn=34−3+2n4×3n.
18.解:(1)由题意,x−=16×(2+3+4+5+6+7)=4.5,
z−=16×(3+2.48+2.08+1.86+1.48+1.10)=2,
且i=16xizi=47.64, i=16(xi−x−)2≈4.18, i=16(zi−z−)2≈5.13,
∴r=i=16(xi−x−)(zi−z−) i=16(xi−x−)2i=16(zi−z−)2=47.64−6×4.5×24.18×1.53=−≈−0.99.
∴z与x的相关系数大约为−0.99,说明z与x的线性相关程度很高;
(2)∵b=i=16xizi−6x−z−i=16xi2−6x−2=47.64−6×4.5×2139−6×4.52=−6.3617.5≈−0.36,
a=z−−bx−=2+0.36×4.5=3.62,
∴z关于x的线性回归方程是z=−0.36x+3.62,
又z=ln y,
∴y关于x的回归方程是y=e−0.36x+3.62.
令x=9,解得y=e−0.36×9+3.62≈1.46,
即预测某辆A型号二手车当使用年数为9年时售价约1.46万元;
(3)当y≥0.7118时,e−0.36x+3.62≥0.7118=eln 0.7118=e−0.34,
∴−0.36x+3.62≥−0.34,解得x≤11,
因此预测在收购该型号二手车时车辆的使用年数不得超过11年.
19.解:(1)f(x)的定义域为(0,+∞),f′(x)=1x−a(x+1)−a(x−1)(x+1)2=x2+(2−2a)x+1x(x+1)2,
对于方程x2+(2−2a)x+1=0,△=(2−2a)2−4=4(a2−2a),
当Δ≤0,即0≤a≤2时,x2+(2−2a)x+1≥0,f′(x)≥0,f(x)在(0,+∞)上单调递增,
当△>0,即a<0或a>2时,方程x2+(2−2a)x+1=0有两个不等根,
x1=a−1− a2−2a,x2=a−1+ a2−2a,而x1+x2=2(a−1),x1x2=1,
所以当a<0时,x1
当a>2时,0
所以f(x)在(0,x1)和(x2,+∞)上单调递增,在(x1,x2)上单调递减.
综上,当a≤2时,f(x)在(0,+∞)上单调递增;
当a>2时,f(x)在(0,a−1− a2−2a)和(a−1+ a2−2a,+∞)上单调递增,
在(a−1− a2−2a,a−1+ a2−2a)上单调递减.
(2)由题,
所以要证k>2−aa−1,即证lnx1−lnx2x1−x2−1>1a−1−1,即证lnx1−lnx2x1−x2>2x1+x2,
也即证lnx1x2−2(x1−x2)x1+x2=lnx1x2−2x1x2−1x1x2+1<0(∗)成立.
设t=x1x2∈(0,1),函数ℎ(t)=lnt−2(t−1)t+1,
由(1)知ℎ(t)在(0,+∞)上单调递增,且ℎ(1)=0,
所以t∈(0,1)时,ℎ(t)<0,所以(∗)成立,原不等式得证.
(3)由题,p=A1002010020=100×99×⋯×82×8110020,
因为99×81=902−92<902,98×82=902−82<902,⋯,91×89=902−12<902,
所以p<(910)19,
又由(2)知t∈(1,+∞),ℎ(t)=lnt−2(t−1)t+1>0,
取t=109,有ln109−2(109−1)109+1=ln109−219>0,即ln(109)19>2,也即(109)19>e2,
所以p<(910)19<1e2. x
1
3
4
5
7
y
15
20
30
40
45
使用年数x
2
3
4
5
6
7
售价y
20
12
8
6.4
4.4
3
z=lny
3.00
2.48
2.08
1.86
1.48
1.10
x
(0,13)
13
(13,2)
2
(2,+∞)
f′(x)
+
0
−
0
+
f(x)
递增
极大值
递减
极小值
递增
江西省上饶市2023-2024学年高二下学期期末教学质量检测 数学: 这是一份江西省上饶市2023-2024学年高二下学期期末教学质量检测 数学,文件包含数学pdf、数学答案pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
江西省上饶市2023-2024学年高二下学期期末教学质量检测 数学试题: 这是一份江西省上饶市2023-2024学年高二下学期期末教学质量检测 数学试题,文件包含数学pdf、数学答案pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
江西省上饶市2019-2020学年高二下学期期末教学质量测试 数学(理)试题: 这是一份江西省上饶市2019-2020学年高二下学期期末教学质量测试 数学(理)试题,共10页。试卷主要包含了 本试卷分第Ⅰ卷两部分,下列点在曲线上的是等内容,欢迎下载使用。












