




专题05 整式中的两种规律探索问题-2023-2024人教版七年级数学上学期期末复习培优专题
展开类型一、数字类规律探索
例.观察:(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,据此规律,当(x﹣1)(x5+x4+x3+x2+x+1)=0时,代数式x2019﹣1的值为 _____.
【答案】0或﹣2
【详解】解:根据题意得∶ (x﹣1)(x+1)=x2﹣1,
(x﹣1)(x2+x+1)=x3﹣1,
(x﹣1)(x3+x2+x+1)=x4﹣1,
……
∴(x﹣1)(x5+x4+x3+x2+x+1)=x6﹣1
∵(x﹣1)(x5+x4+x3+x2+x+1)=0,
∴x6﹣1=0,
解得:x=1或x=﹣1,
则x2019﹣1=0或﹣2,
故答案为:0或﹣2.
【变式训练1】a是不为1的有理数,我们把称为a的差倒数,如2的差倒数为,-1的差倒数为,已知,是差倒数,是差倒数,是差倒数,以此类推……,的值是( )
A.5B.C.D.
【答案】B
【解析】∵ , 是的差倒数,∴,
∵是的差倒数,是的差倒数,∴,∴,
根据规律可得以,,为周期进行循环,因为2021=673×3…2,所以.
故选B.
【变式训练2】有2021个数排成一行,对于任意相邻的三个数,都有中间数等于前后两数的和,如果第一个数是0,第二个数是1, 那么前6个数的和是______, 这2021个数的和是______.
【答案】0 1
【解析】由题意得:第3个数是,
第4个数是,第5个数是,第6个数是,
则前6个数的和是,
第7个数是,第8个数是,
归纳类推得:这2021个数是按循环往复的,
,且前6个数的和是0,
这2021个数的和与前5个数的和相等,即为,
故答案为:0,1.
【变式训练3】有一列数,…,那么第n个数为______.
【答案】
【详解】解:,,,
,,……
由此发现:第n个数为.
故答案为:
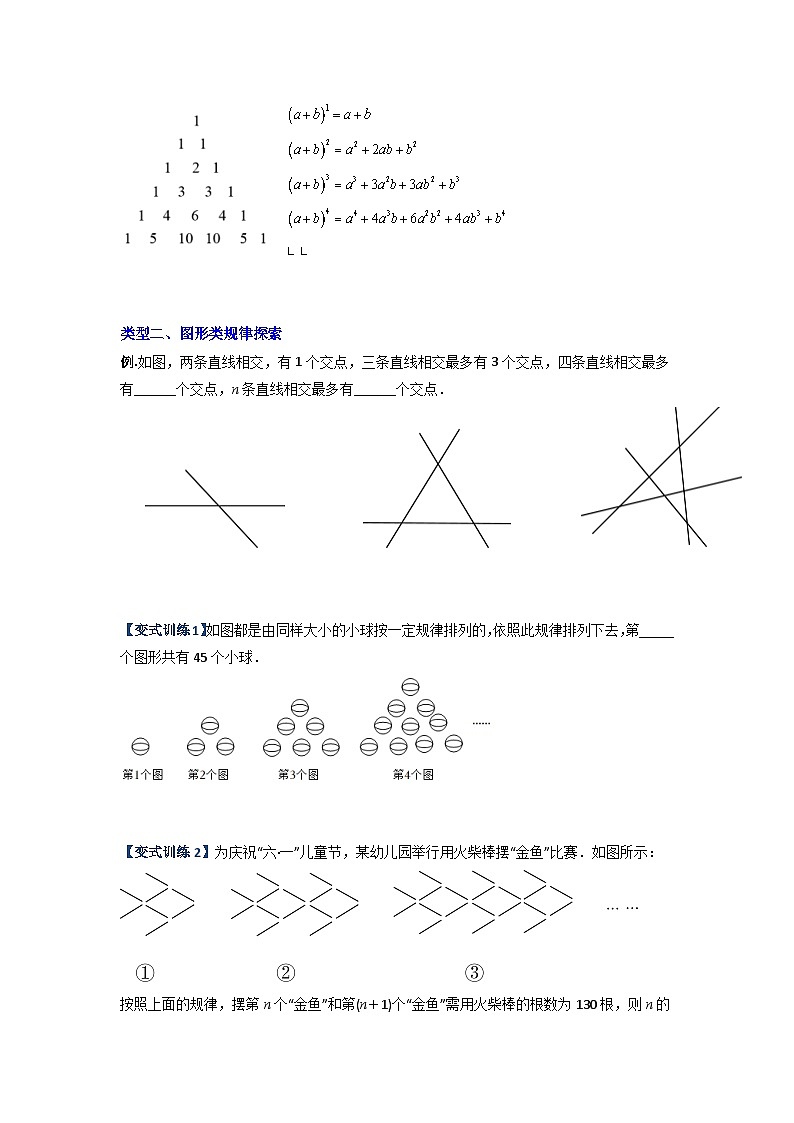
【变式训练4】杨辉三角又称贾宪三角,是二项式系数在三角形中的一种几何排列,如图,观察下面的杨辉三角:按照前面的规律,则的展开式中从左起第三项为______.
【答案】
【详解】解:根据题意,
=,
∴的展开式中从左起第三项为,
故答案为:.
类型二、图形类规律探索
例.如图,两条直线相交,有1个交点,三条直线相交最多有3个交点,四条直线相交最多有______个交点,n条直线相交最多有______个交点.
【答案】 6
【详解】解: 如图,两条直线相交最多有1个交点,即;
三条直线相交最多有3个交点,即;四条直线相交最多有6个交点,即,
五条直线相交最多有10个交点,即,……
∴n条直线两两相交,最多有个交点(n为正整数,且n≥2).
故答案为6;.
【变式训练1】如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第_____个图形共有45个小球.
【答案】9
【详解】解:第1个图中有1个小球,
第2个图中有3个小球,3=1+2,
第3个图中有6个小球,6=1+2+3,
第4个图中有10个小球,10=1+2+3+4,……
照此规律,第n个图形有1+2+3+4+…+n=n(1+n)个小球,
∴n(1+n)=45,
解得n=9或-10(舍去),
故答案为:9.
【变式训练2】为庆祝“六·一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:
按照上面的规律,摆第n个“金鱼”和第(n+1)个“金鱼”需用火柴棒的根数为130根,则n的值为______.
【答案】10
【详解】解:由题可知:第n个图形有(6n+2)根火柴棒,第(n+1)个图形有(6n+8)根火柴棒,
∵摆第n个“金鱼”和第(n+1)个“金鱼”需用火柴棒的根数为130根,
∴6n+2+6n+8=130,解得n=10.
故答案为:10.
【变式训练3】如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第10层中含有正三角形个数为___个,第层含有正三角形个数为___个.
【答案】114
【解析】根据题意分析可得:从里向外的第1层包括6个正三角形,
第2层包括18个正三角形,此后,每层都比前一层多12个,
依此递推,第10层中含有正三角形个数是6+12×9=114个,
则第n层中含有正三角形个数是6+12×(n-1)=个,
故答案为:114,.
【变式训练4】观察下列图形:
它们是按一定规律排列的,依照此规律,用6064个五角星摆出的图案应该是第_______个图形.
【答案】2021
【解析】观察发现,第1个图形五角星的个数是:1+3=4,
第2个图形五角星的个数是:1+3×2=7,
第3个图形五角星的个数是:1+3×3=10,
第4个图形五角星的个数是:1+3×4=13,⋯
第n个图形五角星的个数是:1+3•n=1+3n,
∵,
∴用6064个五角星摆出的图案应该是第2021个图形,
故答案为:2021.
课后训练
1.下列图形都是由同样大小的黑色正方形纸片组成,其中第1个图有3张黑色正方形纸片,第2个图有5张黑色正方形纸片,第3个图有7张黑色正方形纸片,…,按此规律排列下去,若第n个图中有201张黑色正方形纸片,则n的值为( )
A.99B.100C.101D.102
【答案】B
【详解】
解:观察图形知:
第一个图中有3=1+2×1个正方形,
第二个图中有5=1+2×2个正方形,
第三个图中有7=1+2×2个正方形,
…
故第n个图中有1+2×n=2n+1=201(个)正方形,
解得n=100
故选B.
2.如图,将若干颗棋子按箭头方向依次摆放,记第一颗棋子摆放的位置为第1列第1排,第二颗棋子摆放的位置为第2列第1排,第三颗棋子摆放的位置为第2列第2排……,按此规律摆放在第16列第8排的是第( )颗棋子.
A.85B.86C.87D.88
【答案】B【详解】偶数列数与排数表:
∴当n=16时,排数为:,
∴前16列共有棋子:(颗),
∴第16列第8排的棋子位次是:87-1=86.
故选B.
3.将一正方形按如图方式分成个完全相同的长方形,上、下各横排三个,中间两行各竖排若干个,则的值为( )
A.12B.16C.18D.20
【答案】C
【详解】解:设长方形的长为a,宽为b,
根据题意得,2a+2b=3a, 整理得,a=2b,
∴竖排的一行的长方形的个数为3a÷b=(3×2b)÷b=6,
∴n=3×2+6×2=6+12=18.
故选:C.
4.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则与的和是( )
A.9B.10C.11D.12
【答案】D
【详解】
解:设如图表所示:
根据题意可得:x+6+20=22+z+y,
整理得:x-y=-4+z,
x+22+n=20+z+n,20+y+m=x+z+m,整理得:x=-2+z,y=2z-22,
∴x-y=-2+z-(2z-22)=-4+z,解得:z=12,
∴x+y=3z-24=12
故选:D.
5.如图,按此规律,第6行最后一个数字是_____,第_____行最后一个数是2020.
【答案】16 674
【详解】 每一行的最后一个数字分别是1,4,7,10 ,……,
第n行的最后一个数字为:,
第6行最后一个数字为:;,解得:,
故答案为:16,674.
6.如图,每个图形中的三个数之间均具有相同的规律.根据此规律,若图形中,,则的值为________.
【答案】
【详解】解:∵1×(2+1)=3,3×(4+1)=15,5×(6+1)=35,
∴右下圆圈内的数=上方圆圈内的数×(左下圆圈内的数+1),∴M=m(n+1),
∴M=11×(12+1)=143.
故答案为:143.
7.为了求的值,可令,则,因此,所以按照以上推理计算出的值是______.
【答案】
【详解】解:令,
则,
因此,则,得:,
所以.
故答案为:.
8.今年“10.1”黄金周,适逢祖国70大庆,广西柳州赛长桌宴,民族风情浓郁,吸引了大量游客如果长桌宴按下图方式就坐(其中□代表桌子,〇代表座位),则拼接n(n为正整数)张桌子时,最多可就坐_____人.
【答案】(6n+2)
【详解】
解:根据图示知,拼1张桌子,可以坐(2+6)人.
拼2张桌子,可以坐[2+(6×2)]人.
拼3张桌子,可以坐[2+(6×3)]人.
…
拼接n(n为正整数)张桌子,可以坐(6n+2)人.
故答案是:(6n+2).
9.在日历上,我们可以发现其中某些数满足一定的规律,如图是2012年8月份的日历.我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交又相乘,再相减,例如:,,不难发现,结果都是7.
2012年8月
(1)请你再选择两个类似的部分试一试,看看是否符合这个规律;
(2)换一个月的月历试一下,是否有同样的规律?
(3)请你利用整式的运算对以上的规律加以证明.
【答案】(1),符合;(2);(3)见解析
【详解】解:(1)由题意得:
,符合;
(2);
答:换一个月的月历试一下还是同样的规律;
(3)设上边第一个数为x,则其后的数为(x+1),第二行的两个数分别为(x+7),(x+8),
根据题意,得.
10.(1)你知道下面每一个图形中各有多少个小圆圈吗?第5个图形中应该有多少个小圆圈?为什么?
(2)完成下表:
(3)如果用n表示六边形边上的小圆圈数,m表示这个六边形中小圆圈的总数,那么m和n的关系是什么?
【答案】(1)第1个图形:1个;第2个图形:7个;第3个图形:19个;第4个图形:37个;第5个图形:61个,理由见解析;(2)1,7,19,37,61;(3)
【详解】(1)观察每个图形的特点,就可以算出第1个图形的小圆圈有1个,
第2个图形的小圆圈有2+3+2=7个,
第3个图形的小圆圈有3+4+5+4+3=19个,
第4个图形的小圆圈有4+5+6+7+6+5+4=37个,
由此可推知第5个图形的小圆圈有5+6+7+8+9+8+7+6+5=61个;
(2)将(1)算出的结果填入下列表格,如下表所示,
(3)结合(1)(2)可知,与之间的函数关系为:
首尾相加得
.
11.对任意一个四位正整数m,如果m的百位数字等于个位数字与十位数字之和,m的千位数字等于十位数字的2倍与个位数字之和,那么称这个数m为“筋斗数”.例如:m=5321,满足1+2=3,2×2+1=5,所以5321是“筋斗数”.例如:m=8523,满足2+3=5,但2×2+3=7≠8,所以8523不是“筋斗数”.
(1)判断9633和2642是不是“筋斗数”,并说明理由;
(2)若m是“筋斗数”,且m与13的和能被11整除,求满足条件的所有“筋斗数”m.
【答案】(1)9633是“筋斗数”;2642不是“筋斗数”; 理由见解析
(2)m的值为9909或2110或6422
【解析】(1)解:9633是“筋斗数”,2642不是“筋斗数”,理由如下:
∵6=3+3,9=2×3+3,∴9633是“筋斗数”;
∵6=4+2,,∴2642不是“筋斗数”;
(2)设m的个位数为a,0≤a≤9,十位数为0<b≤9,且a、b为整数
∵是“筋斗数”,
∴m的百位数为a+b,千位数为2b+a;
∴m=1000(2b+a)+100(a+b)+10b+a=1100a+110b+2000b+a
∵与13的和能被11整除,
∴1100a+110b+2000b+a+13能被11整除,
∵2b+a≤9且a、b为整数,∴b≤4.5
∵1100a+110b能被11整除,
∴2000b+a+13能被11整除,
∴b=0,a=9或b=1,a=0或b=2,a=2或b=3,a=4,或b=4,a=6,
∴a+b=9,2b+a=9或a+b=1,2b+a=2或a+b=4,2b+a=6或a+b=7,2b+a=10(舍去)或a+b=10,2b+a=14(舍去),∴的值为9909或2110或6422
12.看图填空:如图,把一个面积为1的正方形等分成两个面积为的长方形,接着把面积为的长方形等分成两个面积为的长方形,再把面积为的长方形等分成面积为的长方形,如此进行下去……
(1)试利用图形揭示的规律计算:=_______.
并使用代数方法证明你的结论.
(2)请给利用图(2),再设计一个能求:的值的几何图形.
【答案】(1) ,证明见解析;(2)见解析
【解析】(1)解:①由题意可知当最后一个小长方形的面积为时 ,
的值为正方形面积减去最后一个小长方形面积,即: ,
;
②设 ,
,
,即,;
(2)如图所示,将面积为1的正方形等分成两个面积为的三角形,接着把面积为的三角形等分成两个面积为的三角形,再把面积为的三角形等分成面积为的三角形,如此进行下去,
则的值即为正方形面积减去最后一个小三角形面积:
偶数列数
排数
2
2
4
3
6
4
8
5
…
…
n
日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
边上的小圆圈数
1
2
3
4
5
每个图中小圆圈的总数
边上的小圆圈数
1
2
3
4
5
每个图中小圆圈的总数
1
7
19
37
61
专题09 几何中种动角问题的两种考法-2023-2024人教版七年级数学上学期期末复习培优专题: 这是一份专题09 几何中种动角问题的两种考法-2023-2024人教版七年级数学上学期期末复习培优专题,文件包含专题09几何中种动角问题的两种考法教师版docx、专题09几何中种动角问题的两种考法学生版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
人教版七年级数学上册同步压轴题专题05整式中的两种规律探索问题(学生版+解析): 这是一份人教版七年级数学上册同步压轴题专题05整式中的两种规律探索问题(学生版+解析),共21页。试卷主要包含了数字类规律探索,图形类规律探索等内容,欢迎下载使用。
初中数学人教版七年级上册2.1 整式一课一练: 这是一份初中数学人教版七年级上册2.1 整式一课一练,文件包含2023年初中数学7年级上册同步压轴题专题05整式中的两种规律探索问题教师版含解析docx、2023年初中数学7年级上册同步压轴题专题05整式中的两种规律探索问题学生版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。













