






高中数学湘教版(2019)选择性必修 第二册3.2 离散型随机变量及其分布列精品ppt课件
展开1.理解超几何分布的概念和应用(重点)
2.把相关问题转化为超几何分布问题进行处理(难点)
如果随机变量X只取值0或1,且其概率分布是
P(X = 1) = p, P(X = 0) = 1-p,p∈(0,1)
则称随机变量X服从两点分布,记作X~B(1,p).
一般地,在n次独立重复试验中,用X表示示事件A出现的次数,设每次试验中事件A发生的概率为p,则X的概率分布:
我们称X服从二项分布记为X~B(n,p),其分布列为:
解:从100件产品中随机抽取10件有 种等可能结果.
则依据分步计数原理有 种结果.
例7 假定一批产品共100件,其中有5件不合格品,从中随机取出10 件产品中,求取出的不合格品数X的概率分布.
假设{X = 2}表示的随机事件是“取到2件不合格品和8件合格品”,
类似地,可以求得X取其他值时对应的随机事件的概率,从而得到取出的不合格品数X的分布列为
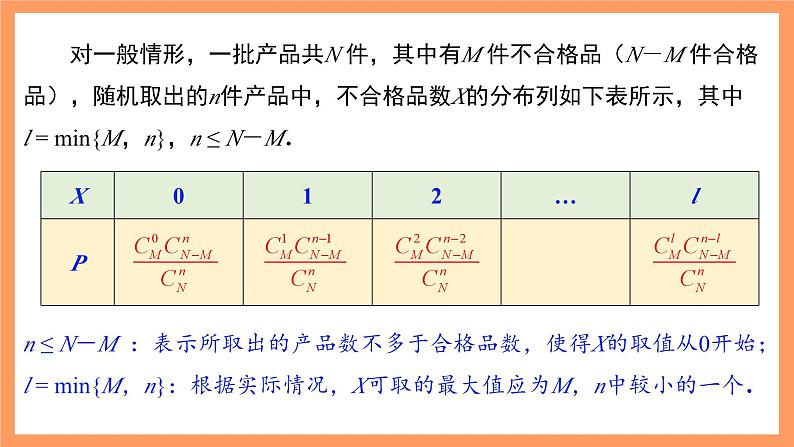
对一般情形,一批产品共N 件,其中有M 件不合格品(N-M 件合格品),随机取出的n件产品中,不合格品数X的分布列如下表所示,其中l = min{M,n},n ≤ N-M.
n ≤ N-M :表示所取出的产品数不多于合格品数,使得X的取值从0开始; l = min{M,n}:根据实际情况,X可取的最大值应为M,n中较小的一个.
对一般情形,若N 件产品中有M 件次品(M ≤ N),任取n件,其中恰有X件次品,则事件发生的概率为
其中l = min{M,n},M ≤ N ,n ≤ N-M,n,M,N∈N*.称分布列
为超几何分布列.如果随机变量X的分布列为超几何分布列,就称X服从超几何分布,记作 X~H(N,M,n).
练习1 设随机变量X~H(8,3,3),则P(X≥2) = .
解:随机变量X服从超几何分布 (X可表示为从含3件次品的8件产品中取出3件,取出的次品数.)
例8 鱼塘中只有80 条鲤鱼和20条草鱼,每条鱼被打捞的可能性相同,捞鱼者一网打捞上来4条鱼,计算:(1)其中有1条鲤鱼的概率(精确到0.001);(2)4条都是鲤鱼的概率(精确到0.001).
解:用X表示被打捞的4条鱼中鲤鱼的条数,
则 X ~ H(100,80,4).
例9 某商场为促销组织了一次幸运抽奖活动.袋中装有18个除颜色外其余均相同的小球,其中8个是红球,10个是白球.抽奖者从中一次抽出3个小球,抽到3个红球得一等奖,抽到2个红球得二等奖,抽到1个红球得三等奖,抽到0个红球不得奖.求得一等奖、二等奖和三等奖的概率(精确到0.000 1).
解:用X表示抽出的红球数,则 X ~ H(18,8,3).
记Ai=“得i等奖” (i =1,2,3),则
因此,得一等奖的概率约为0.0686,得二等奖的概率约为0.3431,得三等奖的概率约为0.4412.
练习2 某乒乓球队有9名队员,其中2名是种子选手,现挑选3名队员参加比赛,设X表示其中种子选手人数,求X的分布列.
解:X的所有取值为:0,1,2.
[拓展] 袋中有5个白球,4个黑球,从中随机抽取3次,每次取1个球,求(1)不放回抽样时,取到的黑球个数X 的分布列;(2)有放回抽样时,取到的黑球个数Y 的分布列.
(1)解:依题意,知X 服从超几何分布,即X~H(9,4,3).
[拓展] 袋中有5个白球,4个黑球,从中随机抽取3次,每次取1个球,求(1)不放回抽样时,取到的黑球个数X 的分布列;(2)有放回抽样时,取到的黑球个数Y 的分布列.
一般地,若N 件产品中有M 件次品(M ≤ N),任取n件,其中恰有X件次品,则X的概率分布为
我们称X服从超几何分布,记为 X~H(N,M,n),其分布列为:
其中l = min{M,n},M ≤ N ,n ≤ N-M,n,M,N∈N*.
P142 习题3.2 第5题 第12题
在一次购物抽奖活动中.假设某10张奖券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖.某顾客从这10张中任抽2张,求:(1)该顾客中奖的概率;(2)该顾客获得的奖品总价值X(元)的分布列.
湘教版(2019)选择性必修 第二册3.3 正态分布优秀课件ppt: 这是一份湘教版(2019)选择性必修 第二册<a href="/sx/tb_c4018237_t3/?tag_id=26" target="_blank">3.3 正态分布优秀课件ppt</a>,共1页。
高中湘教版(2019)3.2 离散型随机变量及其分布列精品ppt课件: 这是一份高中湘教版(2019)<a href="/sx/tb_c4018236_t3/?tag_id=26" target="_blank">3.2 离散型随机变量及其分布列精品ppt课件</a>,共1页。
高中数学2.4 空间向量在立体几何中的应用一等奖ppt课件: 这是一份高中数学<a href="/sx/tb_c4018232_t3/?tag_id=26" target="_blank">2.4 空间向量在立体几何中的应用一等奖ppt课件</a>,共1页。













