专题4.4 对数函数-【初升高衔接】2023年新高一数学初升高考点必杀50题（人教A版2019）（原卷版+解析版）

这是一份专题4.4 对数函数-【初升高衔接】2023年新高一数学初升高考点必杀50题（人教A版2019）（原卷版+解析版），文件包含专题44对数函数-初升高衔接2023年新高一数学初升高考点必杀50题人教A版2019原卷版docx、专题44对数函数-初升高衔接2023年新高一数学初升高考点必杀50题人教A版2019解析版docx等2份试卷配套教学资源，其中试卷共35页， 欢迎下载使用。
一、单选题
1．若，则
A．B．C．D．
2．若函数，则函数的定义域为
A．B．C．D．
3．已知函数，则函数的减区间是（ ）
A．B．C．D．
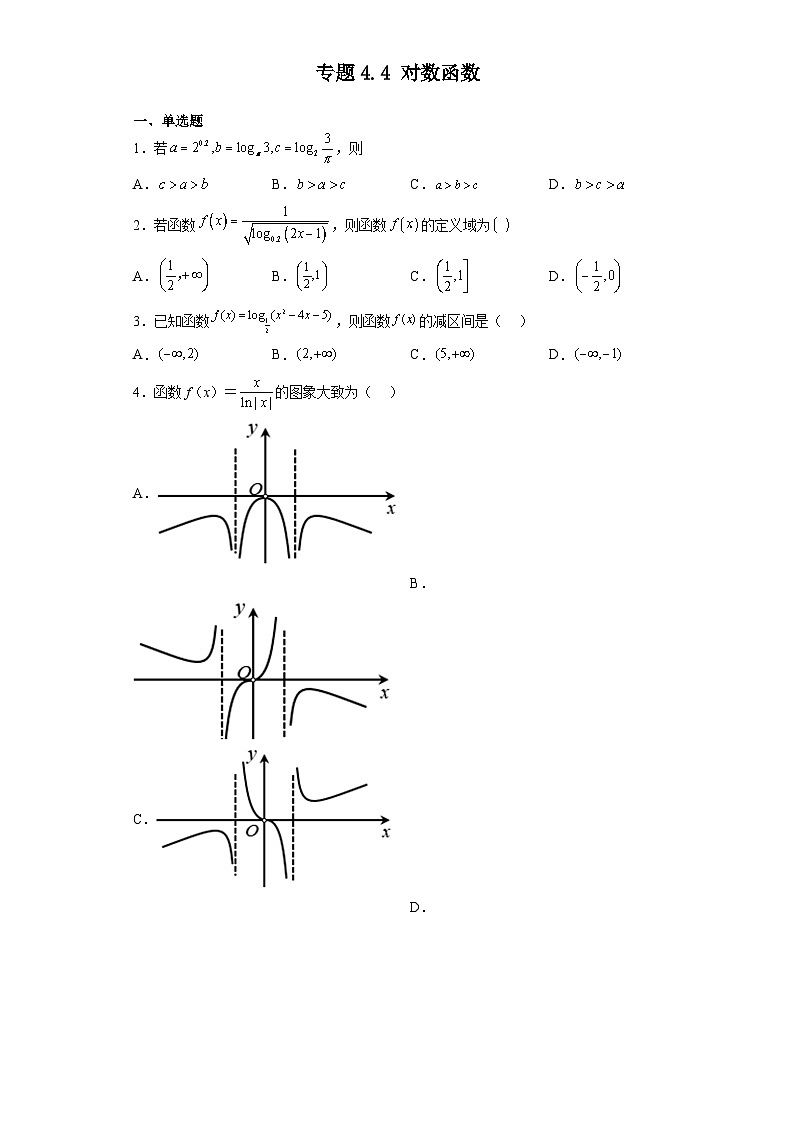
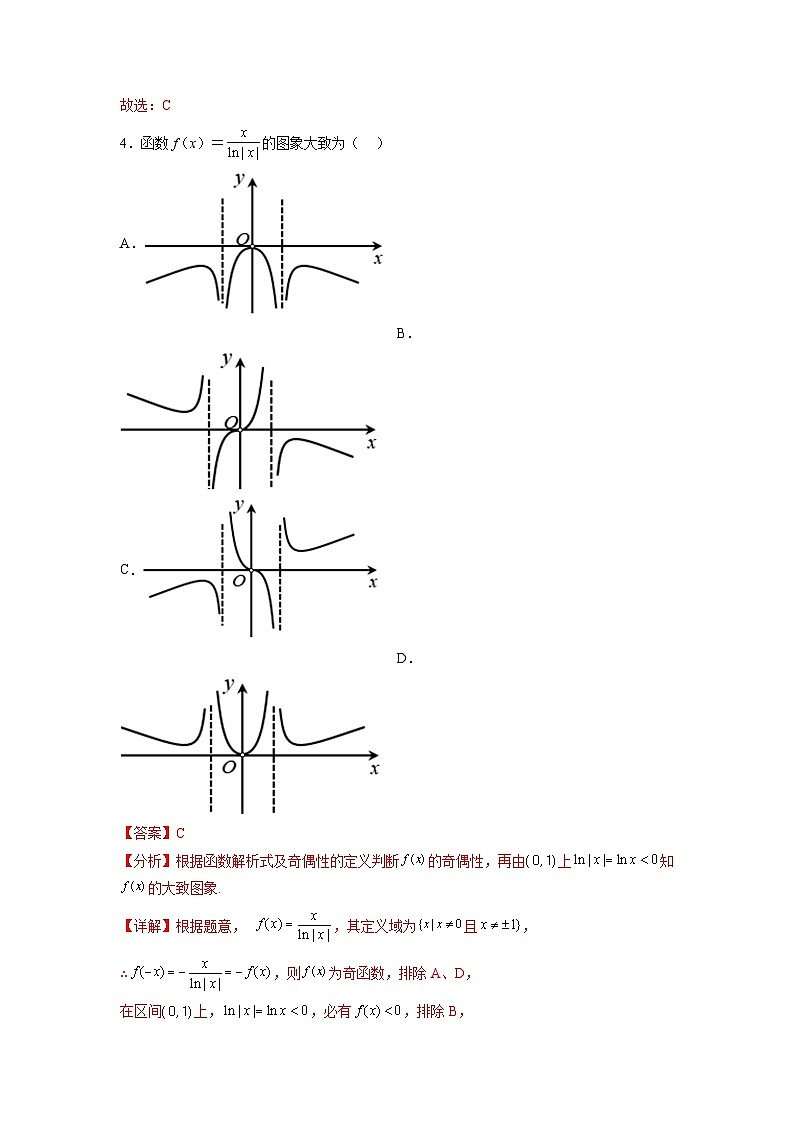
4．函数f（x）＝的图象大致为（ ）
A．B．
C．D．
5．已知，则，，的大小关系是（ ）
A．B．C．D．
6．函数的单调递减区间是（ ）
A．B．C．D．
7．设，，，则( )
A．B．C．D．
8．已知的最大值为3，则（ ）
A．9B．C．D．7
9．已知，则（ ）
A．B．
C．D．
10．已知，，，，则（ ）
A．B．C．D．
11．下列函数中，同时满足是奇函数，定义域和值域相同的函数是（ ）
A．B．C．D．
12．函数y=lgx+的定义域为（ ）
A．(2，+∞)B．(1，2]C．(0，2]D．(1，+∞)
13．已知函数，若所有点构成一个正方形区域，则（ ）
A．B．C．D．
14．已知奇函数在上是增函数，若则的大小关系是（ ）
A．B．C．D．
15．已知函数在上单调递减，则实数a的取值范围是（ ）
A．B．C．D．
16．下列关于函数的单调性及奇偶性表述正确的是
A．该函数是减函数，并且是奇函数
B．该函数是增函数，并且是偶函数
C．该函数是减函数，并且是偶函数
D．该函数的单调性及奇偶性均无法确定.
17．已知函数且，则正实数a的取值范围为（ ）
A．B．C．D．
18．设，，，则，，的大小关系为（ ）
A．B．C．D．
19．已知函数与，若存在使得，则不可能为（ ）
A．B．C．D．
20．已知实数a，b满足，，则下列判断正确的是（ ）
A．B．
C．D．
二、多选题
21．若，，则下列表达正确的是（ ）
A．B．
C．D．
22．下列四组函数中，f （x）与g（x）相等的是（ ）
A．f （x）＝ln x2，g（x）＝2ln x
B．f （x）＝x，g（x）＝（）2
C．f （x）＝x，g（x）＝
D．f （x）＝x，g（x）＝lgaax（a>0且a≠1）
23．下列函数中，既是偶函数又是区间上的增函数有（ ）
A．B．
C．D．
24．已知a＝lg23，b＝lg0.20.3，则以下结论正确的是（ ）
A．a＞1B．b＞1C．a＞bD．a+b＞2
25．已知f(x)为定义在R上的奇函数，当时，有，且当时，，下列命题正确的是（ ）
A．
B．函数在定义域上是周期为2的函数
C．直线与函数的图象有2个交点
D．函数的值域为
26．已知，则下列不等关系一定正确的是（ ）
A．B．
C．D．
27．已知，若，，则下述正确的是（ ）
A．B．
C．D．
28．若实数a，b，c满足，则（ ）
A．B．
C．D．
29．关于函数说法正确的是（ ）
A．定义域为B．图象关于轴对称
C．图象关于原点对称D．在内单调递增
30．给出以下四个结论，其中所有正确结论的序号是（ ）
A．命题“”的否定是“．”
B．若函数，则
C．“”是“函数在区间内有零点”的充要条件
D．函数（其中，且）的图象过定点
三、填空题
31．函数f（x）=+lg（2﹣x）的定义域为______
32．已知函数，则________
33．如图，点、在函数的图像上，点在函数的图像上，若为等边三角形，且直线轴，设点的坐标为，则___________.
34．设常数，函数，若的反函数的图像经过点，则________
35．函数的定义域是_____．
36．已知函数，则________．
37．已知是定义在上的奇函数，且当时，则方程的所有实根之和为________.
38．若函数在上为减函数，则的取值范围为________.
39．设，若当时有意义，则a的取值范围是_________
40．函数的单调增区间是___________.
四、解答题
41．已知.
（1）求的定义域;
（2）判断的单调性.
42．已知.
（1）求函数的定义域；
（2）判断函数的奇偶性，并加以说明；
（3）求的值.
43．利用图象判断下列函数的奇偶性：
(1)
(2)
(3)；
(4)；
(5).
44．已知函数，
（1）判断函数在上的单调性；
（2）当时，比较与的大小；
（3）若有零点，求实数m的范围．
45．已知函数．
（1）若a＞1，求f（x）的定义域；
（2）若f（x）＞0在上恒成立，求实数a的取值范围．
46．已知的定义域为．
(1)求；
(2)探究函数的单调性，并证明．
47．已知函数.
（1）求；
（2）求函数的定义域；
（3）证明函数的奇偶性.
48．已知函数（且）
(1)当时，解不等式；
(2)，，求实数的取值范围．
49．已知函数是偶函数，且.
(1)求的解析式：
(2)若不等式对恒成立，求m的取值范围.
50．已知.
(1)若，求的取值范围；
(2)若，不等式恒成立，求实数的取值范围