
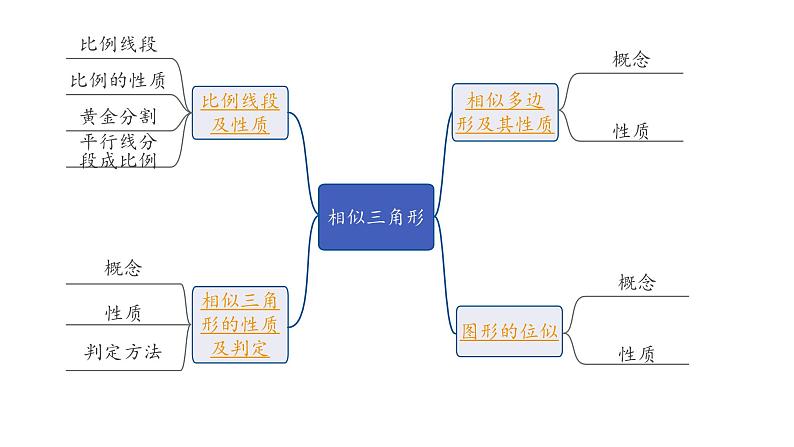




2024内蒙古中考数学一轮知识点复习 第22课时 相似三角形(含位似)(课件)
展开【对接教材】北师:九上第四章P75~P123; 人教:九下第二十七章P23~P59.
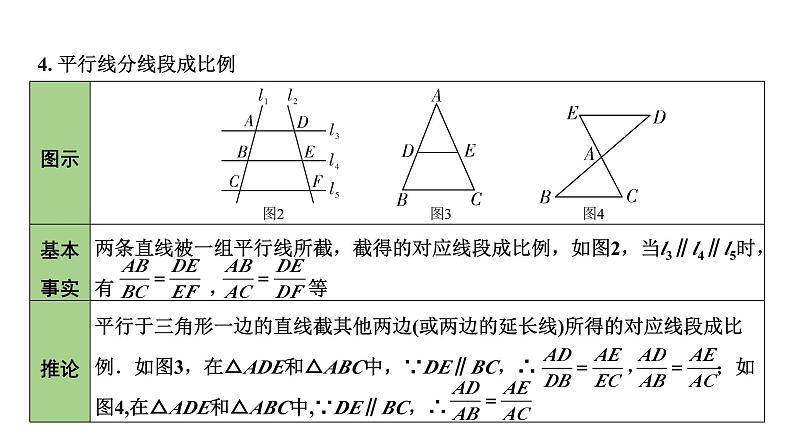
4. 平行线分线段成比例
1. 如果2x=3y(且xy≠0),则下列比例式中正确的是( )A. B. C. D.
2. 如果 = = (b+d≠0),则 =___.
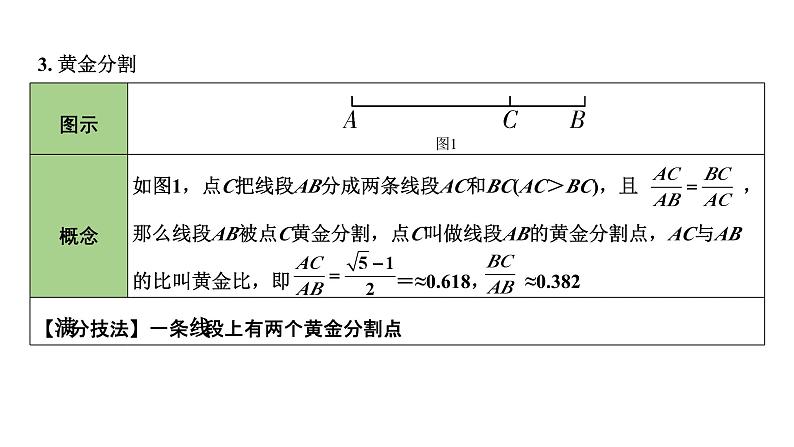
3. 一个偌大的舞台,当主持人站在黄金分割点处时,不仅看起来美观,而且音响效果也非常好,若舞台的长度为10米,那么主持人到较近的一端应为____米(精确到0.1米).
4. 如图,直线a∥b∥c,直线l1,l2与这三条平行线分别交于点A,B,C和点D,E,F.若AB∶BC=1∶2,DE=3,则EF的长为 ___.
5. 如图,已知D、E分别为AB、AC上的两点,且DE∥BC,AE=2CE,AB=6,则AD的长为___.
6. 如图,点D、E分别在△ABC的两边BA、CA的延长线上,DE∥BC,已知AE=3,AC=6,AD=2,则BD=___.
相似三角形的性质与判定
7. 如图,在△ABC中,DE∥BC,AE∶EC=2∶3,则DE∶BC=_____,△ADE的周长与△ABC的周长之比为_____,△ADE的面积与△ABC的面积之比为_______.
8. 如图,在△ABC和△ADE中,∠1=∠2,有以下四个条件,①∠B=∠D,②∠C=∠E,③ ,④ ,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件可能是________(填正确条件的序号).
9. 如图,矩形ABCD∽矩形DEFC,且面积比为4∶1,则AE∶ED的值为_____.
10. 如图,△ABC与△DEF是位似图形,位似比为2∶3,若AB=4,则DE=___.
11. 如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为________.
证明:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.1. 已知:如图,在△ABC中,DE∥BC,且DE分别交AB、AC于点D、E.求证: .【自主作答】
证明:如解图,过点E作EF∥AB,交BC于点F.
∵DE∥BC,EF∥AB,∴四边形DBFE是平行四边形,
, ,∵DE=BF,∴ ,∴ .
证明:三边成比例的两个三角形相似.2. 已知:如图,在△ABC和△A′B′C′中, .求证:△ABC∽△A′B′C′.【自主作答】
证明:如解图,在线段A′B′(或它的延长线)上截取A′D=AB,过点D作DE∥B′C′,交A′C′于点E,
∴ , ,∴DE=BC,A′E=AC,∴△A′DE≌△ABC,∴△ABC∽△A′B′C′.
1. 如图,在△ABC中,∠B=45°,点D为BC边上的一点,AD⊥AB,过点D作DE⊥AD,交AC于点E,若AB=4,DE=1,则△ABC的面积为____.
2. 如图,在△ABC中,AB=5,D,E分别是边AC和AB上的点,AD·BC= .(1)若∠AED=∠C,则DE的长为___;(2)若∠AED=∠B,则DE·AC的值为___.
3. 如图,线段AE、BD交于点C,连接AB、DE,若AC=9,CE=4,BC=CD=6,DE=3,则AB的长为____.
4. 如图,在 ABCD中,点E是边AD上一点,且AD=3ED,EC交对角线BD于点F,则 等于___.
5. (2023阜新)如图,已知每个小方格的边长均为1,则△ABC与△CDE的周长比为_____.
相似三角形的相关计算 (包头5考,呼和浩特7考,赤峰5考)
1. (2022赤峰12题3分)如图,D、E分别是△ABC边AB、AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( ) A. 1 B. 2 C. 3 D. 4
2. (2023包头17题3分)如图,在Rt△ABC中,∠ACB=90°,过点B作BD⊥CB,垂足为B,且BD=3,连接CD,与AB相交于点M,过点M作MN⊥CB,垂足为N.若AC=2,则MN的长为___.
3. (2023临沂)如图,点A,B都在格点上,若BC= ,则AC的长为( ) A. B. C. D.
4. (2023百色)如图,△ABC中,AB=AC,∠B=72°.∠ACB的平分线CD交AB于点D,则点D是线段AB的黄金分割点.若AC=2,则BD=______.
5. (2023烟台)《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE =0.4米,那么CD为___米.
6. (2023黄冈)如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.(1)求证:△ABC∽△DEC;
(1)证明:∵∠BCE=∠ACD,∴∠BCE+∠ACE=∠ACD+∠ACE,即∠ACB=∠DCE.又∵∠A=∠D,∴△ABC∽△DEC;
(2)若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.
7. (2023广元节选)如图①,在△ABC中,∠ACB=90°,AC=BC,点D是AB边上一点(含端点A、B),过点B作BE垂直于射线CD,垂足为E,点F在射线CD上,且EF=BE,连接AF、BF.(1)求证:△ABF∽△CBE;
又∵EF=BE,∴FB= EB,∠FBE=∠EFB=45°.∴∠ABE+∠FBE=∠ABC+∠ABE,即∠ABF=∠CBE .又∵ ,∴△ABF∽△CBE;
(2)如图②,连接AE,点P、M、N分别为线段AC、AE、EF的中点,连接PM、MN、PN.求∠PMN的度数及 的值.
2024内蒙古中考数学一轮知识点复习 第25课时 矩形(课件): 这是一份2024内蒙古中考数学一轮知识点复习 第25课时 矩形(课件),共21页。PPT课件主要包含了矩形的性质与判定,相等且互相平分,直角或90°,回归教材,例1题图,例2题图①,面积相等的等腰三角形,例2题图②,例3题图,例3题图③等内容,欢迎下载使用。
2024内蒙古中考数学一轮知识点复习 第5课时 分 式(课件): 这是一份2024内蒙古中考数学一轮知识点复习 第5课时 分 式(课件),共28页。PPT课件主要包含了考点精讲,分式的相关概念及性质,B≠0,A=0且B≠0,不等于零,x≠3,x-5,分式的运算,乘除运算,加减运算等内容,欢迎下载使用。
2024贵州中考数学一轮知识点复习 第33讲 图形的平移、旋转与位似(课件): 这是一份2024贵州中考数学一轮知识点复习 第33讲 图形的平移、旋转与位似(课件),共22页。PPT课件主要包含了第1题图,第2题图,第3题图,第4题图,第5题图,网格中的图形变换,第7题图,第8题图,考点精讲,图形的平移等内容,欢迎下载使用。












