

苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.3勾股定理的应用】(原卷版+解析)
展开3.3 勾股定理的应用
一.选择题
1.(2022秋•即墨区校级月考)如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
A.7.5尺B.8尺C.8.5尺D.9尺
2.(2022春•长汀县期中)为预防新冠疫情,民生大院入口的正上方A处装有红外线激光测温仪(如图所示),测温仪离地面的距离AB=2.4米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为1.8米的市民CD正对门缓慢走到离门0.8米的地方时(即测温仪自动显示体温),则人头顶高测温仪的距离AD等于( )
A.1.5米B.1.25米C.1.2米D.1.0米
3.(2021秋•开江县期末)如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条长16的直吸管露在罐外部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.4≤a≤5B.3≤a≤4C.2≤a≤3D.1≤a≤2
4.(2021秋•新吴区期末)如图,长为16cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C向上拉升6cm至D点,则橡皮筋被拉长了( )
A.4cmB.5cmC.6cmD.7cm
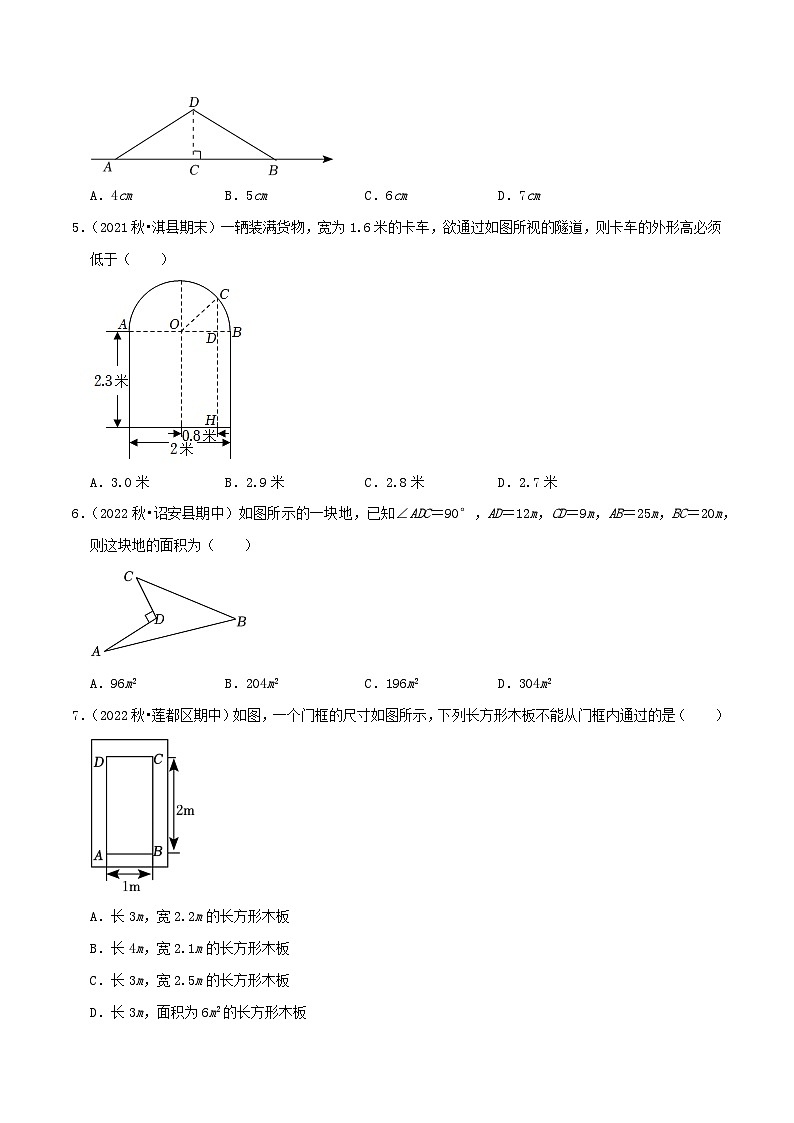
5.(2021秋•淇县期末)一辆装满货物,宽为1.6米的卡车,欲通过如图所视的隧道,则卡车的外形高必须低于( )
A.3.0米B.2.9米C.2.8米D.2.7米
6.(2022秋•诏安县期中)如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )
A.96m2B.204m2C.196m2D.304m2
7.(2022秋•莲都区期中)如图,一个门框的尺寸如图所示,下列长方形木板不能从门框内通过的是( )
A.长3m,宽2.2m的长方形木板
B.长4m,宽2.1m的长方形木板
C.长3m,宽2.5m的长方形木板
D.长3m,面积为6m2的长方形木板
8.(2022秋•锦江区校级期中)如图所示,15只空油桶(每只油桶底面直径均为60cm)堆在一起,要给它盖一个遮雨棚,遮雨棚的高度至少为( )
A.300.B.C.D.
9.(2021秋•建邺区期末)如图,将风筝放至高30m,牵引线与水平面夹角约为45°的高空中,则牵引线AB的长度所在范围最有可能是( )
A.36m至38mB.38m至40mC.40m至42mD.42m至44m
10.(2022春•沂水县期中)如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如①图所示,人只要移至该门口4m及4m以内时,门铃就会自动发出语音“欢迎光临”,如②图所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则该生头顶C到门铃A的距离为( )
A.3米B.4米C.5米D.6米
二.填空题
11.(2022春•枣阳市期末)我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐,问葭长几何.”(丈、尺是长度单位,1丈=10尺)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.这根芦苇的长度是 尺.
12.(2021秋•惠山区校级期末)如图,《九章算术》中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何.译文:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长3尺),牵着绳索退行,在距木柱底部8尺(BC=8)处时而绳索用尽.则木柱长为 尺.
13.(2021秋•仓山区校级期末)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A′D为1.5米,则小巷的宽为 米.
14.(2021秋•金台区期末)小明想测量旗杆的高度,他先将升旗的绳子拉到旗杆底端,并在绳子对应旗杆底端的位置上打了一个结,然后将绳子拉到离旗杆底部4m处,绳头恰好接触到地面,他发现此时绳头距打结处约1m,小明计算出旗杆的高度为 m.
15.(2022秋•新吴区期中)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛的意思)一尺,不合二寸,问门广几何?题目的大致意思是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都是1尺(1尺=10寸),则AB的长是几寸?若设图中单扇门的宽AD=x寸,则可列方程为: .
16.(2022秋•惠山区期中)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.在《九章算术》中的勾股卷中有这样一道题:今有竹高一丈,末折抵底,去本三尺.问折者高几何?意思为:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹稍恰好抵地,抵地处B离远处竹子C的距离BC为3尺,则折断后的竹子AC= 尺.(注:1丈=10尺.)
17.(2022春•瑞安市期中)如图1是重型卡车的立体图,图2是一个装有货物的长方体形状的木箱沿着坡面从重型卡车车上卸载的平面示意图.已知重型卡车车身高度AC=4m,卡车卸货时后面支架AB弯折落在地面A',经过测量A′C=2m.现有木箱长ED=5m,高EF=2.5m,宽小于卡车车身的宽度,当木箱底部顶点G与坡面底部点A′重合时,则木箱上部顶点E到地面A'C的距离为 m.
18.(2022春•西工区期中)如图是一个零件的示意图,测量AB=4cm,BC=3cm,CD=12cm,AD=13cm,若∠ABC=90°,则∠ACD= °.
19.(2021秋•建邺区期末)如图,一根长为18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙刷露在杯子外面的长度hcm,则h的取值范围是 .
20.(2022春•公安县期末)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆5m处,发现此时绳子末端距离地面1m,则旗杆的高度为 m.(滑轮上方的部分忽略不计)
三.解答题
21.(2022秋•镇江期中)国庆节前,学校开展艺术节活动,小明站在距离教学楼(CD)35米的A处,操控一架无人机进行摄像,已知无人机在D点处显示的高度为距离地面30米,随后无人机沿直线匀速飞行到点E处悬停拍摄,此时显示距离地面10米,随后又沿着直线飞行到点B处悬停拍摄,此时正好位于小明的头项正上方(AB∥CD),且显示距离地面25米,已知无人机从点D匀速飞行到点E所用时间与它从点E匀速飞行到点B所用时间相同,你能求出无人机从点D到点E再到点B一共飞行了多少米吗?请写出相应计算过程.
22.(2022秋•太原期中)为庆祝中华人民共和国成立73周年,喜迎党的二十大胜利召开,学校组织了“献礼二十大”小制作展示活动.小彬计划制作一架飞机模型,如图的四边形材料是飞机垂直尾翼的雏形.小彬测量发现AB=25cm,BC=18cm,AD=7cm,CD=30cm.根据设计要求,还需保证AD∥BC.由于手头工具有限,小彬只能测得BD=24cm.根据以上数据,请你判断该材料是否符合设计要求,并说明理由.
23.(2022秋•渠县校级期中)如图,OM,ON是两条公路,∠O=30°,沿公路OM方向离点O160米的点A处有一所学校,当重型运输卡车沿道路ON方向行驶时,在以重型运输卡车所在的点P为圆心,100m长为半径的圆形区域内都会受到卡车噪声的影响,且点P与点A的距离越近噪声影响越大.假设重型运输卡车沿着道路ON方向行驶的速度为18千米/小时.
(1)求对学校的噪声影响最大时,卡车与学校之间的距离;(直角三角形中30°锐角所对的直角边等于斜边的一半).
(2)求卡车沿道路ON方向行驶一次给学校带来噪声影响的时间.
24.(2022秋•沙坪坝区校级期中)如图是一个滑梯示意图,若将滑梯BD水平放置,则刚好与DE一样长,已知滑梯的高度CE为3米,BC为1米.
(1)求滑道BD的长度;
(2)若把滑梯BD改成滑梯BF,使∠BFA=60°,则求出DF的长.(精确到0.1米,参考数据:≈1.732)
25.(2022秋•罗湖区校级期中)有一个小朋友拿一根竹竿要通过一个长方形的门,若把竹竿竖着放比门高出1尺,斜着放恰好等于门的对角线长,已知门宽为4尺,求竹竿高.
解:设竹竿高为x尺,则门高 尺.(用x的代数式表示)
根据题意,可列关于x的方程: .
解得:x= .
答:
26.(2022•成武县校级开学)如图,一根直立的旗杆高8m,因刮大风旗杆从点C处折断,顶部B着地且离旗杆底部A4m.
(1)求旗杆距地面多高处折断;
(2)工人在修复的过程中,发现在折断点C的下方1.25m的点D处,有一明显裂痕,若下次大风将旗杆从点D处吹断,则距离旗杆底部周围多大范围内有被砸伤的危险?
27.(2022春•开封期末)如图,某块四边形的实验田ABCD,经测量可知∠B=90°,AB=24米,BC=7米,CD=15米,AD=20米.
(1)判断∠D是否为直角,并说明理由.
(2)求四边形ABCD的面积.
28.(2022春•綦江区期末)今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)求∠ACB的度数;
(2)海港C受台风影响吗?为什么?
(3)若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?
29.(2022秋•沙县期中)由于大风,山坡上的一棵树甲被从A点处拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部C处,已知AB=4米,BC=13米,两棵树的水平距离为12米,求这棵树原来的高度.
2022-2023学年八年级数学上册考点必刷练精编讲义(苏科版)提高
第3章《勾股定理》
3.3 勾股定理的应用
一.选择题
1.(2022秋•即墨区校级月考)如图,有一个水池,水面是边长为8尺的正方形,在水池中央有一根芦苇,它高出水面1尺,如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,这根芦苇的长度是( )
A.7.5尺B.8尺C.8.5尺D.9尺
解:设芦苇的长度为x尺,则AB为(x﹣1)尺,
根据勾股定理得:(x﹣1)2+()2=x2,
解得:x=8.5,
芦苇的长度=8.5尺,
故选:C.
2.(2022春•长汀县期中)为预防新冠疫情,民生大院入口的正上方A处装有红外线激光测温仪(如图所示),测温仪离地面的距离AB=2.4米,当人体进入感应范围内时,测温仪就会自动测温并报告人体体温.当身高为1.8米的市民CD正对门缓慢走到离门0.8米的地方时(即测温仪自动显示体温),则人头顶高测温仪的距离AD等于( )
A.1.5米B.1.25米C.1.2米D.1.0米
解:如图,过点D作DE⊥AB于点E,
∵AB=2.4米,BE=CD=1.8米,ED=BC=0.8米,
∴AE=AB﹣BE=2.4﹣1.8=0.6(米).
在Rt△ADE中,由勾股定理得到:
AD===1.0(米),
故选:D.
3.(2021秋•开江县期末)如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条长16的直吸管露在罐外部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A.4≤a≤5B.3≤a≤4C.2≤a≤3D.1≤a≤2
解:设b是圆柱形的高,
当吸管底部在地面圆心时吸管在罐内部分b最短,
此时b就是圆柱形的高,
即b=12;
∴a=16﹣12=4,
当吸管底部在饮料罐的壁底时吸管在罐内部分b最长,
b==13,
∴此时a=3,
所以3≤a≤4.
故选:B.
4.(2021秋•新吴区期末)如图,长为16cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C向上拉升6cm至D点,则橡皮筋被拉长了( )
A.4cmB.5cmC.6cmD.7cm
解:Rt△ACD中,AC=AB=8cm,CD=6cm;
根据勾股定理,得:AD==10(cm);
∴AD+BD﹣AB=2AD﹣AB=20﹣16=4(cm);
故橡皮筋被拉长了4cm.
故选:A.
5.(2021秋•淇县期末)一辆装满货物,宽为1.6米的卡车,欲通过如图所视的隧道,则卡车的外形高必须低于( )
A.3.0米B.2.9米C.2.8米D.2.7米
解:∵车宽1.6米,
∴欲通过如图的隧道,只要比较距隧道中线0.8米处的高度与车高.
在Rt△OCD中,由勾股定理可得:
CD===0.6(米),
∴CH=CD+DH=0.6+2.3=2.9(米),
∴卡车的外形高必须低于2.9米.
故选:B.
6.(2022秋•诏安县期中)如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )
A.96m2B.204m2C.196m2D.304m2
解:如图,连接AC.
∵AD=12m,CD=9m,∠ADC=90°,
∴AC===15(m),
又∵AB=25m,BC=20m,
∴AC2+BC2=152+202=252=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴这块地的面积=△ABC的面积﹣△ACD的面积=×15×20﹣×9×12=96(m2).
故选:A.
7.(2022秋•莲都区期中)如图,一个门框的尺寸如图所示,下列长方形木板不能从门框内通过的是( )
A.长3m,宽2.2m的长方形木板
B.长4m,宽2.1m的长方形木板
C.长3m,宽2.5m的长方形木板
D.长3m,面积为6m2的长方形木板
解:如图,连接AC,
∵四边形ABCD是长方形,
∴∠ABC=90°,
根据勾股定理得:AC===≈2.236(m),
四个选项中只有2.5>2.236,
∴长3m,宽2.5m的长方形木板不能从门框内通过,
故选:C.
8.(2022秋•锦江区校级期中)如图所示,15只空油桶(每只油桶底面直径均为60cm)堆在一起,要给它盖一个遮雨棚,遮雨棚的高度至少为( )
A.300.B.C.D.
解:取三个角处的三个油桶的圆心,连接组成一个等边三角形,
它的边长是4×60=240cm,
这个等边三角形的高是=120cm,雨棚起码高是:(120+60)cm.
故选:D.
9.(2021秋•建邺区期末)如图,将风筝放至高30m,牵引线与水平面夹角约为45°的高空中,则牵引线AB的长度所在范围最有可能是( )
A.36m至38mB.38m至40mC.40m至42mD.42m至44m
解:如图,过B作BC⊥水平面于C,
∵∠BAC=45°,
∴△ABC是等腰直角三角形,
∴AC=BC=30m,
∴AB===30≈42.42(m),
故选:D.
10.(2022春•沂水县期中)如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如①图所示,人只要移至该门口4m及4m以内时,门铃就会自动发出语音“欢迎光临”,如②图所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则该生头顶C到门铃A的距离为( )
A.3米B.4米C.5米D.6米
解:由题意可知.BE=CD=1.5m,AE=AB﹣BE=4.5﹣1.5=3m,CE=4m,
由勾股定理得AC===5(m),
故离门5米远的地方,门铃恰好自动响起.
故选:C.
二.填空题
11.(2022春•枣阳市期末)我国古代数学著作《九章算术》中记载了一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺,引葭赴岸,适与岸齐,问葭长几何.”(丈、尺是长度单位,1丈=10尺)其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.这根芦苇的长度是 13 尺.
解:设水深为x尺,则芦苇长为(x+1)尺,
根据勾股定理得:x2+()2=(x+1)2,
解得:x=12,
芦苇的长度=x+1=12+1=13(尺),
答:芦苇长13尺.
故答案为:13.
12.(2021秋•惠山区校级期末)如图,《九章算术》中记载:今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何.译文:今有一竖直着的木柱,在木柱的上端系有绳索,绳索从木柱的上端顺木柱下垂后堆在地面的部分有三尺(绳索比木柱长3尺),牵着绳索退行,在距木柱底部8尺(BC=8)处时而绳索用尽.则木柱长为 尺.
解:设木柱长为x尺,根据题意得:
AB2+BC2=AC2,
则x2+82=(x+3)2,
解得:x=,
答:木柱长为尺.
故答案为:.
13.(2021秋•仓山区校级期末)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A′D为1.5米,则小巷的宽为 2.7 米.
解:在Rt△ABC中,
AB===2.5(米),
∴A′B=2.5米,
在Rt△A′BD中,
BD===2(米),
∴BC+BD=2+0.7=2.7(米),
答:小巷的宽为2.7米,
故答案为:2.7.
14.(2021秋•金台区期末)小明想测量旗杆的高度,他先将升旗的绳子拉到旗杆底端,并在绳子对应旗杆底端的位置上打了一个结,然后将绳子拉到离旗杆底部4m处,绳头恰好接触到地面,他发现此时绳头距打结处约1m,小明计算出旗杆的高度为 7.5 m.
解:设旗杆的高为xm,则绳子长为(x+1)m,
由勾股定理得,(x+1)2=x2+42,
解得,x=7.5.
答:旗杆的高度是7.5m,
故答案为:7.5.
15.(2022秋•新吴区期中)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(门槛的意思)一尺,不合二寸,问门广几何?题目的大致意思是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都是1尺(1尺=10寸),则AB的长是几寸?若设图中单扇门的宽AD=x寸,则可列方程为: (x﹣1)2+102=x2 .
解:取AB的中点O,过D作DE⊥AB于E,如图2所示:
由题意得:OA=OB=AD=BC,
设OA=OB=AD=BC=x寸,
则AB=2x(寸),DE=10寸,OE=CD=1寸,
∴AE=(x﹣1)寸,
在Rt△ADE中,
AE2+DE2=AD2,即(x﹣1)2+102=x2,
故答案为:(x﹣1)2+102=x2.
16.(2022秋•惠山区期中)《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.在《九章算术》中的勾股卷中有这样一道题:今有竹高一丈,末折抵底,去本三尺.问折者高几何?意思为:一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹稍恰好抵地,抵地处B离远处竹子C的距离BC为3尺,则折断后的竹子AC= 尺.(注:1丈=10尺.)
解:设折断后的竹子AC为x尺,则斜边AB为(10﹣x)尺,
在Rt△ABC中,根据勾股定理得:x2+32=(10﹣x)2,
解得:x=,
故答案为:.
17.(2022春•瑞安市期中)如图1是重型卡车的立体图,图2是一个装有货物的长方体形状的木箱沿着坡面从重型卡车车上卸载的平面示意图.已知重型卡车车身高度AC=4m,卡车卸货时后面支架AB弯折落在地面A',经过测量A′C=2m.现有木箱长ED=5m,高EF=2.5m,宽小于卡车车身的宽度,当木箱底部顶点G与坡面底部点A′重合时,则木箱上部顶点E到地面A'C的距离为 5 m.
解:如图2,作EJ⊥A′C于点J,FH⊥A′C于点H,FI⊥FJ于点I,
∵AC⊥A′C,GB⊥AC,
∴FH∥EJ∥AB,FI∥BG∥A′C,
∴IJ=FH,GH=BC,∠EIF=∠BGF=∠CHG=∠A′CB=∠90°,∠FBG=∠BA′C,
设A′B=AB=x,
∵A′C2+BC2=A′B2,且AC=4m,A′C=2m,
∴22+(4﹣x)2=x2,
解得x=2.5,
∴A′B=2.5m,GH=BC=4﹣2.5=1.5(m),
∵四边形A′DEF是长方形,ED=5m,EF=2.5m,
∴A′F=ED=5m,
∴EF=BF=A′B=2.5m,
在△BGF和△A′CB中,
,
∴△BGF≌△A′CB(ASA),
∴FG=BC=1.5m,BG=A′C=2m,
∴IJ=FH=FG+GH=1.5+1.5=3(m),
∵∠BFE=90°,∠IFH=180°﹣∠CHG=90°,
∴∠EFI=∠BFG=90°﹣∠BFI,
在△EIF和△BGF中,
,
∴△EIF≌△BGF(AAS),
∴EI=BG=2m,
∴EJ=EI+IJ=2+3=5(m),
∴木箱上部顶点E到地面A'C的距离为5m,
故答案为:5.
18.(2022春•西工区期中)如图是一个零件的示意图,测量AB=4cm,BC=3cm,CD=12cm,AD=13cm,若∠ABC=90°,则∠ACD= 90 °.
解:在Rt△ABC中,AB=4cm,BC=3cm,∠ABC=90°,
∴AC==5(cm),
在△ACD中,AD=13cm,CD=12cm,AC=5cm,
∴AD2=169,CD2+AC2=169,
∴AD2=CD2+AC2,
∴△ACD是直角三角形,
∴∠ACD=90°.
故答案为:90.
19.(2021秋•建邺区期末)如图,一根长为18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中,牙刷露在杯子外面的长度hcm,则h的取值范围是 5≤h≤6 .
解:当牙刷与杯底垂直时h最大,h最大=18﹣12=6(cm).
当牙刷与杯底及杯高构成直角三角形时h最小,
如图,此时,AB===13(cm),
则h=18﹣13=5(cm).
∴h的取值范围是5≤h≤6.
故答案为:5≤h≤6.
20.(2022春•公安县期末)如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆5m处,发现此时绳子末端距离地面1m,则旗杆的高度为 13 m.(滑轮上方的部分忽略不计)
解:设旗杆高度为x米,则AC=x米,AD=(x﹣1)m,BC=5米,
在Rt△ADC中,AD2+DC2=AC2,即(x﹣1)2+52=x2,
解得x=13,
即旗杆的高度为13米.
故答案为:13.
三.解答题
21.(2022秋•镇江期中)国庆节前,学校开展艺术节活动,小明站在距离教学楼(CD)35米的A处,操控一架无人机进行摄像,已知无人机在D点处显示的高度为距离地面30米,随后无人机沿直线匀速飞行到点E处悬停拍摄,此时显示距离地面10米,随后又沿着直线飞行到点B处悬停拍摄,此时正好位于小明的头项正上方(AB∥CD),且显示距离地面25米,已知无人机从点D匀速飞行到点E所用时间与它从点E匀速飞行到点B所用时间相同,你能求出无人机从点D到点E再到点B一共飞行了多少米吗?请写出相应计算过程.
解:过E作MN⊥AB于M,交CD于N,
由题意得AB=25米,CD=30米,AC=35米,AB∥CD,AB⊥AC,EF⊥AC,CD⊥AC,BE=DE,
∴MN⊥CD,
∴四边形AMEF,四边形EFCN,四边形ACNM是矩形,
∴MN=AC=35米,BM=15米,DN=20米,EN=(35﹣EM)米,
在Rt△ABM中,BE2=BM2+EM2,
在Rt△DEN中,DE2=DN2+EN2,
∴BM2+EM2=DN2+EN2,
∴152+EM2=202+(35﹣EM)2,
解得EM=20米,
∴BE==25(米),
∴BE+DE=50米.
答:无人机从点D到点E再到点B一共飞行了50米.
22.(2022秋•太原期中)为庆祝中华人民共和国成立73周年,喜迎党的二十大胜利召开,学校组织了“献礼二十大”小制作展示活动.小彬计划制作一架飞机模型,如图的四边形材料是飞机垂直尾翼的雏形.小彬测量发现AB=25cm,BC=18cm,AD=7cm,CD=30cm.根据设计要求,还需保证AD∥BC.由于手头工具有限,小彬只能测得BD=24cm.根据以上数据,请你判断该材料是否符合设计要求,并说明理由.
解:该材料符合设计要求,
理由如下:
在△ABD中,AD2+BD2=72+242=625,AB2=252=625,
∴AD2+BD2=AB2,
∴∠ADB=90°,
在△BCD中,BC2+BD2=182+242=900,CD2=302=900,
∴BC2+BD2=CD2,
∴∠CBD=90°,
∴∠ADB=∠CBD,
∴AD∥BC,
∴该材料符合设计要求.
23.(2022秋•渠县校级期中)如图,OM,ON是两条公路,∠O=30°,沿公路OM方向离点O160米的点A处有一所学校,当重型运输卡车沿道路ON方向行驶时,在以重型运输卡车所在的点P为圆心,100m长为半径的圆形区域内都会受到卡车噪声的影响,且点P与点A的距离越近噪声影响越大.假设重型运输卡车沿着道路ON方向行驶的速度为18千米/小时.
(1)求对学校的噪声影响最大时,卡车与学校之间的距离;(直角三角形中30°锐角所对的直角边等于斜边的一半).
(2)求卡车沿道路ON方向行驶一次给学校带来噪声影响的时间.
解:(1)过点A作AH⊥ON于H,
∵∠O=30°,OA=160米,
∴AH=OA=80米,
∴卡车P对学校A的噪声影响最大时,卡车P与学校A的距离为80米;
(2)当AC=AN=100米时,则卡车在CD段对学校A有影响,
由(1)知AH=80米,
∴CH=60(米),
∴CN=2CH=120(米),
∴t=120÷=24(秒),
∴卡车P沿道路ON方向行驶一次,它给学校A带来噪声影响的总时间为24秒.
24.(2022秋•沙坪坝区校级期中)如图是一个滑梯示意图,若将滑梯BD水平放置,则刚好与DE一样长,已知滑梯的高度CE为3米,BC为1米.
(1)求滑道BD的长度;
(2)若把滑梯BD改成滑梯BF,使∠BFA=60°,则求出DF的长.(精确到0.1米,参考数据:≈1.732)
解:(1)设BD的长为x米,则DE=x米,AD=DE﹣AE=(x﹣1)米,
由题意得:∠BAD=90°,AB=CE=3米,
在Rt△ABD中,由勾股定理得:x2=32+(x﹣1)2,
解得:x=5,
答:滑道BD的长为5米;
(2)∵∠BFA=60°,
∴∠ABF=90°﹣∠BFA=30°,
∴BF=2AF,
设AF=a米,则BF=2a米,
∴AB===a(米),
∴a=3,
解得:a=,
∴AF=米,
由(1)可知,AD=4米,
∴DF=AD﹣AF=4﹣≈2.3(米),
答:DF的长约为2.3米.
25.(2022秋•罗湖区校级期中)有一个小朋友拿一根竹竿要通过一个长方形的门,若把竹竿竖着放比门高出1尺,斜着放恰好等于门的对角线长,已知门宽为4尺,求竹竿高.
解:设竹竿高为x尺,则门高 (x﹣1) 尺.(用x的代数式表示)
根据题意,可列关于x的方程: (x﹣1)2+42=x2 .
解得:x= 8.5 .
答:
解:设竹竿高为x尺,则门高(x﹣1)尺.
根据题意,得:(x﹣1)2+42=x2,
解得:x=8.5,
答:竹竿高为8.5尺.
故答案为:(x﹣1),(x﹣1)2+42=x2,8.5.
26.(2022•成武县校级开学)如图,一根直立的旗杆高8m,因刮大风旗杆从点C处折断,顶部B着地且离旗杆底部A4m.
(1)求旗杆距地面多高处折断;
(2)工人在修复的过程中,发现在折断点C的下方1.25m的点D处,有一明显裂痕,若下次大风将旗杆从点D处吹断,则距离旗杆底部周围多大范围内有被砸伤的危险?
解:(1)由题意可知:AC+BC=8米,
∵∠A=90°,
∴AB2+AC2=BC2,
又∵AB=4米,
∴AC=3米,BC=5米,
故旗杆距地面3米处折断;
(2)如图,
∵D点距地面AD=3﹣1.25=1.75米,
∴B'D=8﹣1.75=6.25米,
∴AB′=米,
∴距离杆脚周围6米大范围内有被砸伤的危险.
27.(2022春•开封期末)如图,某块四边形的实验田ABCD,经测量可知∠B=90°,AB=24米,BC=7米,CD=15米,AD=20米.
(1)判断∠D是否为直角,并说明理由.
(2)求四边形ABCD的面积.
解:(1)∠D是直角,
理由:连接AC,
∵∠B=90°,AB=24米,BC=7米,
∴AC=(米),
∵CD=15米,AD=20米,
∴CD2+AD2=AC2,
∴△ACD为直角三角形,∠D=90°;
(2)S四边形ABCD=S△ABC+S△ACD
=
=
=234.
28.(2022春•綦江区期末)今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)求∠ACB的度数;
(2)海港C受台风影响吗?为什么?
(3)若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?
解:(1)∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
(2)海港C受台风影响,理由:过点C作CD⊥AB于D,
∵△ABC是直角三角形,
∴AC×BC=CD×AB,
∴300×400=500×CD,
∴CD=240(km),
∵以台风中心为圆心周围260km以内为受影响区域,
∴海港C受台风影响;
(3)当EC=260km,FC=260km时,正好影响C港口,
∵ED=(km),
∴EF=2ED=200km,
∵台风的速度为28千米/小时,
∴200÷28=(小时).
答:台风影响该海港持续的时间为小时.
29.(2022秋•沙县期中)由于大风,山坡上的一棵树甲被从A点处拦腰折断,如图所示,其树顶端恰好落在另一棵树乙的根部C处,已知AB=4米,BC=13米,两棵树的水平距离为12米,求这棵树原来的高度.
解:如图所示:延长AB,过点C作CD⊥AB延长线于点D,
由题意可得:BC=13m,DC=12m,
故BD==5(m),
即AD=9m,
则AC===15(m),
故AC+AB=15+4=19(m).
答:这棵树原来的高度是19米.
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【6.1函数】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【6.1函数】(原卷版+解析),共27页。试卷主要包含了1 函数,03等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.2勾股定理的逆定理】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.2勾股定理的逆定理】(原卷版+解析),共21页。试卷主要包含了2 勾股定理的逆定理,3,0,5,2,2,5﹣4﹣2等内容,欢迎下载使用。
苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.1勾股定理】(原卷版+解析): 这是一份苏科版八年级数学上册同步考点必刷练精编讲义必刷提高练【3.1勾股定理】(原卷版+解析),共31页。试卷主要包含了1 勾股定理,8cm,,2cm,等内容,欢迎下载使用。













