2024河南中考数学复习 几何测量问题 强化精练 (含答案)

这是一份2024河南中考数学复习 几何测量问题 强化精练 (含答案)，共8页。


第1题图
A. 南偏西70°方向 B. 南偏东20°方向
C. 北偏西20°方向 D. 北偏东70°方向
2. (2023南充)如图，小兵同学从A处出发向正东方向走x米到达B处，再向正北方向走到C处，已知∠BAC＝α，则A，C处相距( )
A. eq \f(x,sin α) 米 B. eq \f(x,cs α) 米
C. x·sin α米 D. x·cs α米
第2题图
3. 如图，某地修建的一座建筑物的截面图的高BC＝5 m，坡面AB的坡度为1∶ eq \r(3) ，则AB的长度为( )
A. 10 m B. 10 eq \r(3) m
C. 5 m D. 5 eq \r(3) m
第3题图
4. (2023十堰)如图所示，有一天桥高AB为5米，BC是通向天桥的斜坡，∠ACB＝45°，市政部门启动“陡改缓”工程，决定将斜坡的底端C延伸到D处，使∠D＝30°，则CD的长度约为(参考数据： eq \r(2) ≈1.414， eq \r(3) ≈1.732)( )
A. 1.59米 B. 2.07米
C. 3.55米 D. 3.66米
第4题图
5. 如图，李老师用自制的直角三角形纸板去测“步云阁”的高度，他调整自己的位置，设法使斜边DF保持水平，边DE与点B在同一直线上．已知直角三角纸板中DE＝18 cm，EF＝12 cm，测得眼睛D离地面的高度为1.8 m，他与“步云阁”的水平距离CD为114 m，则“步云阁”的高度AB是( )
第5题图
A. 74.2 m B. 77.8 m
C. 79.6 m D. 79.8 m
6. [新考法——真实问题情境桔槔汲水](2023枣庄)如图所示，桔槔是一种原始的汲水工具，它是在一根竖立的架子上加上一根细长的杠杆，末端悬挂一重物，前端悬挂水桶．当人把水桶放入水中打满水以后，由于杠杆末端的重力作用，便能轻易把水提升至所需处，若已知：杠杆AB＝6米，AO∶OB＝2∶1，支架OM⊥EF，OM＝3米，AB可以绕着点O自由旋转，当点A旋转到如图所示位置时∠AOM＝45°，此时点B到水平地面EF的距离为______米．(结果保留根号)
第6题图
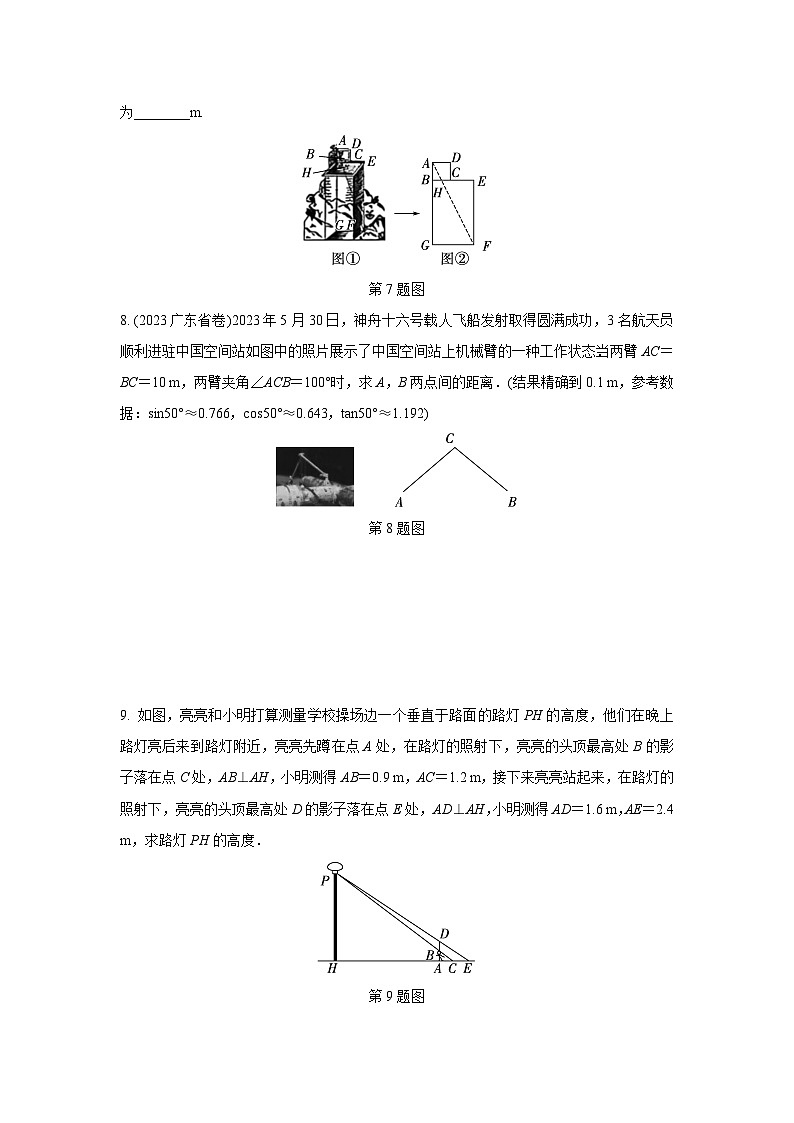
7. 四分仪是一种十分古老的测量仪器．其出现可追溯到数学家托勒密的《天文学大成》．图①是古代测量员用四分仪测量一方井的深度，将四分仪置于方井上的边沿，通过窥衡杆测望井底点F，窥衡杆与四分仪的一边BC交于点H.图②中，四分仪为正方形ABCD.方井为矩形BEFG.若测量员从四分仪中读得AB为1 m，BH为0.5 m，实地测得BE为2.5 m．则井深BG为________m.
第7题图
8. (2023广东省卷)2023年5月30日，神舟十六号载人飞船发射取得圆满成功，3名航天员顺利进驻中国空间站．如图中的照片展示了中国空间站上机械臂的一种工作状态．当两臂AC＝BC＝10 m，两臂夹角∠ACB＝100°时，求A，B两点间的距离．(结果精确到0.1 m，参考数据：sin50°≈0.766，cs50°≈0.643，tan50°≈1.192)
第8题图
9. 如图，亮亮和小明打算测量学校操场边一个垂直于路面的路灯PH的高度，他们在晚上路灯亮后来到路灯附近，亮亮先蹲在点A处，在路灯的照射下，亮亮的头顶最高处B的影子落在点C处，AB⊥AH，小明测得AB＝0.9 m，AC＝1.2 m，接下来亮亮站起来，在路灯的照射下，亮亮的头顶最高处D的影子落在点E处，AD⊥AH，小明测得AD＝1.6 m，AE＝2.4 m，求路灯PH的高度．
第9题图
拔高题
10. 如图，小明和小华利用学过的知识测量操场旗杆CD的高度，测量时，小明让小华站在点B处，此时，小华影子的顶端与旗杆的影子顶端在点E处重合，且BE的长为2米；小明又让小华沿着射线BD的方向走15.2米到达旗杆的另一侧N处，此时，小华观测到旗杆顶端C的仰角为45°，已知小华的身高为1.8米，请你根据相关测量信息，计算旗杆CD的高度．
第10题图
11. (2023甘肃省卷)如图①，某人的一器官后面A处长了一个新生物，现需检测其到皮肤的距离(图①).为避免伤害器官，可利用一种新型检测技术，检测射线可避开器官从侧面测量．某医疗小组制定方案，通过医疗仪器的测量获得相关数据，并利用数据计算出新生物到皮肤的距离．方案如下：
请你根据上表中的测量数据，计算新生物A处到皮肤的距离．(结果精确到0.1 cm)
(参考数据：sin35°≈0.57，cs35°≈0.82，tan35°≈0.70，sin22°≈0.37，cs22°≈0.93，tan22°≈0.40)
参考答案与解析
1. D 【解析】∵南北方向是平行的，∴淇淇家位于西柏坡的北偏东70°方向．
2. B 【解析】∵在Rt△ABC中，cs α＝ eq \f(AB,AC) ，∴AC＝ eq \f(AB,cs α) ＝ eq \f(x,cs α) .
3. A 【解析】∵坡面AB的坡度为 eq \f(BC,AC) ＝ eq \f(5,AC) ＝1∶ eq \r(3) ，∴AC＝5 eq \r(3) m，∴AB＝ eq \r(AC2＋BC2) ＝10 m.
4. D 【解析】在Rt△ABC中，∠BAC＝90°，∠ACB＝45°，∴∠ABC＝∠ACB＝45°，∴AC＝AB＝5米，在Rt△ABD中，∠BAD＝90°，∠D＝30°，∴ eq \f(AB,AD) ＝tan ∠ADB＝tan 30°＝ eq \f(\r(3),3) ，∴AD＝ eq \r(3) AB＝5 eq \r(3) ，∴CD＝AD－AC＝5 eq \r(3) －5≈1.732×5－5＝3.66(米)，∴CD的长度约为3.66米.
5. B 【解析】在△DEF和△DCB中，∵∠D＝∠D，∠DEF＝∠DCB＝90°，∴△DEF∽△DCB，∴ eq \f(DE,EF) ＝ eq \f(CD,CB) ，即 eq \f(18,12) ＝ eq \f(114,CB) ，解得CB＝76(m)，∵AC＝1.8 m，∴AB＝AC＋BC＝1.8＋76＝77.8(m)，即步云阁的高度AB是77.8 m.
6. 3＋ eq \r(2) 【解析】如解图，过点O作OC⊥BT，垂足为C，由题意得：BC∥OM，∴∠AOM＝∠OBC＝45°，∵AB＝6米，AO∶OB＝2∶1，∴AO＝4米，OB＝2米，在Rt△OBC中，BC＝OB·cs 45°＝2× eq \f(\r(2),2) ＝ eq \r(2) (米)，∵OM＝3米，∴此时点B到水平地面EF的距离＝BC＋OM＝(3＋ eq \r(2) )米．
第6题解图
7. 4 【解析】∵四边形ABCD是正方形，∴∠ABC＝90°，∵BE＝2.5 m，BH＝0.5 m，∴HE＝BE－BH＝2.5－0.5＝2 m，∵四边形BEFG是矩形，∴BG＝EF，∠BEF＝90°，∴∠HBA＝∠FEH＝90°，∵∠AHB＝∠FHE，∴△ABH∽△FEH，∴ eq \f(AB,FE) ＝ eq \f(BH,EH) ，∴ eq \f(1,EF) ＝ eq \f(0.5,2) ，∴EF＝4 m，∴BG＝EF＝4 m.
8. 解：如解图，连接AB，取AB中点D，连接CD，
∵AC＝BC，D为AB中点，
∴AD＝BD＝ eq \f(1,2) AB，∠ACD＝∠BCD＝ eq \f(1,2) ∠ACB＝50°，CD⊥AB，
在Rt△ACD中，sin ∠ACD＝ eq \f(AD,AC) ，
∴sin 50°＝ eq \f(AD,10) ，
∴AD＝10×sin 50°≈7.66(m)，
∴AB＝2AD＝2×7.66＝15.32≈15.3(m)，
答：A，B两点间的距离约是15.3 m．
第8题解图
9. 解：∵AB⊥AH，AD⊥AH，
∴△CBA∽△CPH，△EDA∽△EPH，
∴ eq \f(AB,HP) ＝ eq \f(AC,HC) ， eq \f(AD,HP) ＝ eq \f(AE,HE) ，
即 eq \f(0.9,HP) ＝ eq \f(1.2,HC) ， eq \f(1.6,HP) ＝ eq \f(2.4,HE) ，
∴CH＝ eq \f(4,3) PH，EH＝ eq \f(3,2) PH，
∴EH－CH＝ eq \f(1,6) PH＝CE＝AE－AC＝1.2，
∴PH＝7.2 m，
∴路灯PH的高度为7.2 m.
10. 解：如解图，连接AM交CD于点P，则AM⊥CD，PD＝AB＝MN＝1.8米，
设CP＝x米，
∵∠PMC＝45°，
∴PM＝CP＝x米，
∴AP＝(15.2－x)米，
∵AB∥CD，AM∥EN，
∴△ABE∽△CPA，
∴ eq \f(AB,CP) ＝ eq \f(BE,PA) ，
∴ eq \f(1.8,x) ＝ eq \f(2,15.2－x) ，
解得x＝7.2，
∴CP＝7.2米，
∴CD＝CP＋PD＝7.2＋1.8＝9(米).
答：旗杆CD的高度为9米．
第10题解图
11. 解：如解图，过点A作AF⊥MN，垂足为点F，
设BF＝x cm，
∵BC＝9 cm，
∴CF＝BC＋BF＝(x＋9)cm，
在Rt△ABF中，
∵∠ABF＝∠DBN＝35°，
∴AF＝BF·tan 35°≈0.7x(cm)，
在Rt△ACF中，
∵∠ACF＝∠ECN＝22°，
∴AF＝CF·tan 22°≈0.4(x＋9)cm，
∴0.7x＝0.4(x＋9)，
解得x＝12，
∴AF＝0.7x＝8.4(cm)，
答：新生物A处到皮肤的距离约为8.4 cm.
第11题解图
课题
检测新生物到皮肤的距离
工具
医疗仪器等
示意图
第11题图①
第11题图②
说明
如图②，新生物在A处，先在皮肤上选择最大限度地避开器官的B处照射新生物，检测射线与皮肤MN的夹角为∠DBN；再在皮肤上选择距离B处9 cm的C处照射新生物，检测射线与皮肤MN的夹角为∠ECN.
测量数据
∠DBN＝35°，∠ECN＝22°，BC＝9 cm