2024届中考数学制胜模拟卷及答案【云南专用】

这是一份2024届中考数学制胜模拟卷及答案【云南专用】，共16页。

一、选择题(本大题共15小题，每小题2分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的)
1．两千多年前，中国人就开始使用负数，如果支出150元记作元，那么元表示（ ）
A．收入100元B．支出100元C．收入50元D．支出50元
2．太湖龙之梦乐园自建成以来吸引了不少长三角地区游客前来游玩，该项目建造过程中总投资达251亿元，这个数据用科学记数法表示为（ ）
A．B．C．D．
3．如图是由5个完全相同的小正方体摆成的几何体，则这个几何体的主视图是（ ）
A．B．
C．D．
4．如果一个多边形的内角和是外角和的 5 倍，那么这个多边形的边数是（ ）
A．10B．11C．12D．13
5．观察图形并判断照此规律从左到右第四个图形是( )
A．B．C．D．
6．若关于的一元二次方程有两个实数根，则的取值范围是（ ）
A．B．C．且D．且
7．下列图形中既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
8．若点在反比例函数的图象上，则该图象也过点（ ）
A．B．C．D．
9．下列计算结果正确的是（ ）
A．B．C．D．
10．已知点在第二象限，则a的取值范围在数轴上表示是（ ）
A．B．
C．D．
11．一个直角三角形的一条直角边长为5，斜边长为13，则面积为（ ）
A．30B．32.5C．60D．75
12．估计的值应在（ ）
A．3和4之间B．4和5之间C．5和6之间D．6和7之间
13．大理古城简称榆城，位居风光亮丽的苍山脚下，是全国首批历史文化名城之一.它东临洱海，西枕苍山，城楼雄伟，风光优美，引来无数旅客前来观光.“十一”期间相关部门对到大理观光的游客的出行方式进行了随机抽样调查，整理绘制了两幅统计图（尚不完整），根据图中信息，下列结论错误的是（ ）

A．本次抽样调查的样本容量是5000
B．扇形统计图中的m为10%
C．样本中选择公共交通出行的约有2500人
D．若“十一”期间到大理观光的游客有50万人，则选择自驾方式出行的有25万人
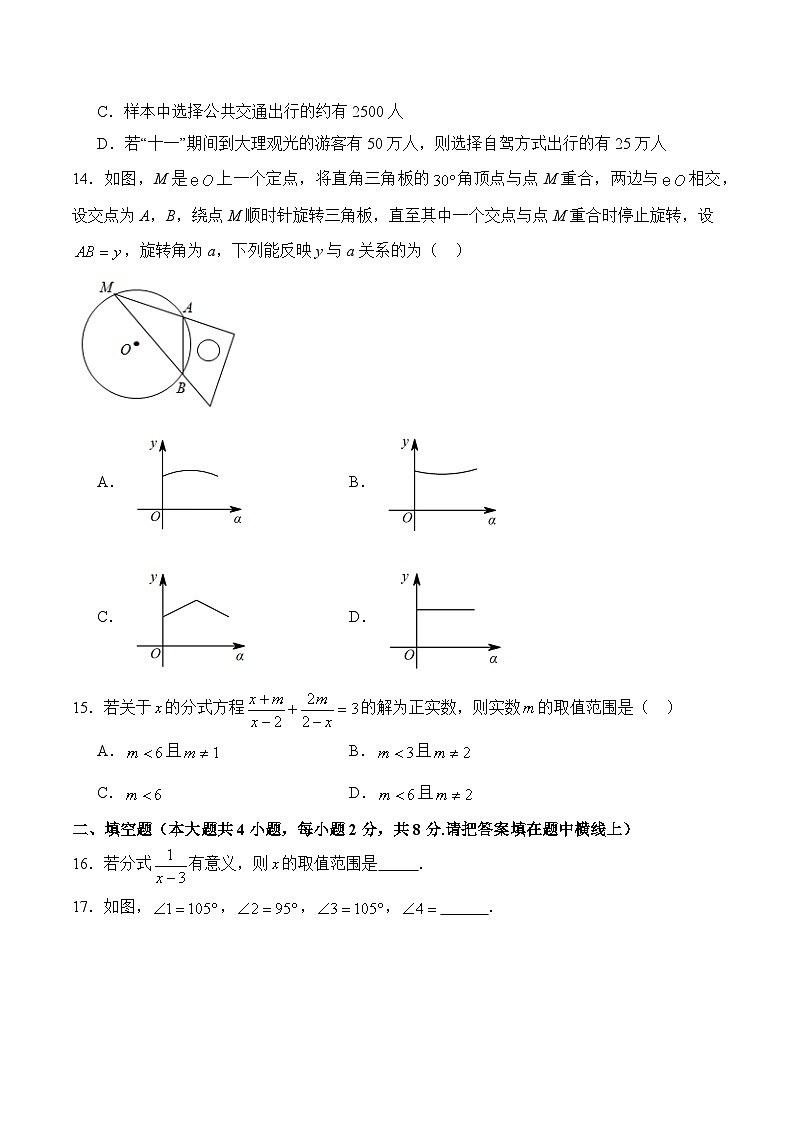
14．如图，M是上一个定点，将直角三角板的角顶点与点M重合，两边与相交，设交点为A，B，绕点M顺时针旋转三角板，直至其中一个交点与点M重合时停止旋转，设，旋转角为a，下列能反映y与a关系的为（ ）
A．B．
C．D．
15．若关于的分式方程的解为正实数，则实数的取值范围是（ ）
A．且B．且
C．D．且
二、填空题（本大题共4小题，每小题2分，共8分.请把答案填在题中横线上）
16．若分式有意义，则的取值范围是 ．
17．如图，，，， ．
18．已知数据a，b，c的平均数为8，那么数据，，的平均数是 ．
19．如图，菱形的对角线、相交于点，过点作于点，若，，则为 ．
三、解答题（本大题共8小题，共62分.解答应写出必要的文字说明，证明过程或演算步骤）
20．（7分）计算：．
21．（6分）某工厂为了完成供货合同，决定在一定天数内生产某种零件6000个，由于采用了新技术，每天比原计划增产20%，因此可提前20天完成任务，问原计划每天生产零件多少个？
22．（7分）如图，在四边形中，，．和是否全等？为什么？
23．（6分）经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，这三种可能性大小相同．
（1）一辆正常行驶的汽车经过某十字路口，则它向左转的概率为；
（2）现有甲、乙两辆汽车要经过这个十字路口，请用树形图或列表法表示出这两辆汽车行驶方向所有可能的结果，并求这两辆汽车都向左转的概率．
24．（8分）某宾馆有若干间标准房，经市场调查表明，每天入住的房间数y（间）与每间标准房的价格x（元）之间满足一次函数关系．当标准房的价格为200元时，每天入住的房间数为60间；当标准房的价格为210元时，每天入住的房间数为55间．该馆规定每间标准房的价格不低于170元，且不高于240元．
(1)求房间数y（间）与标准房的价格x（元）的函数关系式，并写出自变量x的取值范围．
(2)设客房的日营业额为w（元）．若不考虑其他因素，宾馆标准房的价格定为多少元时，客房的日营业额最大？最大为多少元？
25．（8分）如图，在中，，是的平分线，，交于点E，且．
(1)求证：是等腰三角形；
(2)求和的度数．
26．（8分）如图，在中，，平分交于点，为上一点，经过点，的分别交，于点，，连接．
(1)求证：是的切线；
(2)连接，求证：．
27．（12分）已知：抛物线．

(1)当时，求该抛物线的对称轴和顶点坐标；
(2)设该抛物线与轴交于，，与轴交于点，且满足，求这个抛物线的解析式；
(3)在（2）的条件下，是否存在着直线与抛物线交于点，使轴平分的面积？若存在，求出应满足的条件；若不存在，请说明理由．
答案以及解析
1．A
解：支出150元记作元，元表示收入100元，
故选：A．
2．C
解：251亿元=25100000000元=2.51×1010元，
故选C．
3．C
解：从正面看第一层是三个小正方形，第二层中间一个小正方形，
故选：C．
4．C
解；设这个多边形的边数是n，由题意得，，
解得，∴这个多边形的边数是12，
故选：C．
5．D
解：观察图形可知：单独涂黑的角顺时针旋转，只有D符合.
故选：D.
6．A
解：根据题意，，∴，
故选：．
7．C
解：A. ，是轴对称图形，不是中心对称图形，本选项不合题意；
B. ，不是轴对称图形，不是中心对称图形，本选项不合题意；
C. ，是轴对称图形，是中心对称图形，本选项符合题意；
D. ，不是轴对称图形，不是中心对称图形，本选项不合题意；
故选：C
8．A
解：∵点在反比例函数的图象上，∴，
A. ∵，则点在的图象上，故该选项正确，符合题意；
B. ∵，则点不在的图象上，故该选项不正确，不符合题意；
C. ∵，则点不在的图象上，故该选项不正确，不符合题意；
D. ∵，则点不在的图象上，故该选项不正确，不符合题意；
故选：A．
9．C
解：A、与无法合并，故选项错误，不符合题意；
B、，故选项错误，不符合题意；
C、，故选项正确，符合题意；
D、，故选项错误，不符合题意；
故选：C．
10．C
∵点在第二象限，
∴，
解第一个不等式得，解第二个不等式得
所以a<–1．
故选：C．
11．A
解：由题意可得，该直角三角形的另一直角边=，
∴该直角三角形的面积=.
故选A.
12．B
解：
即的值应在4和5之间；
故选：B．
13．D
解：A：本次抽样调查的样本容量是，选项A正确；
B：扇形统计图中，选项B正确；
C：样本中选择公共交通出行的人约有：（人），选项C正确；
D：50万游客中选择自驾方式出行的约有：（万人），选项D错误.
故选：D.
14．D
解：由题意可知，，∴线段的长度是不变的，
即随着旋转角a的变化，y的值是一个定值．
故选：D．
15．D
解：，
方程两边同乘得，，
解得，，
，，
由题意得，，解得，，
实数的取值范围是：且．
故选：D．
16．
解：∵分式有意义，∴，
∴，故答案为：．
17．85°
解：如图，∵∠1＝105°，∠3＝105°，
∴∠1＝∠3，
∴直线a∥直线b，
∴∠4＝∠5，
∵∠2＝95°，
∴∠4＝∠5＝180°−∠2＝85°，
故答案为：85°．
18．9
解：∵数据a，b，c的平均数为8，
∴，
∴，
∴，，的平均数．
故答案为9．
19．/4.8
解：四边形ABCD为菱形，，，
在中，
即
故答案为：．
20．0.
解：＝2﹣2﹣1+1＝0．
21．50
解：设原计划每天生产个零件
依题意得： ， 解得：
经检验是原方程的解，且符合题意
答：原计划每天生产50个零件。
22．；理由见解析．
解：；理由如下：
∵，，
∴，，
∴，
在与中，
∴．
23．；．
解：试题分析：根据题意画出表格，然后得出概率．
试题解析：（1）P（左转）=
（2）列表得：两辆汽车所有9种可能的行驶方向如下：
∴由上表知：P（两辆汽车都向左转的概率）=．
24．(1)，
(2)当宾馆标准房的价格定为170元时，客房的日营业额最大，最大为12750元
解：（1）解：设房间数y（间）与标准房的价格x（元）的函数关系式为，
由题意得，∴，
∴房间数y（间）与标准房的价格x（元）的函数关系式为；
（2）解：由题意得，
∵，∴当时，随x增大而减小，
∴当时，w最大，最大为，
∴当宾馆标准房的价格定为170元时，客房的日营业额最大，最大为12750元．
25．(1)见解析
(2)的度数为，的度数为
解：（1）证明：∵是的平分线，
∴ ，
∵，∴，
∵，∴，
∴，∴是等腰三角形；
（2）解：∵，
∴，
∵，∴，
∴，
∴的度数为，的度数为．
26．(1)见详解
(2)见详解
解：（1）证明：如图，连接，
，，
平分，，
，
，，
，，
是的切线．
（2）证明：如图，连接，
是直径，，
，，
，，
，
，，
，，
．
27．(1)对称轴直线，顶点坐标为
(2)
(3)存在，，且
解：（1）解：当时，得出，
求出对称轴直线，顶点坐标为．
（2）解：∵，∴，
又∵，∴，
∴.
∵ ，
∴，即，
∵ ，
∴，
化简得，解得（舍去）
∴解析式为．
（3）解：存在着直线与抛物线交于点，使轴平分的面积.
理由如下：
设点的横坐标为，点的横坐标为,直线与轴交于点.
∵ ，∴，
∴,
∵ 轴平分的面积，∴点在轴的异侧，即，
由得，为两根，
∴，∴
又∵直线与抛物线有两个交点，
∴.即.
∴当，且时，直线与抛物线交于点，使轴平分的面积．
乙汽车
甲汽车
左转
右转
直行
左转
（左转，左转）
（右转，左转）
（直行，左转）
右转
（左转，右转）
（右转，右转）
（直行，右转）
直行
（左转，直行）
（右转，直行）
（直行，直行）