江苏省苏州市昆山市2023-2024学年七年级下学期期末考试数学试题

这是一份江苏省苏州市昆山市2023-2024学年七年级下学期期末考试数学试题，共6页。试卷主要包含了06，人体内红细胞的直径大约为0，5×10⁻⁴ C，下列运算正确的是，计算等内容，欢迎下载使用。

2024.06
(满分130分,时间120分钟)
一、选择题：本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一项是符合题目要求的.请将选择题的答案用2B铅笔涂在答题卷相应位置上.
1.人体内红细胞的直径大约为0.00085cm，数据0.00085用科学记数法表示为
×10⁻³ B.8.5×10⁻⁴ C.85×10⁻⁵ D.8.5×10⁻⁴
2.下列运算正确的是
A.2a²+2a²=4a⁴ B.2a²-a²=2 C.3a²²=6a⁴ D.2a²⋅3a³=6a⁵
3.若a A.1-a>1-b B. a-1>b-1 C.a2>b2 D.a²>b²
4.下列命题中，是真命题的是
A.两条直线被第三条直线所截，内错角相等
B.若∠1 =∠2,则∠1与∠2 是对顶角
C.在同一平面内，垂直于同一直线的两条直线互相平行
D.如果 x²=y²,那么x=y
5.如图,在△ABC和△DEF中,点B,F,C,E在同一直线上,∠B=∠E,BF=EC,添加下列一个条件,仍不能判定△ABC≌△DEF的是
A. AB=DE B. AC=DF C.∠A=∠D D.∠ACB=∠DFE
6.我国古典数学文献《增删算法统宗·六均输》中这样一个题：“甲乙隔沟牧放，二人暗里参详，甲云得乙九只羊，多乙一倍之上，乙说得甲九只，两家之数相当”.译文：甲、乙两人一起放牧，两人心里暗中数羊.如果乙给甲9只羊，那么甲的羊数为乙的2倍；如果甲给乙9只羊，那么两人的羊数相同，请问原来甲，乙各有多少只羊?设原来甲有羊x只，乙有羊y只，则符合题意的方程组是
A.x+9=2yx-9=y+9 B.x+9=2y-9x-9=y+9 C.x-9=2y+9x+9=y-9 D.x+9=2y-9x-9=y+9
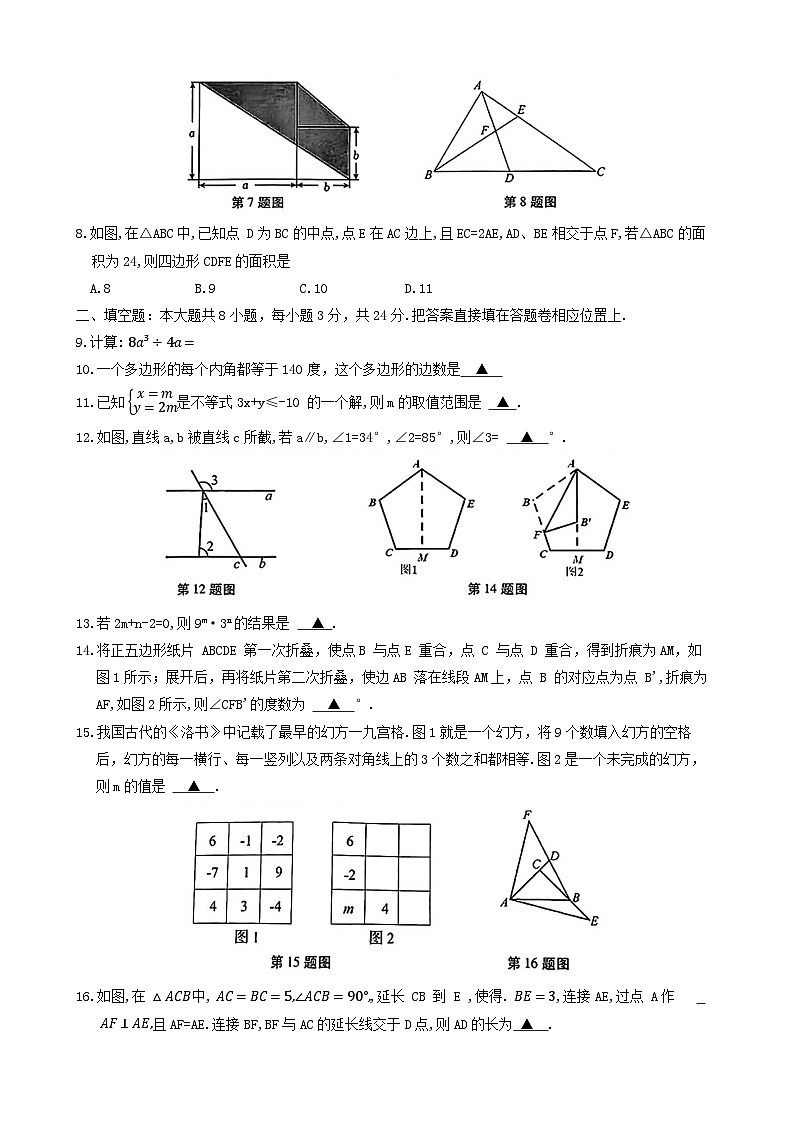
7.边长分别为a和b(其中a>b)的两个正方形按如图摆放，如果a+b=6，ab=8，则图中阴影部分的面积为
A.8.5 B.10 C.18 D.36
8.如图,在△ABC中,已知点 D为BC的中点,点E在AC边上,且EC=2AE,AD、BE相交于点F,若△ABC的面积为24,则四边形CDFE的面积是
A.8 B.9 C.10 D.11
二、填空题：本大题共8小题，每小题3分，共24分.把答案直接填在答题卷相应位置上.
9.计算: 8a³÷4a=
10.一个多边形的每个内角都等于140度，这个多边形的边数是 ▲
11.已知 x=my=2m是不等式3x+y≤-10 的一个解,则m的取值范围是 ▲ .
12.如图,直线a,b被直线c所截,若a∥b,∠1=34°,∠2=85°,则∠3= ▲ °.
13.若2m+n-2=0,则9m·3n的结果是 ▲ .
14.将正五边形纸片 ABCDE 第一次折叠，使点B 与点E 重合，点 C 与点 D 重合，得到折痕为AM，如图1所示；展开后，再将纸片第二次折叠，使边AB 落在线段AM上，点 B 的对应点为点 B',折痕为AF,如图2所示,则∠CFB'的度数为 ▲ °.
15.我国古代的《洛书》中记载了最早的幻方一九宫格.图1就是一个幻方，将9个数填入幻方的空格后，幻方的每一横行、每一竖列以及两条对角线上的3个数之和都相等.图2是一个未完成的幻方，则m的值是 ▲ .
16.如图,在 △ACB中, AC=BC=5,∠ACB=90°,,延长 CB 到 E ,使得. BE=3,连接AE,过点 A作 AF⊥AE,且AF=AE.连接BF,BF与AC的延长线交于D点,则AD的长为 ▲ .
三、解答题：本大题共11小题，共82分.把解答过程写在答题卷相应位置上，解答时应写出必要的计算过程、推演步骤或文字说明.作图时用2B铅笔或黑色墨水签字笔.
17.(本题满分4分)计算: |-1|-π+2024⁰+2⁻².
18.(本题满分8分)因式分解： 1a³-9a; 2-x²+4xy-4y².
19.(本题满分9分)(1)解方程组: 2x-2y+1=4,3x+y=5 (2)解不等式组： 6x-2≤4x,2x+45-x2<1
20.(本题满分6分)化简求值： 2x+1²-x+2x-2+2xx-1,其中 3x²+2x-1=0.
21.(本题满分6分)如图,在△ABC中,AD⊥BC于点 D.
(1)作 ∠ABC的角平分线，交AD 于点E，交AC于点F；(要求：尺规作图，保留作图痕迹，不必写作法)
(2)在(1)的条件下,若∠ ∠BAC=80°,∠C=62°,求∠AEF 的度数.
22.(本题满分6分)观察下列算式，解答下列问题：
第1 个算式： 3²-1²=8×1,
第2个算式： 5²-3²=8×2,
第3个算式： 7²-5²=8×3,
………
第n个算式: .
(1)根据上述算式的规律，直接写出第4个算式 ▲ ；
(2)用字母n(n为正整数)表示数，写出第n个算式，并证明这个算式的正确性.
23.(本题满分7分)如图,在△ABC中,D为AC中点,F为AB边上一点,连接FD,并延长FD至点 E,使得 ED=DF,连接CE.
(1)求证:△CDE≌△ADF ;
(2)若EF∥BC,∠A=60°,∠E=50°,求∠BCD的度数.
24.(本题满分8分)根据下表信息，探索完成任务.

25.(本题满分8分)数学综合实践课上，小明用一块直角三角板 COD 进行探究：将三角板的直角顶点 O 放在直线AB 上，将边 OC 落在射线 OA 上，边 OD 位于直线 AB 上方，三角板COD 绕点 O 顺时针旋转，旋转角为a，作直线OE平分. ∠BOC交CD所在直线于点 E.
(1)提出问题:如图1,若旋转角a=70°,求∠DOE的度数;
(2)探索发现：如图2，若旋转角 a(90°(3)拓展探究：继续旋转三角板，若旋转角 a(180°26.(本题满分10分)对x、y定义一种新运算T，规定： Txy=ax+by+4(其中a、b均为非零常数).例如： T00=a×0+b×0+4=4,已知 T11=5,T-12=0.
(1) 则 a=,b=;
(2)已知 m>0,n≥0,且 Tm-n=6,,求 T(3m,n)的取值范围;
(3)求 T2x²4y+T2y²-4x的最小值.
27.(本题满分10分)如图,在 △ABC和 △ADE中，已知 ∠BAC=∠DAE=90°,AB=AC,AD=AE.
(1)如图1,求证: CD=BE;
(2)当C、B、E三点在一条直线上时，
①如图2，已知 ∠BDC=60°,求 ∠DBE的度数；
②如图3,过A作 AF⊥BD交AD于点 F,若 AF=4,△AEC的面积为13,求 BD的长.
背景
某校组织七年级师生到全国中小学生研学实践教育基地沙家浜开展春季研学活动，需要联系客运公司租用客车乘车前往.
信息1
租用3辆甲型客车和1辆乙型客车满载能坐师生170人；租用1辆甲型客车和2辆乙型客车满载能坐师生140人.
信息2
本次参加研学的师生共有505人；甲型客车每辆租金800元，乙型客车每辆租金900元.
信息3
学校计划租甲、乙两种型号客车共11辆，在保证一次性将全部师生送到目的地的前提下，租车费用不超过9600元.
任务解决
任务1
每辆甲型客车和乙型客车各能坐多少人?
任务2
有哪几种租车方案?