福建省福州市仓山区2021-2022学年五年级下学期期中数学试卷

这是一份福建省福州市仓山区2021-2022学年五年级下学期期中数学试卷，共15页。试卷主要包含了冷静思考，正确填空，反复比较，慎重选择，观察分析，实践操作，活用知识，解决问题等内容，欢迎下载使用。

1．在括号里填上适当的单位名称。
一个小轿车油箱的容积是30 （ ）
喜多每步长度约是60（ ）
一间教室大约占地48（ ）
2．3个是 ，里有 个，1里面有 个。
3．在1、2、9、13、14这些数中，既是偶数又是质数的是 ，既是奇数又是合数的是 。
4．6.3L＝ mL
540cm2＝ dm2
5．根据12÷m＝n（m和n均为非0自然数），那么12是 和 的倍数， 和 是 的因数。
6．分数单位是的最大真分数是 ，最小假分数是 。
7．a是一个奇数，与它相邻的两个偶数是 和 ．
8．用18个边长是1cm的小正方形摆成一个长方形，有 种摆法。
9．如图所示图形至少还需要 个这样的小正方体才能拼成一个大正方体。
10．7□3□同时是2和3的倍数，这个四位数最小是 ，最大是 。
11．一个长方体，相交于一个顶点的三条棱的长度分别是6dm、4dm、3dm。如果把这个长方体放在地面上，最大占地面积是 dm2，它的体积是 dm3。
12．如图阴影部分的面积占整个图形面积的 。
二、反复比较，慎重选择（把正确答案的序号填在括号里）。
13．一个可乐瓶上标着1.25L，说明瓶中可乐的（ ）是1.25L。
A．表面积B．重量C．体积D．容积
14．下列图形中，涂色部分正好占整个图形的的是（ ）
A．B．C．D．
15．下面各数中，（ ）既是2、5的倍数，又是3的倍数。
A．135B．130C．123D．120
16．下列的算式，结果是奇数的是（ ）
A．128﹣54B．21×57C．17+123D．94×5
17．有2袋橙子，每袋6千克，平均分给3个小朋友，每个小朋友分得（ ）袋。
A．2B．C．D．
18．一个正方体的棱长是一个质数，它的体积一定是（ ）
A．合数B．质数C．奇数D．偶数
19．把7g糖溶入100g水中，水的质量占糖水的（ ）
A．B．C．D．
20．如图这个组合体，从（ ）看到的形状相同。
A．正面和上面B．左面和上面
C．正面和左面D．正面、左面和上面
21．如图两个图形分别表示一个长方体的底面和右面，那么这个长方体前面的面积是（ ）平方厘米。（单位：cm）
A．15B．24C．40D．120
22．如图是小明求鹅卵石体积的实验过程，下列算式中（ ）能正确求出鹅卵石的体积．（单位：cm）
A．12×8×8B．12×8×9
C．12×8×（12﹣9）D．12×8×（9﹣8）
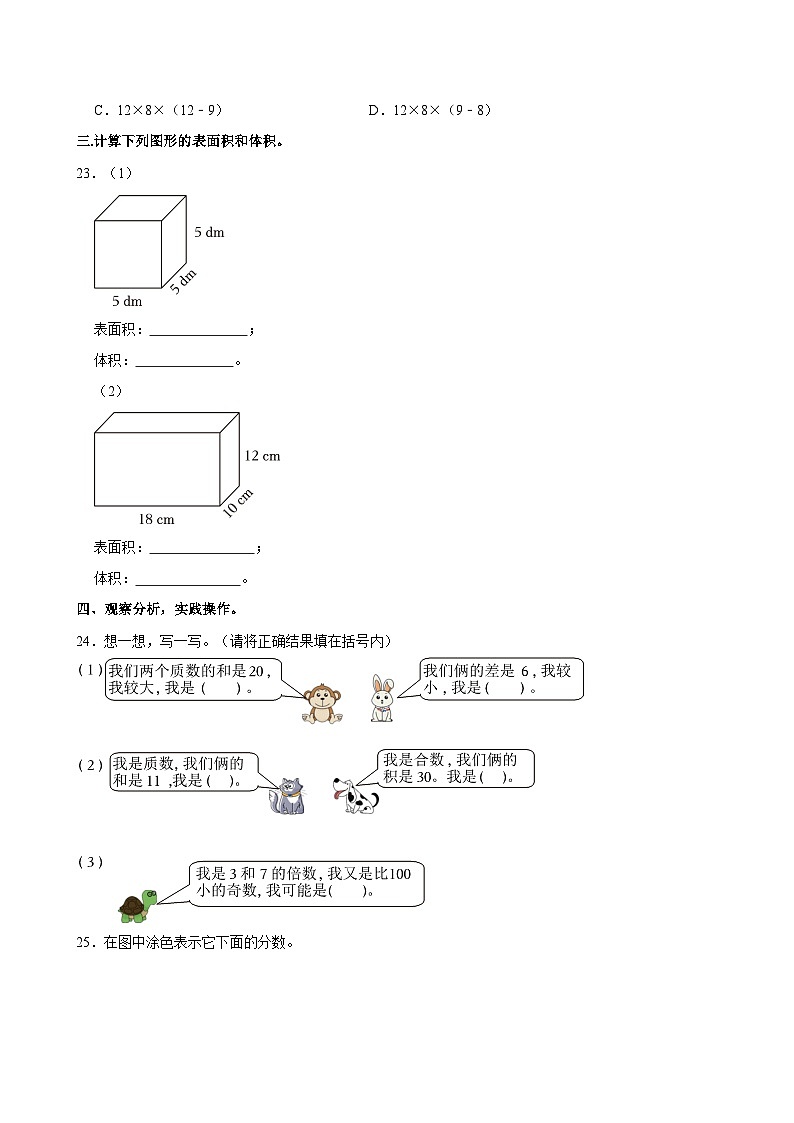
三.计算下列图形的表面积和体积。
23．（1）
表面积： ；
体积： 。
（2）
表面积： ；
体积： 。
四、观察分析，实践操作。
24．想一想，写一写。（请将正确结果填在括号内）
25．在图中涂色表示它下面的分数。
26．用同样大小的正方体搭出了下面的几个几何体。
（1）从正面看是的有 。
（2）从左面看是的有 。
（3）从上面看是的有 。
27．请在方格中画出如图所示几何体从三个方向看到的形状。
五、活用知识，解决问题。
28．把一袋4千克的葡萄平均分给5个小朋友，每人分得这袋葡萄的几分之几？每人分得多少千克？
29．要制作一个外卖箱，需先用玻璃钢这种材料构造出长方体支架，然后套上一层内层含有铝箔的牛津防水布。
（1）要制作如图所示的外卖箱至少需多少玻璃钢？（忽略牛津防水布厚度）
（2）制作这款外卖箱至少需多少牛津防水布？
（3）此款外卖箱从里面量长43cm、宽30cm、高31cm，它的容积是多少升？
（4）若要送长21.4cm、宽15cm、高5cm的外卖盒饭，一次最多可以送多少盒？
一块棱长为5cm的正方体铁块放在一个长12cm，宽10cm，高8cm的玻璃缸中，至少向玻璃缸中加多 少毫升的水才能没过正方体？
2021-2022学年福建省福州市仓山区五年级（下）期中数学试卷
参考答案与试题解析
一、冷静思考，正确填空。
1．【分析】根据生活经验、对面积单位、体积单位和数据大小的认识，可知计量一个小轿车油箱的容积应用“升”作单位；计量喜多每步长度应用“厘米”作单位；计量一个教室的占地面积应用“平方米”作单位；据此进行填空即可。
【解答】解：一个小轿车油箱的容积是30升；
喜多每步长度约是60厘米；
一间教室大约占地48平方米。
故答案为：升，厘米，平方米。
2．【分析】把单位“1”平均分成若干份取一份的数，叫做分数单位；分数的分子是几里面就有几个这样的分数单位。
【解答】解：3个是 ，里有4个，1里面有10个。
故答案为：， 4，10。
3．【分析】偶数：是2的倍数的数叫做偶数，又叫做双数，如：2、4、6、8等，奇数：不是2的倍数的数叫做奇数，又叫做单数，合数：指自然数中除了能被1和本身整除外，还能被其他的数整除的数，“0”“1”既不是质数也不是合数，质数：一个数只有1和它本身两个因数，这个数叫作质数。
【解答】解：在1、2、9、13、14这些数中，既是偶数又是质数的是2，既是奇数又是合数的是9。
故答案为：2；9。
4．【分析】1升＝1000毫升，1平方分米＝100平方厘米，单位之间的换算，大单位换算成小单位要乘它们之间的进率；小单位换算成大单位要除以它们之间的进率。
【解答】解：6.3L＝6300mL
540cm2＝5.4dm2
故答案为：6300，5.4。
5．【分析】若整数a能够被b整除，a叫做b的倍数，b就叫做a的因数，因数与倍数是相互依存的，据此解答。
【解答】解：根据12÷m＝n（m和n均为非0自然数），那么12是m和n的倍数，m和n是 12的因数。
故答案为：m，n；m，n，12。
6．【分析】分母是99，分子比分母小的最简分数是真分数，分子大于或等于分母的分数是假分数。
【解答】解：分数单位是的最大真分数是，最小假分数是。
故答案为：；。
7．【分析】不是2的倍数的自然数，叫做奇数；是2的倍数的自然数，叫做偶数；据此可知，相邻的三个自然数，要么有两个是奇数，一个是偶数，要么有两个是偶数，一个是奇数；据此解答．
【解答】解：如果a是一个奇数，那么与a相邻的两个偶数分别是：a﹣1和a+1．
故答案为：a﹣1和a+1．
8．【分析】因为18＝6×3＝9×2＝18×1，所以用18个边长为1厘米的小正方形可以摆成长6厘米、宽3厘米的长方形，也可以摆成长9厘米、宽2厘米的长方形，还可以摆成长18厘米、宽1厘米的长方形，共有3种不同的摆法。
【解答】解：根据分析可知；用18个边长1厘米的小正方形拼成一个大的长方形的方法共3种，如图：
答：有3种不同的摆法。
故答案为：3。
9．【分析】观察图形可知：拼组后的大正方体的每条棱长至少是由2个小正方体组成的，由此可以求出拼组后的大正方体中的小正方体的个数，再减去图中已有的小正方体个数即可。
【解答】解：2×2×2＝8（个）
8﹣4＝4（个）
答：至少还需要4个这样的小正方体，才能搭拼成一个大正方体。
故答案为：4。
10．【分析】同时是2和3的倍数的数的特征：个位上是0、2、4、6、8且各个数位上的数加起来能被3整除。
【解答】解：7+3＝10
10+2＝12
12能被3整除。
9+8＝17
10+17＝27
27能被3整除。
答：这个四位数最小是7032，最大是7938。
故答案为：7032；7938。
11．【分析】最大占地面积等于长是6分米，宽是4分米的长方形的面积，利用长方体的体积＝长×宽×高计算长方体的体积。
【解答】解：6×4＝24（平方分米）
6×4×3＝72（立方分米）
答：最大占地面积是24平方分米，体积是72立方分米。
故答案为：24；72。
12．【分析】利用拼移法把阴影移到下面的带有阴影的正方形内，数一下阴影正方形的数量，再数一下所有正方形的数量即可，利用分数的意义解答。
【解答】解：1÷4＝
答：阴影部分的面积占整个图形面积的。
故答案为：。
二、反复比较，慎重选择（把正确答案的序号填在括号里）。
13．【分析】体积和容积是两个不同的概念，意义不同：容积是指容器所能容纳物体的体积，箱子、油桶、仓库等所能容纳物体的体积，叫做它们的容积或容量；物体所占的空间的大小叫做体积。
【解答】解：一个可乐瓶上标着1.25L，说明瓶中可乐的容积是1.25L。
故选：D。
14．【分析】A、把一个正方形的面积分成4份，其中1份涂色，由于不是平均分成，因此，涂色的1份不占整个图形的；
B、把一个圆的面积看作单位“1”，把它平均分成4份，每份是它的，其中1份涂色，占整个图形的；
C、把一个圆的面积分成4份，其中1份涂色，由于不是平均分成，因此，涂色的1份不占整个图形的；
D、把一个三角形的面积分成4份，其中1份涂色，由于不是平均分成，因此，涂色的1份不占整个图形的。
【解答】解：涂色部分正好占整个图形的的是：
故选：B。
15．【分析】既是2、5的倍数，又是3的倍数的数的特征：个位上是0，各个数位上的数加起来能被3整除。
【解答】解：A.135个位上不是0，故不符合题意；
B.130个位上是0，1+3＝4，4不能被3整除，故不符合题意；
C.123个位上不是0，故不符合题意；
D.120个位上是0，1+2＝3，3能被3整除，故符合题意。
故选：D。
16．【分析】偶数：是2的倍数的数叫做偶数，又叫做双数，如：2、4、6、8等，奇数：不是2的倍数的数叫做奇数，又叫做单数。
【解答】解：A.128﹣54＝74，74是偶数
B.21×57＝1197，1197是奇数；
C.17+123＝140，140是偶数；
D.94×5＝470；470是偶数。
故选：B。
17．【分析】把2袋橙子的质量看作单位“1”，把它平均分成3份，求每份的质量，用橙子的质量除以小朋友人数。
【解答】解：2÷3＝（千克）
答：每个小朋友分得袋。
故选：D。
18．【分析】由于正方体体积公式：V＝a3，可知a3的因数有1，a3，a，a2，再根据合数与质数的定义即可求解。
【解答】解：因为正方体体积公式：V＝a3，立方体的棱长是一个质数，
a3的因数除了1，a3，还有a，a2，
所以它的体积一定是合数。
故选：A。
19．【分析】用糖的质量加上水的质量，求出糖水的质量，用水的质量除以糖水的质量，即可解答。
【解答】解：100÷（7+100）
＝100÷107
＝
答：水的质量占糖水的。
故选：D。
20．【分析】如图这个组合体，从正面和上面看到的形状是；从左面看到的形状是；据此解答即可。
【解答】解：如图这个组合体，从正面和上面看到的形状相同。
故选：A。
21．【分析】根据长方体的特征可知，长方体底面是一个长8厘米宽3厘米的长方形，右面的一个长5厘米，宽3厘米的长方形，也就是这个长方体的长是8厘米，宽是3厘米，高是5厘米，根据长方形的面积公式：S＝ab，把数据代入公式解答。
【解答】解：8×5＝40（平方厘米）
答：这个长方体前面的面积是40平方厘米。
故选：C。
22．【分析】这块石头的体积等于上升的（9﹣8＝1）厘米水的体积，用底面积（长×宽）乘上升的厘米数即可．
【解答】解：12×8×（9﹣8）
＝96×1
＝96（立方厘米）
答：鹅卵石的体积是96立方厘米．
故选：D．
三.计算下列图形的表面积和体积。
23．【分析】（1）根据正方体的表面积公式：S＝6a2，体积公式：V＝a3，把数据代入公式解答。
（2）根据长方体的表面积公式：S＝（ab+ah+bh）×2，体积公式：V＝abh，把数据代入公式解答。
【解答】解：（1）5×5×6
＝25×6
＝150（平方分米）
5×5×5
＝25×5
＝125（立方分米）
答：它的表面积是150平方分米，体积是125立方分米。
（2）（18×10+18×12+10×12）×2
＝（180+216+120）×2
＝516×2
＝1032（平方厘米）
18×10×12
＝180×12
＝2160（立方厘米）
答：它的表面积是1032平方厘米，体积是2160立方厘米。
故答案为：150平方分米，125立方分米；1032平方厘米，2160立方厘米。
四、观察分析，实践操作。
24．【分析】（1）两个质数的和是20，则这两个质数是3和17，7和13；两个质数的差是6，所以这两个质数是7和13；
（2）一个质数和一个合数的和是11，则这两个数是2和9，3和8，5和6；这两个数乘积是30，所以这两个数是5和6；
（3）3和7的倍数有21，42，63，84；又比100小的奇数，这个数是21或63。
【解答】解：由分析可知：
故答案为：13，7；5，6；21。（答案不唯一）
25．【分析】用涂色部分表示分数时，把总体平均分成的份数作分数的分母，涂色部分所占的份数作分数的分子。
【解答】解：
26．【分析】①号立体图形：从正面能看到5个相同的正方形，分两层，上层2个，下层3个，左齐；从左面能看到一列2个相同的正方形；从上面能看到一行3个相同的正方形。
②号立体图形：从正面能看到4个相同的正方形，分两层，上层1个，下层3个，右齐；从左面能看到3个相同的正方形，分两层，上层1个，下层2个，左齐；从上面能看到4个相同的正方形，分两层，上层3个，下层1个，左齐。
③号立体图形：从正面能看到4个相同的正方形，分两层，下层3个，上层居中1个；从左面能看到3个相同的正方形，分两层，上层1个，下层2个，左齐；从上面能看到4个相同的正方形，分两层，上层3个，下层居中1个。
④号立体图形：从正面能看到4个相同的正方形，分两层，下层3个，上层居中1个；从左面能看到一列2个相同的正方形；从上面能看到一行3个相同的正方形。
⑤号立体图形：从正面能看到5个相同的正方形，分两层，上层2个，下层3个，两端齐；从左面能看到一列2个相同的正方形；从上面能看到一行3个相同的正方形。
⑥号立体图形：从正面能看到5个相同的正方形，分两层，上层2个，下层3个，两端齐；从左面能看到3个相同的正方形，分两层，上层1个，下层2个，左齐；从上面能看到4个相同的正方形，分两层，每层2个，上层左与下层右齐。
【解答】解：如图：
（1）从正面看是的有③、④、⑥。
（2）从左面看是的有②、③、⑥。
（3）从上面看是的有①、④、⑤。
故答案为：③、④、⑥；②、③、⑥；①、④、⑤。
27．【分析】根据观察物体的方法，几何体从正面看到2层，底层3个小正方形，上层1个小正方形居中；从左面看到2层，底层3个小正方形，上层2个小正方形，左齐；从上面看到三层，底层2个小正方形和中间层3个小正方形右齐，上层1个小正方形居中，据此解答即可。
【解答】解：如图：
五、活用知识，解决问题。
28．【分析】把一袋4千克的葡萄看作单位“1”，平均分给5个小朋友，每人分得这袋葡萄的1÷5＝，每人分得多少千克，用总千克数除以人数。
【解答】解：1÷5＝
4÷5＝（千克）
答：每人分得这袋葡萄的，每人分得千克。
29．【分析】（1）根据长方体的棱长总和＝（长+宽+高）×4，把数据代入公式解答。
（2）根据长方体的表面积公式：S＝（ab+ah+bh）×2，把数据代入公式解答。
（3）根据长方体的体积（容积）公式：V＝abh，把数据代入公式解答。
（4）首先根据“包含”除法的意义，用除法分别求出这个外卖箱的长、宽、高里面各包含多少个外卖盒的长、宽、高，然后用乘法解答。
【解答】解：（1）（45+32+35）×4
＝112×4
＝448（厘米）
答：至少需要448厘米的玻璃钢。
（2）（45×32+45×35+32×35）×2
＝（1440+1575+1120）×2
＝4135×2
＝8270（平方厘米）
答：至少需要8270平方厘米的牛津防水布。
（3）43×30×31
＝1290×31
＝39990（立方厘米）
39990立方厘米＝39.99（升）
答：它的容积是39.99升。
（4）43÷21.4≈2（个）
30÷15＝2（个）
31÷5≈6（个）
2×2×6＝24（盒）
答：一次最多可以送24盒。
30．【分析】根据题意可知，当加入水的高度等于正方体的棱长时，水才会没过正方体，用长方体的底面积减去正方体的底面积，然后乘5即可。
【解答】解：（12×10﹣5×5）×5
＝（120﹣25）×5
＝95×5
＝475（立方厘米）
475立方厘米＝475毫升
答：至少向玻璃缸中加475毫升的水才能没过正方体。