海南省海口市丰南中学2023-2024学年八年级下学期期中数学试题

这是一份海南省海口市丰南中学2023-2024学年八年级下学期期中数学试题，共8页。试卷主要包含了答题前请认真阅读试题有关说明，请合理分配答题时间，如图，已知平行四边形中，，则，已知函数，自变量的取值范围是，关于的分式方程有增根，则的值等内容，欢迎下载使用。

时间：100分钟 满分：120分
特别提醒：
1.答案一律用黑色笔填写在答题卡上，写在试题上无效。
2.答题前请认真阅读试题有关说明。
3.请合理分配答题时间。
一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.）
1.下列各式中不属于分式的是（ ）
A.B.C.D.
2.计算的结果是（ ）
A.B.C.D.
3.下列各点在函数图象上的是（ ）
A.B.C.D.
4.我国古代数学家祖冲之推算出的近似值为，它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为（ ）
A.B.C.D.
5.如图，已知平行四边形中，，则（ ）
A.B.C.D.
6.已知函数，自变量的取值范围是（ ）
A.B.且C.D.
7.若点在第二象限内，点到轴的距离是3，到轴的距离是5，则点的坐标（ ）
A.B.C.D.
8.关于的分式方程有增根，则的值（ ）
A.B.C.D.
9.一次函数与反比例函数在同一坐标系中的大致图象是（ ）
A.B.C.D.
10.若点，，都在反比例函数的图像上，则，，的大小关系是（ ）
A.B.C.D.
11.如图，在中，，，平分线交于点，交的延长线于点，则的长是（ ）
A.2B.3C.4D.5
12.如图，中，，，为边上的一动点，以，为边作平行四边形，则线段长度的最小值为（ ）
A.6B.8C.D.
第II卷（非选择题）
二、填空题（本题共4小题，每小题3分，共12分）
13.比较大小：______.（选填>，=，<）
14.将直线沿轴向上平移2个单位，得直线的函数解析式为______.
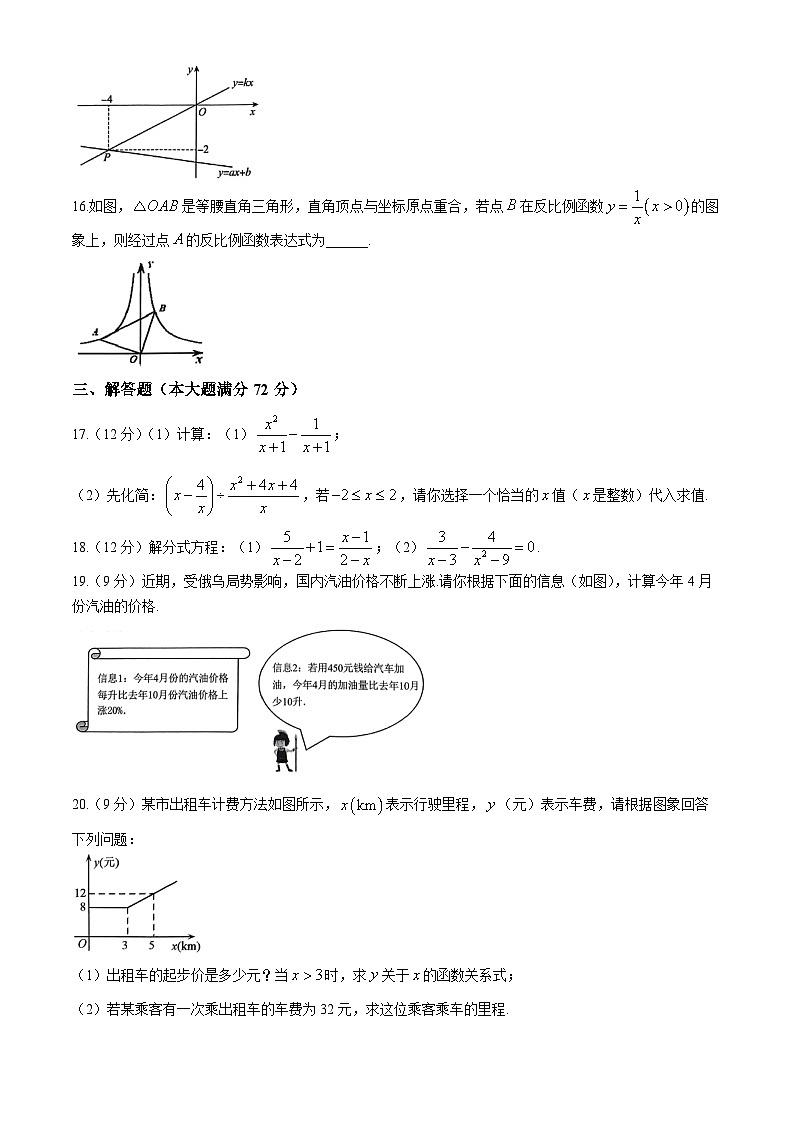
15.如图，已知函数和的图象交于点，关于，的方程组的解是______.
16.如图，是等腰直角三角形，直角顶点与坐标原点重合，若点在反比例函数的图象上，则经过点的反比例函数表达式为______.
三、解答题（本大题满分72分）
17.（12分）（1）计算：（1）；
（2）先化简：，若，请你选择一个恰当的值（是整数）代入求值.
18.（12分）解分式方程：（1）；（2）.
19.（9分）近期，受俄乌局势影响，国内汽油价格不断上涨.请你根据下面的信息（如图），计算今年4月份汽油的价格.
20.（9分）某市出租车计费方法如图所示，表示行驶里程，（元）表示车费，请根据图象回答下列问题：
（1）出租车的起步价是多少元？当时，求关于的函数关系式；
（2）若某乘客有一次乘出租车的车费为32元，求这位乘客乘车的里程.
21.（15分）【教材呈现】如图是华师版八年级下册数学教材第77页的部分内容.
请根据教材提示，结合上图，写出完整的证明过程.
【性质应用】如图，在中，对角线，相交于点，过点且与边，分别相交于点，.
求证：.
【拓展提升】在【性质应用】的条件下，连结.若，的周长是13，则的周长是______.
22.（15分）如图，一次函数的图象与反比例函数的图象交于，两点，连结，.
（1）求一次函数和反比例函数的表达式；
（2）求的面积；
（3）根据函数图象，写出不等式的解集：______
（4）点是轴上的一个动点，连结、；当是等腰三角形时，直接写出点坐标.
2023-2024学年度第二学期
八年级数学科期中检测试题答案
一、选择题（每小题3分，共36分）
BCDABBBDBBBD
二、填空题（每小题3分，共12分）
13.14.15.16.
三、解答题（共72分）
17.每小题6分，共12分
（1）解：
；
（2）解：
满足，若取整数，使所求式子有意义，则可取、1、2，取一个值计算即可；
当时，原式
当时，原式
当时，原式
18.（1）解：，
去分母得：，
移项合并同类项得：，
系数化为1得：，
检验：把代入得：，
是原方程的解；
（2）解：，
去分母得：，
去括号得：，
移项合并同类项得：，
系数化为1得：，
检验：把代入得：，
是原方程的解.
19.解：设去年10月份汽油的价格为每升元，
由题意得，
解得：，
经检验是原方程的解，
，
今年4月份汽油的价格为每升9元，
答：今年4月份汽油的价格为每升9元.
20.（1）由图象可知，出租车的起步价为8元.
当时，设函数表达式为.
图象经过，，
解得
当时，关于表达式为.
（2）当时，由，解得，
这位乘客乘车的里程是15千米.
21.[教材呈现]证明：四边形是平行四边形，
，，
，，
在和中，
，
，；
[性质应用]证明：四边形是平行四边形，
，，
，，
在和中，
；
[拓展提升]解：如图，，
，
，
是等腰三角形，
，
，
的周长，
四边形是平行四边形，
，，
的周长，
答案：26.
22.答案：（1）一次函数的表达式为；反比例函数的表达式为
（2）
（3）或
解析：（1）把点代入，得，
解得，
一次函数的表达式为，
把点代入得，
反比例函数的表达式为.
（2）设直线与轴的交点为，
在中，令，则，
点的坐标为，
，把点代入，得，
点的坐标为.
.
（3）由（2）得：，
点的坐标为，
不等式的解集为：或，
故答案为：或.
（4）；；；；.
（注：此题结果中，不化简不扣分.用其它方法求解参照以上标准给分.）
平行四边形的性质定理3平行四边形的对角线互相平分.
我们可以用演绎推理证明这个结论.
已知：如图，的对角线和相交于点.
求证：，.