数学：山东省临沂市郯城县2024年九年级中考二模试题 （解析版）

这是一份数学：山东省临沂市郯城县2024年九年级中考二模试题 （解析版），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 下列四个数中，绝对值最大的是（ ）
A. 0B. C. D.
【答案】C
【解析】∵，
∴，
∴绝对值最大的是．
故选：C．
2. 山东临沂，历史悠久，文化灿烂，是沂蒙精神的发源地．这里风景秀美，人文荟萃，多个地标性建筑不仅展现了地方特色，更展现了中国文化的对称之美，让人流连忘返．下列图形中，不是轴对称图形的是（ ）
A. B.
C. D.
【答案】A
【解析】A、不是轴对称图形，故本选项符合题意；
B、轴对称图形，故本选项不合题意；
C、是轴对称图形，故本选项不合题意；
D、是轴对称图形，故本选项不合题意．
故选：A．
3. 2024年4月11日华为公司上市的Mate40手机搭载的是自主研发的麒麟处理器，这款处理器是采用制程技术的手机芯片，，其中用科学记数法表示为（ ）
A. B.
C. D.
【答案】D
【解析】，
故选：D．
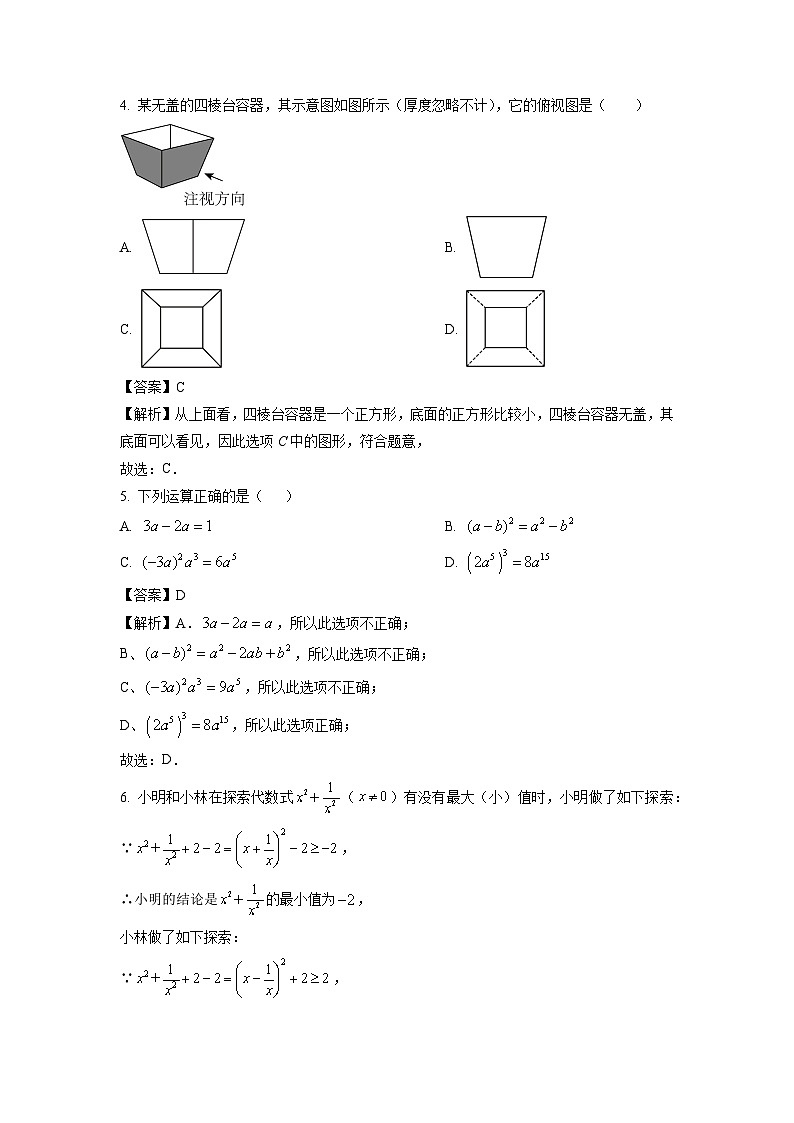
4. 某无盖的四棱台容器，其示意图如图所示（厚度忽略不计），它的俯视图是（ ）
A. B.
C. D.
【答案】C
【解析】从上面看，四棱台容器是一个正方形，底面的正方形比较小，四棱台容器无盖，其底面可以看见，因此选项C中的图形，符合题意，
故选：C．
5. 下列运算正确的是（ ）
A. B.
C. D.
【答案】D
【解析】A．，所以此选项不正确；
B、，所以此选项不正确；
C、，所以此选项不正确；
D、，所以此选项正确；
故选：D．
6. 小明和小林在探索代数式（）有没有最大（小）值时，小明做了如下探索：
∵，
∴小明的结论是的最小值为，
小林做了如下探索：
∵，
小林的结论是的最小值为2；则（ ）
A. 小明正确B. 小林正确
C. 小明和小林都正确D. 小明和小林都不正确
【答案】B
【解析】小明的探究：，
则当，即时，有最小值为，
而无解，
小明的探究是错误的，
小林的探究：，
则当，即时，有最小值为2，
小林的探究是正确的，
故选：B．
7. 已知关于x，y的方程组的解是则关于x，y的方程组的解是（ ）
A. B. C. D.
【答案】B
【解析】∵方程组的解是，
∵方程组可化为，
的解是，即，
故选：B．
8. 如图，是的直径，点C、D、E在上，若，，且，则为（ ）
A. B. 6C. D.
【答案】B
【解析】连接、、，过点作于，如图，
∵为直径，
∵，
∴，
∵，
在中，，
故选：B．
9. 如图，在中，，，，按如下步骤作图：
①分别以点，为圆心，以大于的长为半径在两边作弧，交于两点，；②作直线，分别交，于点，；③过作 交于点，连接，．则四边形的周长为（ ）

A. B. C. D.
【答案】C
【解析】根据作图过程可知：是的垂直平分线，
∴，，
∴，，
∵，
∴，
∴，
∴，
∴四边形是平行四边形，
∴四边形是菱形，
∵，，，
∴，，，
又∵，
∴，即，
∴，
∴点是的中点，
∴是的中位线，
∴，
∴，
∴菱形的周长为．
故选：C．
10. 已知一系列抛物线，，，，，…，（k为非负整数）．抛物线与x轴相交于点，（点在点的左边），顶点为．若轴于点，则k的值是（ ）
A. 3B. 5C. 2023D. 2024
【答案】A
【解析】根据题意可得：的顶点坐标是，
的顶点坐标是，
的顶点坐标是，
的顶点坐标是，
的顶点坐标是，
观察这列抛物线的顶点坐标，
由规律可知的顶点坐标是，
∴抛物线的解析式是，
，
，
轴于点，
，
把点的坐标代入到的解析式得：，
解得：；
故选：A．
二、填空题：本题共6小题，每小题3分，共18分．
11. 分解因式：=______．
【答案】x（x+2）（x﹣2）
【解析】==x（x+2）（x﹣2）．
故答案为：x（x+2）（x﹣2）．
12. 若，且，则a的取值范围是__________．
【答案】
【解析】∵，
∴，
∴，
故答案为：．
13. 若m，n是方程的两个实数根，则__________．
【答案】
【解析】∵m，n是方程的两个实数根，
∴，，
∴，
∴，
∴，
故答案为．
14. 如图，是的外接圆，，，若扇形（图中阴影部分）正好是一个圆锥的侧面展开图，则该圆锥的高为__________．
【答案】
【解析】连接，
，
，
，
，
，
，
，
∴是等边三角形，
，
设扇形围成的圆锥的底面半径为，
则，
解得，
∴该圆锥的高为：，
故答案为：．
15. 如图1，在菱形中，E为的中点，点F沿从点A向点C运动，连接，，设，，图2是点F运动时y随x变化的关系图象，则y的最小值是______．
【答案】
【解析】由函数图象得：当点F与点A重合时；如图，
此时，，
∵ E为的中点，
∴，
∴，
∴，
∴，
当点F与点C重合时；如图，过点E作，垂足为G，设与交于点H，
此时，，
∴，
∵，
∴，
∴，
∴，
∴，
设，则，
在中，，
在中，，即，
解得：，
∴，
∴，
如图，当三点共线时，有最小值，最小值为的长，连接，
∵，E为的中点，
∴，
∴
∴y的最小值是，
故答案为．
16. 如图，E是正方形边上的动点（不与重合），连接交对角线于点F，过点F作交于点G．连接、，则下列结论①；②；③；④；⑤．其中正确的有______．（写出所有正确结论的序号）．
【答案】①④⑤
【解析】如图1，连接，
在正方形中，，
在和中，，
，
，
，
∴在四边形中，，
又∵，∴，
∴，∴，
∴，故①正确；
如图2，把顺时针旋转得到，
则，
，故②错误；
，
，
∴是等腰直角三角形，
，
∴，故③错误；
，
，
在和中，，
，
，
，故④正确；
，
，
，
，
，
，
，
，故⑤正确；
故答案为：①④⑤．
三、解答题：本题共8小题，共72分．解答应写出文字说明、证明过程或推演步骤．
17. （1）计算：；
（2）先化简，再从，0，1，2中选择一个适合的数代入求值．
解：（1）；
（2）原式
，
由原式可知，a不能取，0，
当时，原式（或当时，原式）．
18. 推广体育“大课间”活动，某中学决定开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图①②的统计图．请结合图中的信息解答下列问题：
（1）在这项调查中，共调查了多少名学生？
（2）请计算本项调查中喜欢“立定跳远”的学生人数，并将条形统计图补充完整；
（3）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生．现从这5名学生中任意抽取2名学生．请用画树状图或列表的方法，求出刚好抽到“一男一女”的概率．
解：（1）根据题意得：（名）．
答：在这项调查中，共调查了150名学生．
（2）本项调查中喜欢“立定跳远”的学生人数是：（人），
画图如下：
（3）用A表示男生，B表示女生，画图如下：
共有20种情况，“一男一女”的情况是12种，
（“一男一女”）．
答：刚好抽到“一男一女”的概率是．
19. 某商场准备购一批特色商品，经调查，用16000元采购A商品的件数是用7500元采购B商品的件数的2倍，一件A商品的进价比一件B商品的进价多10元．
（1）求一件A，B商品的进价分别为多少元？
（2）若该商场购进A，B商品共250件进行试销，其中A商品的件数不大于B商品的件数，且不小于20件．A商品的售价与A商品销量之间的关系如下表所示：
B商品的售价降为210元/件，且全部售出．设购进A商品m件，求出这批商品的最大利润，并求出此时的进货方案．
解：（1）设一件B商品的进价为x元，则一件A商品的进价为元．
由题意：，
解得，
经检验是分式方程的解，
，
答：一件A型商品的进价为160元，一件B型商品的进价为150元．
（2）设商场购进A型商品m件，则商场购进B型商品件，
由题意：，解得，，
由表中数据可知，商品A的售价y与销量m是一次函数关系，可设为，
代入两组数据得：，解得，
，
设总利润为w元，根据题意得，
，
，
当时，w随m的增大而减小，
，
当时，w有最大值为，
答：这批商品的最大利润为14600元，此时的进货方案是A商品进20件，商品进货230件．
20. 直线分别与轴，轴交于点、，与反比例函数的图象交于点、．
（1）求的值及直线的解析式；
（2）连接，若在射线上存在点，使，求点的坐标；
（3）如图2，将反比例函数的图象沿直线翻折得到一个封闭图形（图中阴影部分），若直线与此封闭图形有交点，请直接写出满足条件的的取值范围．
解：（1）点在反比例函数，
将点的坐标代入，得，，
反比例函数为，
又在反比例函数，
，即，
点，在直线上
，
直线的解析式为；
（2）直线为，．
，
，
设，
如图，在射线上，此时可得必在轴负半轴，，
．
，
．
∴；
（3）依据题意，直线平行于直线，且与轴交于点E，则
与封闭图形有交点，下端与相切于点，上端相切于翻折后的曲线于点，
由题意，，
．
相切，
判别式．
（负数舍去）．
此时．与轴的交点为，，
，
，
，，
此时．与轴的交点为，
．
21. 交通安全心系千万家，高速公路管理局在某隧道内安装了测速仪，如图所示的是该段隧道的截面示意图．测速仪和测速仪到路面之间的距离，测速仪和之间的距离，一辆小汽车在水平的公路上由西向东匀速行驶，在测速仪处测得小汽车在隧道入口点的俯角为，小汽车到测速仪的水平距离，在测速仪处测得小汽车在点的俯角为，小汽车在隧道中从点行驶到点所用的时间为（图中所有点都在同一平面内）．
（1）求，两点之间的距离（结果精确到）；
（2）若该隧道限速，判断小汽车从点行驶到点是否超速？通过计算说明理由．
（参考数据：，，，，，，）
解：（1）由题意得：，，米，
在中，米，
∴米，
在中，米，
∴（米），
∴（米），
∴，两点之间的距离约为760米．
（2）小汽车从点行驶到点没有超速．
理由：由题意得：
米/秒，
∵20米/秒<22米/秒，
∴小汽车从点行驶到点没有超速．
22. 如图1，在中，，点D为边中点，点E为线段上一动点，过点A，D，E作分别交，于点F，G，连接，．
（1）求证：；
（2）已知：，，当四边形为平行四边形时，请补全图2，并求出的长．
（1）证明：如图，连接，
，点D为边中点，
，
，
，
，
；
（2）解：补全图形如图，连接，，
四边形为平行四边形，
，
，
，
，
为的直径，
，
，
，
，
，
在中，，
．
23. 如图，已知抛物线的图象经过点D，，C是的中点，P是拋物线上的一个动点，连接，设点P的横坐标为n．
（1）求抛物线的表达式；
（2）若点P在x轴上方的拋物线上运动，连接，当四边形面积最大时，求n的值；
（3）如图，若点Q在坐标轴上，是否存在点Q，使，若存在，直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．
解：（1）∵，
∴，
∵，
∴．
∵是的中点，
∴．
∵在的图象上，
，
得，
．
（2）过作x轴垂线交于，
设直线，即，解得：，
故解析式为：，
由， 得，
，
，
当四边形面积最大时，．
（3）①当点Qy轴上时，使，
∵，
即，
∴，
∴，
过点D作轴交y轴于点H，
则，
∵，
∴，
∴，
∴，
根据（1）得，
∴，
∴点Q的坐标为；
②当点Q在x轴上时，使，
延长交x轴于点F，过点D作轴交x轴于点G，
则，
则 ，，
∴，
，
，
，
，
，
，
，
，
即，
，
，
∴点的坐标为，
综上，或．
24. 小东在学习过程中，注重知识的迁移和延伸，下面是他在“图形的旋转”主题下设计的问题，请你解答．
（1）操作发现
如图1，在中，，，点是边上一动点（不与点，重合），连接，将线段绕点逆时针旋转，得到线段，连接，，则______；若点，分别是，中点，则，之间的数量关系为_____．
（2）迁移应用
如图2，在中，，，于点，点是线段上一动点（不与点，重合），将线段绕点顺时针旋转，得到线段．点在线段上，且．猜想，之间的位置关系，并就图2所示的情形给出证明．
（3）问题解决
在（2）的条件下，若，，当是直角三角形时，请直接写出的长．
解：（1）∵将线段绕点逆时针旋转，
∴，，
∵，
∴，
即，
∵，
∴，
∴，，
∵，，
∴，
∴，
∵点，分别是，的中点，
∴，
∴，
故答案为：，；
（2）如图，延长至点，使，连接，，，
∵，
∴，，
∴，
∵，，
∴，
∴，
∴，
∵，，
∴，
∵，，
∴，
∴，
∴，
∴，
∵，
∴；
（3）∵，，
∴，
∴，
根据题意是直角三角形分三种情况：
情况①：当时，如图，
由（2）可得，
∴，
∴，
即是等腰直角三角形，
与，矛盾，
故不存在；
情况②：当时，如图，
∵，
∴、、共线，
∵，
∴，
∵，，
∴，
∴，
∵，，
∴，
∴，
设，
∴，，
∴，
解得：，
即；
情况③：当时，如图，
∵，
∴四边形为矩形，
∴，，
由（2）知，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
∴．
综上，当是直角三角形时，的长为或．A型商品的销量（件）
0
5
10
15
20
…
A型商品的售价（元/件）
240
230
220
210
200
…