数学：山东省济宁市北湖区2023-2024学年七年级下学期期中考试试题（解析版）

这是一份数学：山东省济宁市北湖区2023-2024学年七年级下学期期中考试试题（解析版），共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
第I卷（共30分）
一、单选题（每小题3分，共30分）
1. 下列各式中属于二元一次方程的有（ ）
①；②；③；④；⑤；⑥；
⑦．
A. 2个B. 3个C. 4个D. 5个
【答案】C
【解析】根据定义可知①②③是二元一次方程，④中未知数项次数是2次，而不是1次，它不是二元一次方程；⑤是代数式，不是方程；⑥是分式方程，⑦整理后为，是二元一次方程．故正确的有①②③⑦，共4个，
故选：．
2. 下列事件是必然事件是（ ）
A. 车辆随机到达一个路口遇到红灯
B. 早上的太阳从西方升起
C. 400人中至少有两人的生日在同一天
D. 投掷一枚质地均匀的硬币，正面朝上
【答案】C
【解析】选项A，是随机事件，不是必然事件，不符合题意；
选项B，是不可能事件，不是必然事件，不符合题意；
选项C，是必然事件，符合题意；
选项D，是随机事件，不是必然事件，不符合题意．
故选C．
3. 下列命题是真命题的是（ ）
A. 相等的角是对顶角．B. 若数满足，则
C. 两条直线被第三条直线所截，同位角相等D. 垂线段最短
【答案】D
【解析】A、相等的角不一定是对顶角，故原命题错误，是假命题，不符合题意；
B、若数a、b满足，则或，故原命题错误，是假命题，不符合题意；
C、两条平行直线被第三条直线所截，同位角相等，故原命题错误，是假命题，不符合题意；
D、垂线段最短，故原命题正确，符合题意；
故选：D．
4. 不透明的袋子里装有8个小球，其中5个红色，3个蓝色，则下列说法不正确的是（ ）
A. 从中随机抽取1个球，抽到红色的可能性更大
B. 从中随机抽取1个球，抽到红色和蓝色的可能性一样大
C. 从中随机抽取6个球，一定有蓝色的
D. 从中随机抽取5个球，可能都是红色的
【答案】B
【解析】A．从中随机抽取1个球，抽到红球的概率为，抽到蓝球的概率为，结论正确，不符合题意；
B．从中随机抽取1个球，抽到红球的概率为，抽到蓝球的概率为，结论错误，符合题意；
C．因为只有个红球，所以从中随机抽取6个球，至少有个是蓝色的，结论正确，不符合题意；
D．从中随机抽取5个球，可能都是红色的，结论正确，不符合题意；
故选：B．
5. 如图，直线与相交于点，则关于的方程的解是（ ）
A. B. C. D.
【答案】C
【解析】∵直线与相交于点，
∴，
∴，
∴，
∴结合图象，关于的方程的解是，
故选：C．
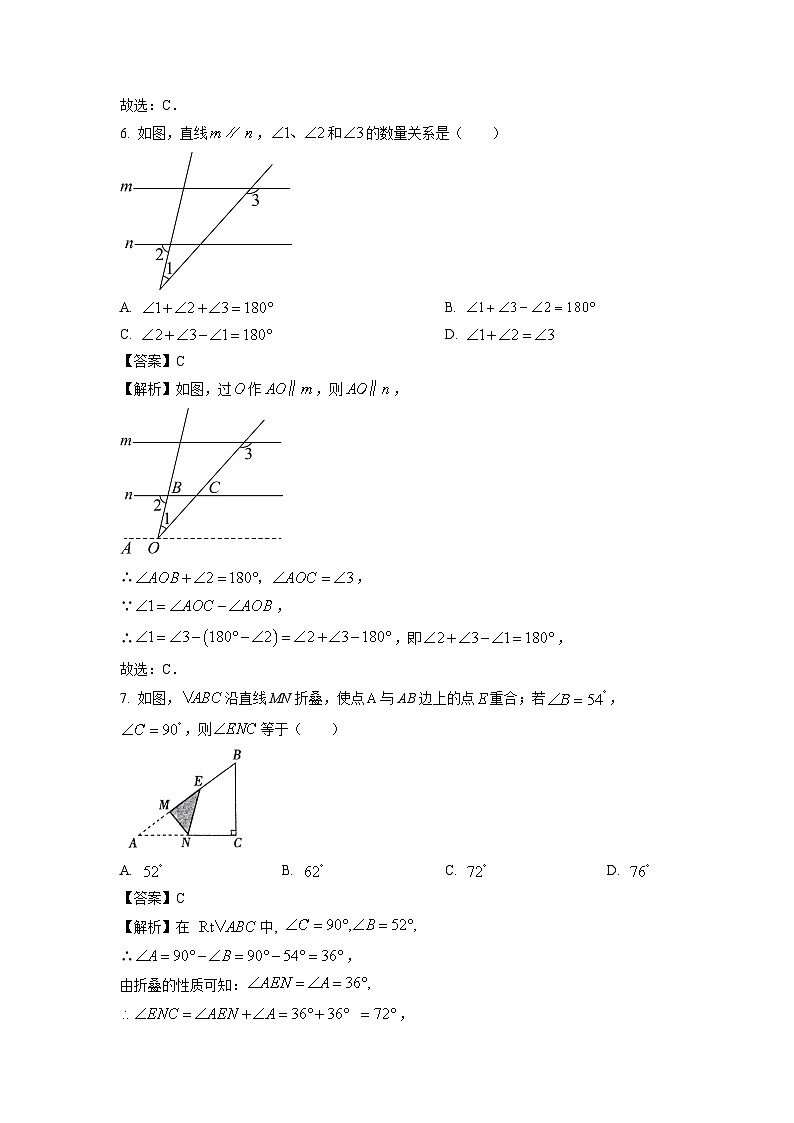
6. 如图，直线，和的数量关系是（ ）

A. B.
C. D.
【答案】C
【解析】如图，过作，则，

∴，
∵，
∴，即，
故选：C．
7. 如图，沿直线MN折叠，使点与AB边上的点重合；若，，则等于（ ）
A. B. C. D.
【答案】C
【解析】在 中,
∴，
由折叠的性质可知：
，
故选: C.
8. 某校学生去参加活动，若单独调配30座(不含司机)客车若干辆，则有5人没有座位；若只调配25座(不含司机)客车，则用车数量将增加3辆，并空出5个座位．设计划调配30座客车辆，该大学共有名大学生志愿者，则下列方程组正确的是（ ）
A. B.
C. D.
【答案】B
【解析】设计划调配30座客车辆，则只调配25座(不含司机)客车时，用车数量为辆，
由此列方程组．
故选：B．
9. 在长方形中，放入5个形状大小相同的小长方形（空白部分），其中，，则阴影部分图形的总面积为（ ）．
A. 27B. 29C. 34D. 36
【答案】A
【解析】设小长方形的长为，宽为，
根据题意，得：，
解得：，
∴每个小长方形的面积为，
∴阴影部分的面积．
故选：A．
10. 如图，，分别平分．以下结论，其中正确的是（ ）
①；②；
③；④．
A. ①②B. ②③④C. ①③④D. ①②③④
【答案】D
【解析】∵平分，
∴，
∵是的一个外角，
∴，
∵，
∴，
∴，
∵，
∴，故①正确；
∴，
∵平分，
，
，即，故②正确；
∵平分，
，
∵是的一个外角，
∴，
∵是的一个外角，
∴
，
∴，故③正确；
∵，
∴，
∴，
∵，，
∴，
∵，
∴，
∴，故④正确；
∴以上结论正确的是①②③④，
故选：D．
第II卷（共70分）
二、填空题（每小题3分，共15分）
11. 对顶角相等．这个命题的条件是________________．
【答案】两个角是对顶角
【解析】 “对顶角相等”改写为：如果两个角是对顶角，那么这两个角相等，
∴“对顶角相等”的条件是：两个角是对顶角，结论是：这两个角相等，
故答案为：两个角是对顶角．
12. 从一组数，，，0，1，2，3中随机选一个数，恰好是非负数的概率为______．
【答案】
【解析】∵均为非负数，∴随机选一个数，恰好是非负数的概率为：，
故答案为：.
13. 如图，把一张长方形纸片沿折叠后，点A落在边上的点处，点B落在点处，与交于点G，若，则的度数为________________．
【答案】
【解析】由折叠与长方形可知，，，
∴，
∵，
∴，
∵，
∴，
故答案为：．
14. 若方程组的解是，则方程组的解是_____．
【答案】
【解析】∵方程组的解是，
∴，解得，
故答案为：．
15. 如图，在中，为的外角，与的平分线交于点与的平分线交于点与的平分线相交于点，当两条角平分线无交点时，则的值为_______________．
【答案】3
【解析】，，
，
又 和 分别平分和,
,,
，
，
和 分别平分 和
，
，

，
，
同理可得，
，
，
，
∴无法组成三角形，即两条角平分线无交点，
故的值为.
三、解答题（共7题，共55分）
16. 解方程组．
解：方程组，
得：，
解得，
将代入①式得：，
解得，
故方程组的解为：．
17. 请把下列证明过程补充完整．
已知：如图，B、C、E三点在同一直线上，A、F、E三点在同一直线上，，，求证：．
证明∶ ∵（已知），
∴________（______），
∴____（______），
∵（已知），
∴____（等量代换），
∵（已知），
∴，即，
∴____（等量代换），
∴（_____）．
证明： ∵（已知），
∴（内错角相等，两直线平行），
∴（两直线平行，内错角相等），
∵（已知），
∴（等量代换），
∵（已知），
∴，即，
∴（等量代换），
∴（同位角相等，两直线平行）．
18. 一个不透明的袋中有红、黄、白三种颜色球共50个，它们除了颜色外其他都相同，其中黄球个数比白球个数的2倍少5个，已知从袋中摸出一个红球的概率是．
（1）求袋中白球的个数；
（2）求从袋中摸出一个球是黄球的概率；
（3）取走2个白球和3个黄球后，求从剩余的球中摸出一个球是红球的概率．
解：（1）袋中红球的个数为（个），
则袋中黄、白球的总个数为（个），
设袋中白球的个数为x个，
则，
解得，
∴袋中白球有15个；
（2）由（1）知，袋中黄球的个数为个，
所以从袋中摸出一个球是黄球的概率为；
（3）取走2个白球和3个黄球后，红球有10个，球的总个数为45个，
所以从剩余的球中摸出一个球是红球的概率为．
19. 如图，在中，分别平分，且交于点O，为外角的平分线，交的延长线于点E．记，已知．求与的度数．
解：为的平分线，平分，
，．
是的外角，是的外角，
，
．
平分，平分，，，
，
是的外角，
．
20. 某生态体验园推出了甲，乙两种消费卡，设入园次数为次，所需费用为y元，选择这两种卡消费时，y与x的函数关系如图所示，解答下列问题：
（1）分别求出选择这两种卡消费时，关于的函数表达式；
（2）当消费多少次时，甲，乙两种消费卡的费用相同？
解：（1）设，把代入得，
解得，．
设，把代入得，
解得，；
（2）联立，解得，，
所以，当入园次数等于10时，选择两种消费卡费用一样．
21. 某医药公司销售甲、乙两种型号的口罩共20万只，其中成本、售价如表：
（1）当所有口罩全部销售时，该公司可获利润8.8万元，求该公司销售甲、乙两种型号的口罩分别是多少万只？
（2）小明有16.2元的零花钱，打算购买甲和乙两种口罩(两种都要买)，正好赶上口罩价格调整，其中甲型口罩售价上涨50%，乙型口罩按原价出售，则小明有多少种不同的购买方案可以使钱正好花完？请设计出这些方案．
解：（1）设甲型号口罩生产x万只，乙型口罩生产了y万只，
由题意可得：，
解得：，
答：甲型号口罩生产12万只，乙型口罩生产了8万只；
（2）设该同学购买只甲型口罩，只乙型口罩，
根据题意得：，
．
又，均为正整数，
或，
该同学共有2种购买方案，
方案1：购买4个甲型口罩，9个乙型口罩；
方案2：购买2个甲型口罩，18个乙型口罩．
22. 点在射线上，点、为射线上两个动点，满足，，平分．
（1）如图，当点在右侧时，求证：；
（2）如图，当点在左侧时，求证：；
（3）如图，在（2）的条件下，为延长线上一点，平分，交于点，平分，交于点，连接，若，，则的度数是多少．
解：（1）平分，
，
又，
，
∴，
，
，
，
∴；
（2）过点作，交于点，如图，
由（1）同理可证：，
，
，，
，
；
（3）设，
则，，
，
平分，
，
，
，
，
，
，
，
，
，
，
解得：，
．甲
乙
成本
1.2元/只
0.4元/只
售价
1.8元/只
0.6元/只