
高考数学复习第九章 第七节 抛物线(导学案)
展开1.了解抛物线的定义、几何图形和标准方程,以及它们的几何性质.
2.通过抛物线与方程的学习,进一步体会数形结合思想.
3.了解抛物线的简单应用.
1.抛物线的定义
满足以下三个条件的点的轨迹是抛物线:
(1)在平面内;
(2)动点到定点F的距离与到定直线l的距离相等;
(3)定点不在定直线上.
其中点F叫做抛物线的焦点,直线l叫做抛物线的准线.
点睛 若定点F在定直线l上,则动点的轨迹为过点F且垂直于l的一条直线.
2.抛物线的标准方程和几何性质
点睛 四种不同抛物线方程的共同点
(1)原点都在抛物线上;
(2)焦点都在坐标轴上;
(3)准线与焦点所在坐标轴垂直,垂足与焦点关于原点对称,它们与原点的距离都等于一次项系数的绝对值的 eq \f(1,4) ,即 eq \f(2p,4) = eq \f(p,2) .
抛物线y2=2px(p>0)的焦点为F,AB是其过焦点的弦,A(x1,y1),B(x2,y2),则
1.|AB|=x1+x2+p.
2. eq \f(1,|AF|) + eq \f(1,|BF|) = eq \f(2,p) .
3.x1x2= eq \f(p2,4) ,y1y2=-p2.
4.以抛物线焦点弦为直径的圆与准线相切.
5.过抛物线焦点弦的两端点向准线作垂线,以两垂足为直径端点的圆与焦点弦相切.
1.(教材变式)抛物线y2=x的准线方程是( )
A.x=- eq \f(1,2) B.x=- eq \f(1,4)
C.y=- eq \f(1,2) D.y=- eq \f(1,4)
解析:选B.由抛物线方程y2=x可知2p=1,p= eq \f(1,2) ,故准线方程为x=- eq \f(p,2) =- eq \f(1,4) .
2.(弄错焦点位置)抛物线x2=2py(p>0)上纵坐标为2的点到焦点的距离为5,则该抛物线的方程为( )
A.x2=12y B.x2=10y
C.x2=8y D.x2=6y
解析:选A.因为抛物线x2=2py(p>0)上纵坐标为2的点到焦点的距离为5,
则根据抛物线的定义可得2+ eq \f(p,2) =5,解得p=6,
所以抛物线的方程为x2=12y.
3.(教材提升)抛物线x2=4y上一点A(2 eq \r(2) ,2)到焦点的距离为________.
解析:因为点A(2 eq \r(2) ,2)在该抛物线上,且抛物线的准线方程为y=-1,
所以点A(2 eq \r(2) ,2)到焦点的距离为2-(-1)=3.
答案:3
4.(不会应用抛物线定义)拋物线C:y2=2px(p>0)的焦点为F,点P(2,m)为C上一点,若 eq \b\lc\|\rc\|(\a\vs4\al\c1(PF)) =3,则m=__________.
解析:拋物线C:y2=2px的准线方程为x=- eq \f(p,2) ,
因为 eq \b\lc\|\rc\|(\a\vs4\al\c1(PF)) =3,所以2-(- eq \f(p,2) )=3⇒p=2,把P(2,m)代入抛物线方程中,得m2=2×2×2⇒m=±2 eq \r(2) .
答案:±2 eq \r(2)
5.(结论1)斜率为 eq \r(3) 的直线过抛物线C:y2=4x的焦点,且与C交于A,B两点,则|AB|=________.
解析:因为抛物线的方程为y2=4x,
所以抛物线的焦点F的坐标为(1,0),
又因为直线AB过焦点F且斜率为 eq \r(3) ,
所以直线AB的方程为y= eq \r(3) (x-1),
代入抛物线方程消去y并化简得3x2-10x+3=0,
方法一:解得x1= eq \f(1,3) ,x2=3,
所以|AB|= eq \r(1+k2) |x1-x2|= eq \r(1+3) ·|3- eq \f(1,3) |= eq \f(16,3) .
方法二:Δ=100-36=64>0,
设A(x1,y1),B(x2,y2),则x1+x2= eq \f(10,3) ,
过A,B分别作准线x=-1的垂线,设垂足分别为C,D,如图所示.
|AB|=|AF|+|BF|=|AC|+|BD|=x1+1+x2+1=x1+x2+2= eq \f(16,3) .
答案: eq \f(16,3)
抛物线的定义及标准方程
[典例1](1)设抛物线的顶点为O,焦点为F,准线为l.P是抛物线上异于O的一点,过P作PQ⊥l于Q,则线段FQ的垂直平分线( )
A.经过点O B.经过点P
C.平行于直线OP D.垂直于直线OP
解析:选B.如图所示,因为线段FQ的垂直平分线上的点到F,Q的距离相等,又点P在抛物线上,根据定义可知, eq \b\lc\|\rc\|(\a\vs4\al\c1(PQ)) = eq \b\lc\|\rc\|(\a\vs4\al\c1(PF)) ,所以线段FQ的垂直平分线经过点P.
(2)(2023·岳阳模拟)已知抛物线y= eq \f(1,4) x2的焦点为F,P为抛物线上一动点,点Q(1,1),当△PQF的周长最小时,点P的坐标为________.
解析:如图,设l:y=-1是抛物线的准线,过P作PH⊥l于H,作QN⊥l于N,
则 eq \b\lc\|\rc\|(\a\vs4\al\c1(PF)) = eq \b\lc\|\rc\|(\a\vs4\al\c1(PH)) ,F(0,1), eq \b\lc\|\rc\|(\a\vs4\al\c1(FQ)) =1,
eq \b\lc\|\rc\|(\a\vs4\al\c1(PF)) + eq \b\lc\|\rc\|(\a\vs4\al\c1(PQ)) = eq \b\lc\|\rc\|(\a\vs4\al\c1(PQ)) + eq \b\lc\|\rc\|(\a\vs4\al\c1(PH)) ,
易知当Q,P,H三点共线时, eq \b\lc\|\rc\|(\a\vs4\al\c1(PQ)) + eq \b\lc\|\rc\|(\a\vs4\al\c1(PH)) 的值最小,且最小值为1+1=2,所以△PQF的周长最小值为3,此时xP=1,yP= eq \f(1,4) ,即P(1, eq \f(1,4) ).
答案:(1, eq \f(1,4) )
1.抛物线定义的应用
利用抛物线的定义解决问题时,应灵活地进行抛物线上的点到焦点距离与其到准线距离间的等价转化.
2.求抛物线的标准方程的方法
(1)定义法.
根据抛物线的定义,确定p的值(系数p是指焦点到准线的距离),再结合焦点位置,求出抛物线方程.
(2)待定系数法.
①根据抛物线焦点是在x轴上还是在y轴上,设出相应形式的标准方程,然后根据条件确定关于p的方程,解出p,从而写出抛物线的标准方程.
②当焦点位置不确定时,有两种方法解决:
1.(2022·惠州模拟)若抛物线y2=2px(p>0)上一点P(2,y0)到其焦点的距离为4,则抛物线的标准方程为( )
A.y2=2x B.y2=4x
C.y2=6x D.y2=8x
解析:选D.抛物线y2=2px上一点P(2,y0)到焦点的距离等于到其准线的距离,即为4,所以 eq \f(p,2) +2=4,解得p=4,所以抛物线的标准方程为y2=8x.
2.(2023·福州模拟)已知抛物线C:y2=4x的焦点为F,准线为l,点P在C上,直线PF与y轴交于点M,且 eq \(PF,\s\up6(→)) =2 eq \(FM,\s\up6(→)) ,则点P到准线l的距离为( )
A.3 B.4 C.5 D.6
解析:选B.如图,过点P作y轴的垂线,垂足为N,由题知F(1,0),即 eq \b\lc\|\rc\|(\a\vs4\al\c1(OF)) =1,
因为 eq \(PF,\s\up6(→)) =2 eq \(FM,\s\up6(→)) ,
所以 eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(\(MF,\s\up6(→)))),\b\lc\|\rc\|(\a\vs4\al\c1(\(MP,\s\up6(→))))) = eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(OF)),\b\lc\|\rc\|(\a\vs4\al\c1(PN))) = eq \f(1,3) ,
所以 eq \b\lc\|\rc\|(\a\vs4\al\c1(PN)) =3,所以点P到准线l的距离为 eq \b\lc\|\rc\|(\a\vs4\al\c1(PN)) +1=4.
3.(2022·大连模拟)已知抛物线C:y2=8x的焦点为F,在C上有一点P,|PF|=8,则点P到x轴的距离为________.
解析:由抛物线的定义可知, eq \b\lc\|\rc\|(\a\vs4\al\c1(PF)) =xp+2=8,
所以xp=6,代入y2=8x中,得y eq \\al(\s\up1(2),\s\d1(p)) =48,
所以 eq \b\lc\|\rc\|(\a\vs4\al\c1(yp)) =4 eq \r(3) ,故点P到x轴的距离为4 eq \r(3) .
答案:4 eq \r(3)
【加练备选】
设抛物线C:y2=4x的焦点为F,点P为C上的任意点,若点A使得|AP|+|PF|的最小值为4,则下列选项中,符合题意的点A为( )
A.(4,2) B.(4,4)
C.(3,3) D.(3,4)
解析:选C.抛物线的准线方程为x=-1,焦点坐标为(1,0),
A:因为A(4,2)在抛物线内部,而A(4,2)到准线的距离为4-(-1)=5,所以|AP|+|PF|的最小值为5,不符合题意;
B:因为A(4,4)在抛物线上,所以|AP|+|PF|的最小值就是|AF|= eq \r((4-1)2+(4-0)2) =5,不符合题意;
C:因为A(3,3)在抛物线内部,A(3,3)到准线的距离为:3-(-1)=4,
所以|AP|+|PF|的最小值为4,符合题意;
D:因为A(3,4)在抛物线外部,
所以|AP|+|PF|的最小值就是|AF|= eq \r((3-1)2+(4-0)2) =2 eq \r(5) ,不符合题意.
抛物线的几何性质
[典例2](1)(2023·烟台模拟)已知点F为抛物线y2=2px(p>0)的焦点,点P在抛物线上且横坐标为8,O为坐标原点,若△OFP的面积为2 eq \r(2) ,则该抛物线的准线方程为( )
A.x=- eq \f(1,2) B.x=-1
C.x=-2 D.x=-4
解析:选B.抛物线y2=2px(p>0)的焦点F( eq \f(p,2) ,0),
由y2=16p,可得y=±4 eq \r(p) ,不妨令P(8,4 eq \r(p) ),
则S△OFP= eq \f(1,2) × eq \f(p,2) ×4 eq \r(p) =p eq \r(p) =2 eq \r(2) ,解得p=2,则抛物线方程为y2=4x,其准线方程为x=-1.
(2)(2021·新高考Ⅰ卷)已知O为坐标原点,抛物线C:y2=2px(p>0)的焦点为F,P为C上一点,PF与x轴垂直,Q为x轴上一点,且PQ⊥OP.若|FQ|=6,则C的准线方程为____________.
解析:由已知可设P eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2),p)) ,所以kOP=2,kPQ=- eq \f(1,2) ,
因此直线PQ的方程为y-p=- eq \f(1,2) eq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(p,2))) ,
令y=0得x= eq \f(5p,2) ,因此|FQ|= eq \f(5p,2) - eq \f(p,2) =2p=6,则p=3,
所以C的准线方程为x=- eq \f(p,2) =- eq \f(3,2) .
答案:x=- eq \f(3,2)
用抛物线几何性质的技巧
涉及抛物线几何性质的问题常结合图形思考,通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征,体现了数形结合的思想.
1.(2021·新高考Ⅱ卷)若抛物线y2=2px(p>0)的焦点到直线y=x+1的距离为 eq \r(2) ,则p=( )
A.1 B.2 C.2 eq \r(2) D.4
解析:选B.抛物线的焦点坐标为 eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2),0)) ,
其到直线x-y+1=0的距离d= eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(\f(p,2)-0+1)),\r(1+1)) = eq \r(2) ,
解得p=2(p=-6舍去).
2.(2022·潍坊模拟)抛物线C:x2=4ay的焦点坐标为(0,2),则C的准线方程为________.
解析:因为抛物线C:x2=4ay的焦点坐标为(0,2),所以C的准线方程为y=-2.
答案:y=-2
3.(2023·佛山模拟)抛物线y2=2px(p>0)上一点M(3,t)与焦点F的距离|MF|=p,则M到坐标原点的距离为____________.
解析:抛物线y2=2px的准线为x=- eq \f(p,2) ,
由抛物线定义得:3-(- eq \f(p,2) )=p,解得p=6,
抛物线方程为y2=12x,而M(3,t)在抛物线上,
则t2=36,原点为O,即有|MO|= eq \r(32+t2) =3 eq \r(5) ,
所以M到坐标原点的距离为3 eq \r(5) .
答案:3 eq \r(5)
【加练备选】
(2022·泉州模拟)抛物线具有如下光学性质:从焦点发出的光线经过抛物线上的一点反射后,反射光线平行于抛物线的对称轴.生活中的探照灯就是利用这个原理设计的.已知F是抛物线C:y2=4x的焦点,从F发出的光线经C上的点M反射后经过点(4,2 eq \r(3) ),则|FM|=( )
A.2 B.3 C.4 D.5
解析:选C.因为从F发出的光线经C上的点M反射后经过点(4,2 eq \r(3) ),
由抛物线的光学性质可知yM=2 eq \r(3) .
代入y2=4x得xM=3,又抛物线的准线为x=-1,所以 eq \b\lc\|\rc\|(\a\vs4\al\c1(FM)) =3+1=4.
直线与抛物线的位置关系
角度1 抛物线的焦点弦问题
[典例3](1)设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
A.y2=±4x B.y2=±8x
C.y2=4x D.y2=8x
解析:选B.抛物线y2=ax(a≠0)的焦点F坐标为 eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(a,4),0)) ,则直线l的方程为y=2 eq \b\lc\(\rc\)(\a\vs4\al\c1(x-\f(a,4))) ,它与y轴的交点为A eq \b\lc\(\rc\)(\a\vs4\al\c1(0,-\f(a,2))) ,
所以△OAF的面积为 eq \f(1,2) · eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(a,4))) · eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(a,2))) =4,解得a=±8.
所以抛物线方程为y2=±8x.
(2)过抛物线y2=2px(p>0)的焦点F作倾斜角为45°的直线交抛物线于A,B两点,若线段AB的长为8,则p=________.
解析:由题意可知过焦点的直线方程为y=x- eq \f(p,2) .联立抛物线与直线方程 eq \b\lc\{(\a\vs4\al\c1(y2=2px,,y=x-\f(p,2))) ⇒x2-3px+ eq \f(p2,4) =0,设A(x1,y1),B(x2,y2),
又|AB|=x1+x2+p=3p+p=8⇒p=2.
答案:2
关于焦点弦的几个常用技巧
1.过抛物线y2=2px的焦点的直线方程常设为x=my+ eq \f(p,2) .
2.抛物线的焦点弦长为 eq \f(2p,sin2θ) (θ为过焦点的直线的倾斜角),最小值为2p.
3.过抛物线的焦点弦的两个端点作抛物线的切线,两条切线的交点在准线上.
角度2 直线与抛物线的综合
[典例4](1)(2022·全国乙卷)设F为抛物线C:y2=4x的焦点,点A在C上,点B(3,0),若|AF|=|BF|,则|AB|=( )
A.2 B.2 eq \r(2) C.3 D.3 eq \r(2)
解析:选B.由题意得,F(1,0),则|AF|=|BF|=2,
即点A到准线x=-1的距离为2,所以点A的横坐标为-1+2=1,
不妨设点A在x轴上方,代入得,A(1,2),
所以|AB|= eq \r((3-1)2+(0-2)2) =2 eq \r(2) .
(2)(2022·德州模拟)已知抛物线x2=2py(p>0)的焦点为F,O为坐标原点,A(t,1)是抛物线第一象限上的点,|AF|=5,直线AF与抛物线的另一个交点为B,则S△AOB=__________.
解析:因为 eq \b\lc\|\rc\|(\a\vs4\al\c1(AF)) =1+ eq \f(p,2) =5,则p=8,
所以抛物线方程为x2=16y,
把A(t,1)代入抛物线方程得:t2=16且t>0,则t=4,
因为A(4,1),F(0,4),则直线AF的斜率k= eq \f(1-4,4-0) =- eq \f(3,4) ,
所以直线AF的方程为y=- eq \f(3,4) x+4,即3x+4y-16=0,
联立方程
解得 eq \b\lc\{(\a\vs4\al\c1(x=4,y=1)) 或 eq \b\lc\{(\a\vs4\al\c1(x=-16,y=16)) ,即B(-16,16),
则 eq \b\lc\|\rc\|(\a\vs4\al\c1(AB)) = eq \r((-16-4)2+(16-1)2) =25,
O到直线AF:3x+4y-16=0的距离d= eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(-16)),\r(32+42)) = eq \f(16,5) ,
所以S△AOB= eq \f(1,2) eq \b\lc\|\rc\|(\a\vs4\al\c1(AB)) ×d=40.
答案:40
1.直线与抛物线的弦长问题
注意直线是否过抛物线的焦点.若过抛物线的焦点,可直接使用公式|AB|=x1+x2+p;若不过焦点,则必须用一般弦长公式.
2.涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系采用“设而不求”“整体代入”等解法.
提醒 涉及弦的中点、斜率时一般用“点差法”求解.
1.(多选题)(2023·盐城模拟)已知抛物线C:y2=2px(p>0)的焦点为F,过F的直线l交抛物线C于点A,B,且A( eq \f(p,4) ,a), eq \b\lc\|\rc\|(\a\vs4\al\c1(AF)) = eq \f(3,2) .下列结论正确的是( )
A.p=4
B.a=± eq \r(2)
C. eq \b\lc\|\rc\|(\a\vs4\al\c1(BF)) =3
D.△AOB的面积为 eq \f(3\r(2),2)
解析:选BCD.选项A,由抛物线的定义可得 eq \b\lc\|\rc\|(\a\vs4\al\c1(AF)) =xA+ eq \f(p,2) = eq \f(p,4) + eq \f(p,2) = eq \f(3,2) ,解得p=2,所以A不正确;
选项B,因为p=2,所以A( eq \f(1,2) ,a),F(1,0),抛物线方程为y2=4x,将点A( eq \f(1,2) ,a)的坐标代入抛物线方程,得a2=4× eq \f(1,2) =2,所以a=± eq \r(2) ,所以B正确;
选项C,当a= eq \r(2) 时,则kl= eq \f(\r(2)-0,\f(1,2)-1) =-2 eq \r(2) ,则直线l的方程为y=-2 eq \r(2) (x-1),
则 eq \b\lc\{(\a\vs4\al\c1(y=-2\r(2)(x-1),y2=4x)) ,得8x2-20x+8=0,解得x1= eq \f(1,2) 或x2=2,所以xB=2,则 eq \b\lc\|\rc\|(\a\vs4\al\c1(BF)) =xB+ eq \f(p,2) =2+1=3,
同理当a=- eq \r(2) 时,可得 eq \b\lc\|\rc\|(\a\vs4\al\c1(BF)) =3,所以C正确;
选项D,由上可知当a= eq \r(2) 时,A( eq \f(1,2) , eq \r(2) ),B(2,-2 eq \r(2) ),
S△AOB=S△AOF+S△BOF
= eq \f(1,2) |OF||yA|+ eq \f(1,2) |OF||yB|
= eq \f(1,2) eq \b\lc\|\rc\|(\a\vs4\al\c1(OF)) · eq \b\lc\|\rc\|(\a\vs4\al\c1(y1-y2))
= eq \f(1,2) ×1×3 eq \r(2) = eq \f(3\r(2),2) ,
同理当a=- eq \r(2) 时,S△AOB= eq \f(3\r(2),2) ,所以D正确.
2.以抛物线C:y2=2px(p>0)的焦点F为端点的一条射线交抛物线于点A,交y轴于点B,若|AF|=2,|BF|=3,则p=____________.
解析:依题意可得F( eq \f(p,2) ,0),设A(x1,y1),则|AF|=x1+ eq \f(p,2) =2,
因为|AF|=2,|BF|=3,所以|AB|=|BF|-|AF|=3-2=1,所以 eq \f(|AB|,|BF|) = eq \f(1,3) ,
又 eq \f(|AB|,|BF|) = eq \f(x1,\f(p,2)) = eq \f(2x1,p) ,所以 eq \f(2x1,p) = eq \f(1,3) ,所以p=6x1,
所以x1+ eq \f(6x1,2) =2,解得x1= eq \f(1,2) ,所以p=6x1=6× eq \f(1,2) =3.
答案:3
【加练备选】
已知抛物线C:y2=4x,O为坐标原点.若存在过点M(m,0)(m>0)的直线l与C相交于A,B两点,且|AM|·|MB|=|OM|2,则实数m的取值范围为( )
A.[4,+∞) B.(0,4)
C.[ eq \f(4,3) ,+∞) D.(0, eq \f(4,3) )
解析:选A.设A(x1,y1),B(x2,y2), eq \(MB,\s\up6(→)) =λ eq \(AM,\s\up6(→)) (λ>0),
则 eq \(AM,\s\up6(→)) =(m-x1,-y1), eq \(MB,\s\up6(→)) =(x2-m,y2),
所以 eq \b\lc\{(\a\vs4\al\c1(x2-m=λ(m-x1),y2=-λy1)) ,①
因为点A,B在抛物线C上,
所以y eq \\al(\s\up1(2),\s\d1(1)) =4x1,y eq \\al(\s\up1(2),\s\d1(2)) =4x2,②
由①②消去x2,y1,y2得λx1=m,
因为|AM|·|MB|=|OM|2,
即|OM|2=λ|AM|·|AM|,
所以m2=λ[(x1-m)2+y eq \\al(\s\up1(2),\s\d1(1)) ],
因为y eq \\al(\s\up1(2),\s\d1(1)) =4x1,λx1=m,
所以m2= eq \f(m,x1) [(x1-m)2+4x1],
整理得:x eq \\al(\s\up1(2),\s\d1(1)) -(3m-4)x1+m2=0,③
因为过点M的直线与抛物线交于A,B两点,
所以关于x1的方程③有两正数根,
所以 eq \b\lc\{(\a\vs4\al\c1(3m-4>0,m2>0,Δ=(3m-4)2-4m2≥0)) ,解得m≥4.
抛物线的综合问题
角度1 抛物线与其他曲线的综合
[典例5](1)(2023·锦州模拟)已知抛物线C:y2=2px(p>0)的焦点为F,点P是C上一点,且|PF|=5,以PF为直径的圆截x轴所得的弦长为1,则p=( )
A.2 B.2或4
C.4 D.4或6
解析:选D.设圆的圆心为M,与x轴交于点F,B,线段FB的中点为A,MA⊥x轴,
由条件可知 eq \b\lc\|\rc\|(\a\vs4\al\c1(MF)) = eq \f(5,2) , eq \b\lc\|\rc\|(\a\vs4\al\c1(FA)) = eq \f(1,2) , eq \b\lc\|\rc\|(\a\vs4\al\c1(MA)) = eq \r(\f(25,4)-\f(1,4)) = eq \r(6) ,
所以yP=2 eq \r(6) ,由焦半径公式可知xP+ eq \f(p,2) =5,即xP=5- eq \f(p,2) ,
所以代入抛物线方程得24=2p(5- eq \f(p,2) ),
解得p=4或6.
(2)(2022·苏州模拟)若双曲线C1:y2-3x2=λ(λ≠0)的右焦点与抛物线C2:y2=8x的焦点重合,则实数λ=( )
A.±3 B.- eq \r(3) C.3 D.-3
解析:选D.双曲线C1的右焦点与抛物线的焦点(2,0)重合,所以双曲线C1的方程化为 eq \f(y2,λ) - eq \f(x2,\f(λ,3)) =1(λ≠0),
再转化为 eq \f(x2,-\f(λ,3)) - eq \f(y2,-λ) =1(λ<0),
所以a2=- eq \f(λ,3) ,b2=-λ,
所以c2=a2+b2=- eq \f(λ,3) -λ=- eq \f(4,3) λ,
所以c= eq \r(-\f(4,3)λ) ,
所以 eq \r(-\f(4,3)λ) =2,平方得λ=-3.
角度2 最小值问题
[典例6]抛物线y=4x2上一点到直线y=4x-5的距离最短,则该点的坐标是________.
解析:方法一:设与y=4x-5平行的直线y=4x+b与y=4x2相切,将y=4x+b代入y=4x2,得4x2-4x-b=0.①
由Δ=16+16b=0得b=-1,代入①得x= eq \f(1,2) ,
所以所求点的坐标为( eq \f(1,2) ,1).
方法二:设该点坐标为A(x0,y0),那么有y0=4x eq \\al(\s\up1(2),\s\d1(0)) .
设点A到直线y=4x-5的距离为d,
则d= eq \f(|4x0-y0-5|,\r(42+1)) = eq \f(1,\r(17)) |-4x eq \\al(\s\up1(2),\s\d1(0)) +4x0-5|
= eq \f(1,\r(17)) |4x eq \\al(\s\up1(2),\s\d1(0)) -4x0+5|= eq \f(1,\r(17)) |4(x0- eq \f(1,2) )2+4|.
当且仅当x0= eq \f(1,2) 时,d有最小值,
将x0= eq \f(1,2) 代入y=4x2解得y0=1.
故点A的坐标为( eq \f(1,2) ,1).
答案:( eq \f(1,2) ,1)
1.求解抛物线与其他圆锥曲线的综合问题时,要注意距离的转换,如将抛物线上的点到焦点的距离转换为抛物线上的点到准线的距离,这样可以简化运算过程.
2.与抛物线有关的最值问题的两个转化策略
(1)将抛物线上的点到准线的距离转化为该点到焦点的距离,利用“两点之间线段最短”来解决问题;
(2)将抛物线上的点到焦点的距离转化为该点到准线的距离,利用“与直线上所有点的连线中垂线段最短”来解决问题.
1.抛物线C:x2=2py(p>0)的焦点为F,其准线与双曲线 eq \f(x2,3) - eq \f(y2,3) =1相交于A,B两点,若△ABF为等边三角形,则p=( )
A.3 B.6 C.4 D.8
解析:选B.由题意得: eq \b\lc\|\rc\|(\a\vs4\al\c1(FD)) =p, eq \b\lc\|\rc\|(\a\vs4\al\c1(OD)) = eq \f(p,2) ,
因为△ABF为等边三角形,
所以 eq \b\lc\|\rc\|(\a\vs4\al\c1(BD)) = eq \f(\r(3),3) p,
所以B( eq \f(\r(3)p,3) ,- eq \f(p,2) ),将B( eq \f(\r(3)p,3) ,- eq \f(p,2) )代入方程 eq \f(x2,3) - eq \f(y2,3) =1得p=6.
2.若拋物线y2=8x的焦点也是双曲线 eq \f(x2,a2) -y2=1(a>0)的焦点,则a=________.
解析:因为拋物线y2=8x的焦点为F(2,0),
且该点也是双曲线 eq \f(x2,a2) -y2=1(a>0)的焦点,
所以a2+12=4,
又因为a>0,所以a= eq \r(3) .
答案: eq \r(3)
3.(2023·济南模拟)已知抛物线方程为y2=4x,直线l:x+y+ eq \r(2) =0,抛物线上一动点P到直线l的距离的最小值为________.
解析:设与直线l平行且与抛物线相切的直线方程为x+y+m=0,
由 eq \b\lc\{(\a\vs4\al\c1(x+y+m=0,y2=4x)) ,得y2+4y+4m=0,
则Δ=16-16m=0,得m=1,
所以切线方程为x+y+1=0,
所以抛物线上一动点P到直线l的距离的最小值为d= eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(\r(2)-1)),\r(2)) = eq \f(2-\r(2),2) .
答案: eq \f(2-\r(2),2)
【加练备选】
以抛物线C:y2=4x的焦点F为圆心的圆交C于A,B两点,交C的准线于D,E两点,已知 eq \b\lc\|\rc\|(\a\vs4\al\c1(AB)) =8,则 eq \b\lc\|\rc\|(\a\vs4\al\c1(DE)) =__________.
解析:由抛物线方程知: eq \f(p,2) =1,所以F(1,0),
不妨设点A在第一象限,如图所示,
由 eq \b\lc\|\rc\|(\a\vs4\al\c1(AB)) =8,y2=4x,得A(4,4),
所以圆的半径r= eq \r(32+42) =5,
所以 eq \b\lc\|\rc\|(\a\vs4\al\c1(DE)) =2 eq \r(r2-p2) =2 eq \r(25-4) =2 eq \r(21) .
答案:2 eq \r(21)
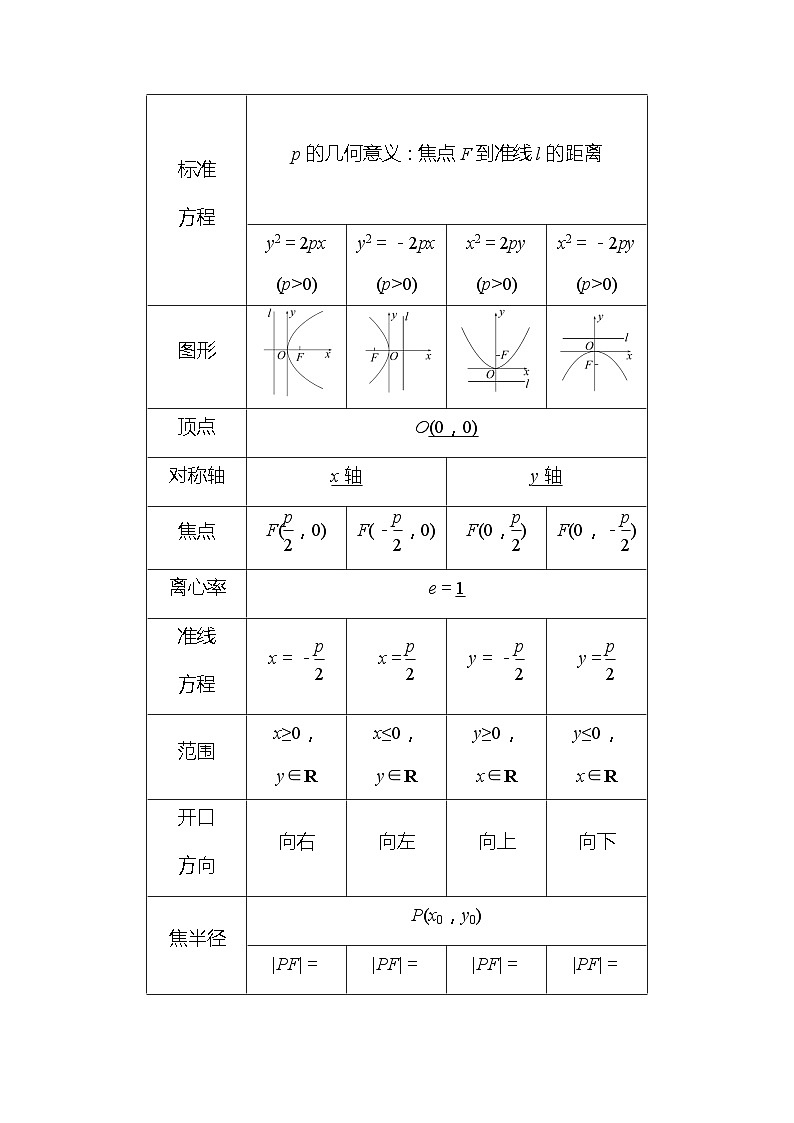
标准
方程
p的几何意义:焦点F到准线l的距离
y2=2px
(p>0)
y2=-2px
(p>0)
x2=2py
(p>0)
x2=-2py
(p>0)
图形
顶点
O(0,0)
对称轴
x轴
y轴
焦点
F( eq \f(p,2) ,0)
F(- eq \f(p,2) ,0)
F(0, eq \f(p,2) )
F(0,- eq \f(p,2) )
离心率
e=1
准线
方程
x=- eq \f(p,2)
x= eq \f(p,2)
y=- eq \f(p,2)
y= eq \f(p,2)
范围
x≥0,
y∈R
x≤0,
y∈R
y≥0,
x∈R
y≤0,
x∈R
开口
方向
向右
向左
向上
向下
焦半径
P(x0,y0)
|PF|=
x0+ eq \f(p,2)
|PF|=
-x0+ eq \f(p,2)
|PF|=
y0+ eq \f(p,2)
|PF|=
-y0+ eq \f(p,2)
教材改编
结论应用
易错易混
1,3
5
2,4
方法一
分情况讨论,注意要对四种形式的标准方程进行讨论,对于焦点在x轴上的抛物线,为避免开口方向不确定可分为y2=2px(p>0)和y2=-2px(p>0)两种情况求解.
方法二
设成y2=mx(m≠0),若m>0,开口向右;若m<0,开口向左;若m有两个解,则抛物线的标准方程有两个.同理,焦点在y轴上的抛物线可以设成x2=my(m≠0).
高考数学复习第九章 第二节 两条直线的位置关系(导学案): 这是一份高考数学复习第九章 第二节 两条直线的位置关系(导学案),共15页。学案主要包含了课程标准,必备知识 精归纳,常用结论,基础小题 固根基,方法提炼,对点训练,加练备选,一题多变等内容,欢迎下载使用。
高考数学复习拓展提升课十一 抛物线的结论及其应用(导学案): 这是一份高考数学复习拓展提升课十一 抛物线的结论及其应用(导学案),共6页。学案主要包含了常用结论,结论证明等内容,欢迎下载使用。
2023届高考一轮复习讲义(理科)第九章 平面解析几何 第7讲 抛物线学案: 这是一份2023届高考一轮复习讲义(理科)第九章 平面解析几何 第7讲 抛物线学案,共23页。学案主要包含了知识梳理,习题改编等内容,欢迎下载使用。