2024年四川成都青羊区四川省成都市石室中学高三下学期高考模拟理科数学试卷（高考适应性（二））

这是一份2024年四川成都青羊区四川省成都市石室中学高三下学期高考模拟理科数学试卷（高考适应性（二）），共6页。试卷主要包含了单选题，星期六，填空题，解答题等内容，欢迎下载使用。

2024年四川成都青羊区四川省成都市石室中学高三下学期高考模拟理科数学试
卷（高考适应性（二））
一、单选题
1.若集合
A.
，
，则
（
）
B. [0，1]
C.
D.
2.已知复数
值为（
A. 2
（
， 为虚数单位），其在复平面内对应向量的模为2，则
的最大
）
B. 3
C.
D.
3.甲乙两名同学6次考试的成绩统计如图，甲乙成绩的平均数分别为
（
，
，标准差分别为
，
，则
）
A.
，
B.
，
C.
，
D.
，
4.若 ， 为不垂直的异面直线， 是一个平面，刚 ， 在 上的射影有可能是：
①两条平行直线；②两条互相垂直的直线；③同一条直线；④一条直线及直线外一点
其中，正确结论的序号是（
A. ①②③
）
B. ②③④
C. ①③④
D. ①②④
，则(
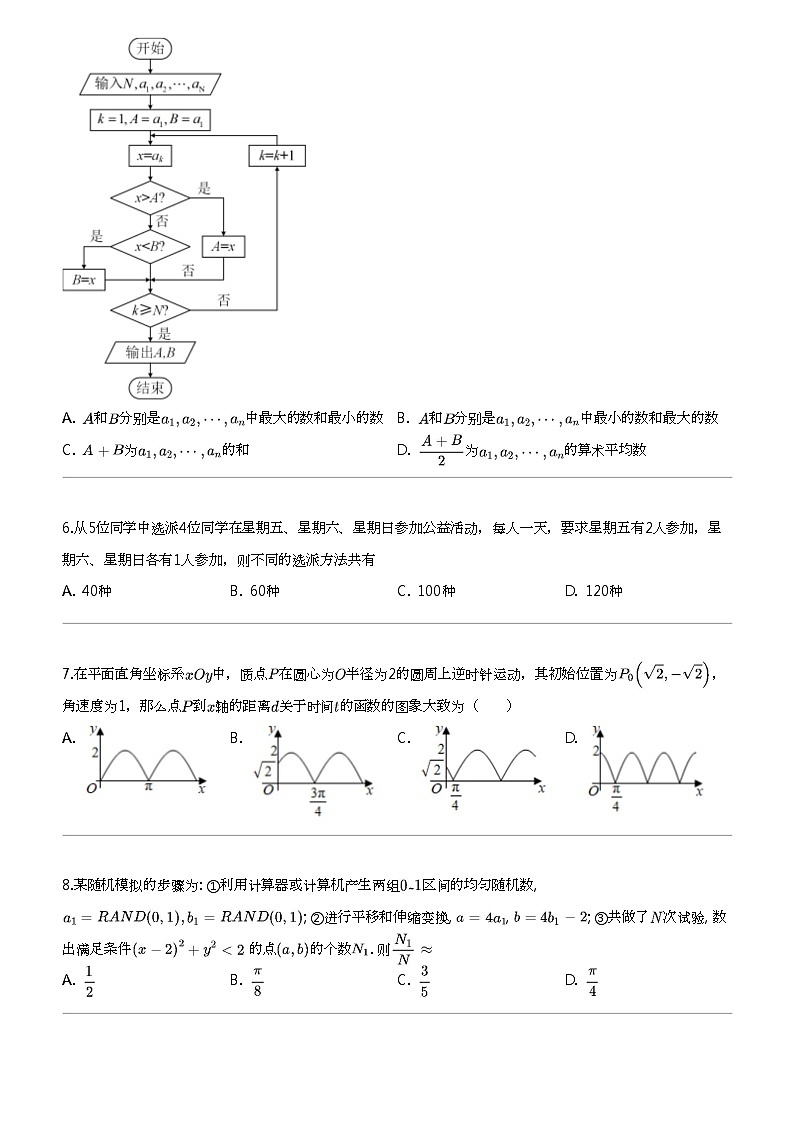
5.如果执行下边的程序框图，输入正整数
和实数
，输出
)

A. 和 分别是
C.
中最大的数和最小的数 B. 和 分别是
的和 D.
中最小的数和最大的数
的算术平均数
为
为
6.从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有2人参加，星
期六、星期日各有1人参加，则不同的选派方法共有
A. 40种
B. 60种
C. 100种
D. 120种
7.在平面直角坐标系
中，质点 在圆心为 半径为2的圆周上逆时针运动，其初始位置为
，
角速度为1，那么点 到 轴的距离 关于时间 的函数的图象大致为（
A. B. C.
）
D.
8.某随机模拟的步骤为: ①利用计算器或计算机产生两组
区间的均匀随机数,
; ②进行平移和伸缩变换,
的个数 . 则
,
; ③共做了 次试验, 数
出满足条件
A.
的点
B.
C.
D.

9.一边长为4的正方形ABCD，M为AB的中点，将
，
分别沿MD，MC折起，使MA，MB重
D.
合，得到一个四面体，则该四面体外接球的表面积为（
）．
A.
B.
C.
10.已知
A. 1
，则
的值为（
）
B.
C. 2
D.
11.已知圆
在椭圆
的内部，点 为 上一动点.
过 作圆 的一条切线，交 于另一点 ，切点为 ，当 为
的中点时，直线
的斜率为
，则 的
离心率为（
A.
）
B.
C.
D.
12.已知函数
的定义域为 ，且
B.
，若
，则下列结论错误的是
（
A.
）
C. 函数
函数
是偶 D. 函数
函数
是减
二、填空题
13.已知向量
满足
，且 是单位向量，若
，则
．
14.关于双曲线
，四位同学给出了四个说法：
小明：双曲线 的实轴长为8；
小红：双曲线 的焦点到渐近线的距离为3；
小强：双曲线 的离心率为 ；
小同：双曲线C上的点到焦点距离的最小值为1；
若这4位同学中只有1位同学的说法错误，则说法错误的是
强”或“小同”）
．（横线上填“小明”、“小红”、“小

15.已知函数
的图象与函数
（
且
）的图象在公共点处有相同的切线，则公共点坐标
为
.
16.定义在封闭的平面区域D内任意两点的距离的最大值称为平面区域D的“直径”．如图，已知锐角三角形的
三个顶点A，B，C在半径为1的圆上，角的对边分别为a，b，c，
．分别以
各边为直径向外作三
．
个半圆，这三个半圆和
构成平面区域D，则平面区域D的“直径”的取值范围是
三、解答题
17.已知数列
(1)求数列
(2)设
的前 项和为
的通项公式
，
，
．
，记数列
的前 项和为 ，证明
．
18.如图，在三棱锥
中，
．
， 为
的中点，
于 ，
，已知
，
，
，
(1)证明：
平面
；
(2)在线段
上是否存在点 ，使得二面角
的大小为 ？若存在，求出
的长；若不存在，
请说明理由．

19.某机构为了解2023年当地居民网购消费情况，随机抽取了100人，对其2023年全年网购消费金额（单位：
千元）进行了统计，所统计的金额均在区间 ， 内，并按 ， ， ，
所示的频率分布直方图．
，
，
分成6组，制成如图
(1)求图中 的值；
(2)若将全年网购消费金额在20千元及以上者称为网购迷，结合图表数据，补全
的把握认为样本数据中网购迷与性别有关系？说明理由．
列联表，并判断是否有
合计
男
女
网购迷
非网购迷
合计
20
47
(3)若甲、乙两位网购迷网购时支付方式采用软件 支付分概率分别为
，采用其它支付方式的概率分别为
，且甲、乙两人网购时采用支付方式相互独立．在甲、乙各自独立完成的2次网购中，记甲、乙两人支付
方式采用 支付的次数分别为 ， ，令
下面的临界值表仅供参考：
，求 的分布列和数学期望
0.15
0.10
2.706
0.05
0.025
5.024
0.010
6.635
0.005
7.879
0.001
2.072
3.841
10.828
（参考公式：
，其中
20.已知函数
(1)当
．
的单调区间；
时，求
时，
(2)当
，求 的取值范围．
21.已知直线
过定点 ，动圆 过点 ，且在 轴上截得的弦长为4，设动圆圆心轨迹为曲线 .
(1)求曲线 的方程；

(2)点
， ， 为 上的两个动点，若 ， ， 恰好为平行四边形
的其中三个顶点，且该平行四
.
边形对角线的交点在
上，记平行四边形
的面积为 ，求证：
22.在直角坐标系
（t为参数）．
中，曲线 的参数方程为
（ 为参数），曲线 的参数方程为
(1)写出
及
的普通方程；
(2)以坐标原点 为极点， 轴正半轴为极轴建立极坐标系，求
与
交点的极坐标．
23.已知函数
．
(1)求
(2)若
的最小值；
的最小值为 ，正实数a，b，c满足
，求证: