2024年广东省广州市番禺区中考数学二模试卷（含解析）

这是一份2024年广东省广州市番禺区中考数学二模试卷（含解析），共20页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

1.6的相反数是( )
A. 6B. −6C. 16D. −16
2.如图所示的圆锥，下列说法正确的是( )
A. 该圆锥的主视图是轴对称图形
B. 该圆锥的主视图是中心对称图形
C. 该圆锥的主视图既是轴对称图形，又是中心对称图形
D. 该圆锥的主视图既不是轴对称图形，又不是中心对称图形
3.二次根式 x−1有意义的条件是( )
A. x≥1B. x>1C. x≥0D. x>0
4.下列运算正确的是( )
A. a+ b= a+bB. (x2)5=x10
C. x5⋅x6=x30D. 2 a×3 a=6 a
5.为了庆祝中国共产党成立100周年，某校举办了党史知识竞赛活动，在获得一等奖的学生中，有3名女学生，1名男学生，则从这4名学生中随机抽取2名学生，恰好抽到2名女学生的概率为( )
A. 23B. 12C. 13D. 16
6.若点A(−1,y1)，B(2,y2)，C(3,y3)在反比例函数y=6x的图象上，则y1，y2，y3的大小关系是( )
A. y37.如图，AB，AC是⊙O的弦，OB，OC是⊙O的半径，点P为OB上任意一点(点P不与点B重合)，连接CP.若∠BAC=70°，则∠BPC的度数可能是( )
A. 70°
B. 105°
C. 125°
D. 155°
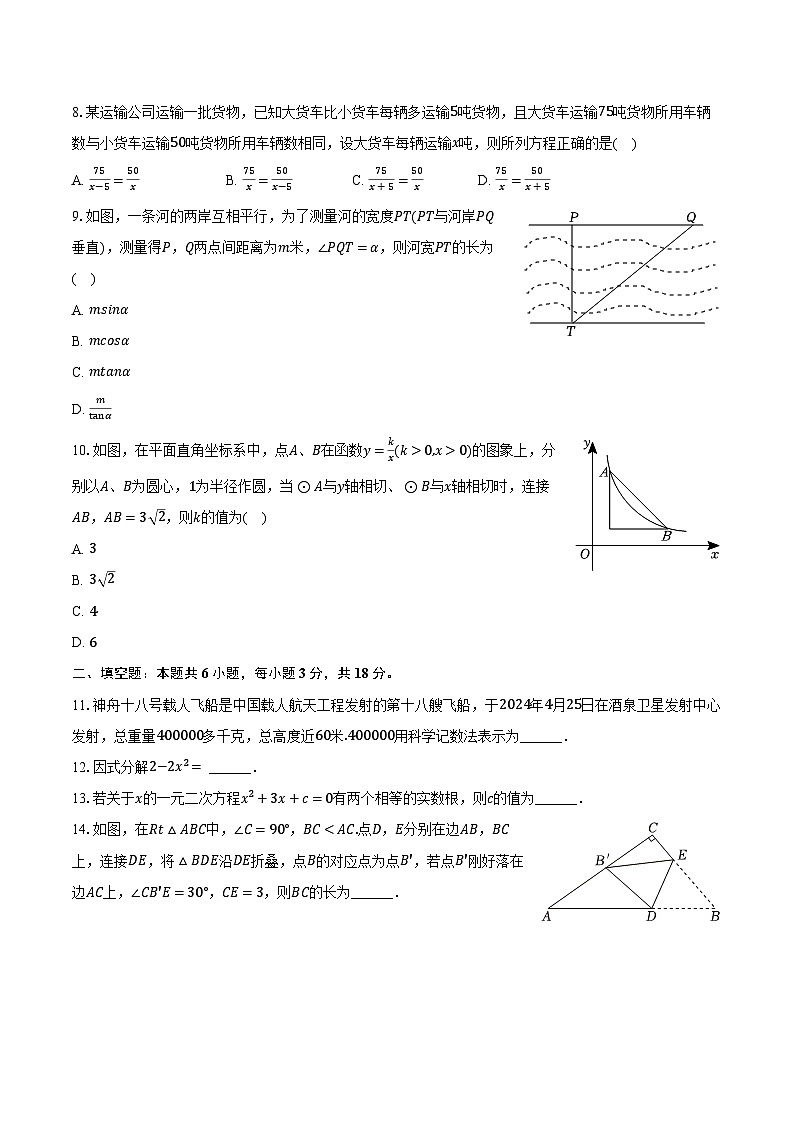
8.某运输公司运输一批货物，已知大货车比小货车每辆多运输5吨货物，且大货车运输75吨货物所用车辆数与小货车运输50吨货物所用车辆数相同，设大货车每辆运输x吨，则所列方程正确的是( )
A. 75x−5=50xB. 75x=50x−5C. 75x+5=50xD. 75x=50x+5
9.如图，一条河的两岸互相平行，为了测量河的宽度PT(PT与河岸PQ垂直)，测量得P，Q两点间距离为m米，∠PQT=α，则河宽PT的长为( )
A. msinα
B. mcsα
C. mtanα
D. mtanα
10.如图，在平面直角坐标系中，点A、B在函数y=kx(k>0,x>0)的图象上，分别以A、B为圆心，1为半径作圆，当⊙A与y轴相切、⊙B与x轴相切时，连接AB，AB=3 2，则k的值为( )
A. 3
B. 3 2
C. 4
D. 6
二、填空题：本题共6小题，每小题3分，共18分。
11.神舟十八号载人飞船是中国载人航天工程发射的第十八艘飞船，于2024年4月25日在酒泉卫星发射中心发射，总重量400000多千克，总高度近60米.400000用科学记数法表示为______．
12.因式分解2−2x2= ______．
13.若关于x的一元二次方程x2+3x+c=0有两个相等的实数根，则c的值为______．
14.如图，在Rt△ABC中，∠C=90°，BC15.如图，正方形ABCD边长为3，点E在边AB上，以E为旋转中心，将EC逆时针旋转90°得到EF，AD与FE交于P点，若tan∠BCE=13，则PF的值为______．
16.如图1，点P从△ABC的顶点A出发，沿着A→B→C的方向运动，到达点C后停止.设P点的运动时间为x，AP的长度为y，图2是y与x的关系图象，其中E点是曲线部分的最低点，则△ABC的面积是______．
三、计算题：本大题共1小题，共4分。
17.解方程组：x−y=1x+3y=9．
四、解答题：本题共8小题，共68分。解答应写出文字说明，证明过程或演算步骤。
18.(本小题4分)
已知：如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C.求证：∠A=∠D．
19.(本小题6分)
已知A=(mn−nm)⋅ 3mnm−n．
(1)化简A；
(2)若m+n−2 3=0，求A的值．
20.(本小题6分)
某初中学校为加强劳动教育，开设了劳动技能培训课程.为了解培训效果，学校对七年级320名学生在培训前和培训后各进行一次劳动技能检测，两次检测项目相同，评委依据同一标准进行现场评估，分成“合格”、“良好”、“优秀”3个等级，依次记为2分、6分、8分(比如，某同学检测等级为“优秀”，即得8分).学校随机抽取32名学生的2次检测等级作为样本，绘制成下面的条形统计图：
(1)这32名学生在培训前得分的中位数对应等级应为______；(填“合格”、“良好”或“优秀”)
(2)求这32名学生培训后比培训前的平均分提高了多少？
(3)利用样本估计该校七年级学生中，培训后检测等级为“良好”与“优秀”的学生人数之和是多少？
21.(本小题8分)
2023年5月30日9点31分，“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射，成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站.如图，在发射的过程中，飞船从地面O处发射，当飞船到达A点时，从位于地面C处的雷达站测得AC的距离是8km，仰角为30°；10s后飞船到达B处，此时测得仰角为45°．
(1)求点A离地面的高度AO；
(2)求飞船从A处到B处的平均速度.(结果精确到0.1km/s，参考数据： 3≈1.73)
22.(本小题10分)
设函数y1=k1x，函数y2=k2x+b(k1,k2,b是常数，k1≠0，k2≠0)．
(1)若函数y1和函数y2的图象交于点A(1,m)，点B(3,1)，
①求函数y1，y2的表达式；
②当2(2)若点C(2,n)在函数y1的图象上，点C先向下平移2个单位，再向左平移4个单位，得点D，点D恰好落在函数y1的图象上，求n的值．
23.(本小题10分)
如图，在▱ABCD中，AB=5，AD=3 2，∠A=45°．
(1)尺规作图：将▱ABCD沿着经过A点的某条直线翻折，使点B落在CD边上的点E处，请作出折痕，折痕与BC的交点为F.(不写作法，保留作图痕迹)
(2)若折痕AF与DC的延长线交于点G．
①求EG的长度；
②求点G到直线AE的距离．
24.(本小题12分)
如图，AB为⊙O的直径，OA=3，点M在直线AB的下方且将AB平分，动点P在⊙O上且位于直线AB上方，连接OP，作点A关于直线OP的对称点A′，连接OA′．

(1)当A′与点B重合时，则∠AOP= ______；
(2)当PA′⊥AB时，求AA′的长度；
(3)△A′BM能否等腰三角形？如果能，求出此时AA′的长度；如果不能，请说明理由．
25.(本小题12分)
已知抛物线y=x2−(m+1)x+m(m<0)．
(1)当m=0时，求抛物线与x轴的交点坐标；
(2)若抛物线与x轴有两个不同的交点A、B(点A在点B的左侧)，与y轴交于点C，过点C作直线l//x轴，点E是直线l上的一动点，点F是y轴上的一动点，且EF=2 2．
①当点E落在抛物线上(不与点C重合)，且AE=EF时，求m的值；
②取EF的中点M，是否存在AM的最小值为 22？若存在，求出此时m的值，若不存在，请说明理由．
答案和解析
1.【答案】B
【解析】【分析】
此题主要考查了相反数的含义以及求法，要熟练掌握，解答此题的关键是要明确：相反数是成对出现的，不能单独存在．
求一个数的相反数的方法就是在这个数的前边添加一个“−”，据此解答即可．
【解答】
解：根据相反数的含义，可得
6的相反数是：−6．
故选：B．
2.【答案】A
【解析】【分析】
本题主要考查简单几何体的三视图，解题的关键是掌握常见几何体的三视图及轴对称图形、中心对称图形的概念．
【解答】
圆锥的主视图是等腰三角形，是轴对称图形，但不是中心对称图形，
故选：A。
3.【答案】A
【解析】解：∵二次根式 x−1有意义，
∴x−1≥0，即x≥1．
故选A．
根据二次根式有意义的条件得到x−1≥0，然后解不等式即可．
本题考查了二次根式有意义的条件： a有意义的条件为a≥0．
4.【答案】B
【解析】解：A、 a与 b不是同类二次根式，故不能合并，故A不符合题意．
B、原式=x10，故B符合题意．
C、原式=x11，故C不符合题意．
D、原式=6a，故D不符合题意．
故选：B．
根据二次根式的加减与乘法运算、幂的乘方运算、同底数幂的乘法运算即可求出答案．
本题考查二次根式的加减与乘法运算、幂的乘方运算、同底数幂的乘法运算，本题属于基础题型．
5.【答案】B
【解析】【分析】
此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
画树状图，共有12种等可能的结果，恰好抽到2名女学生的结果有6种，再由概率公式求解即可．
【解答】
解：画树状图如图：
共有12种等可能的结果，恰好抽到2名女学生的结果有6种，
∴恰好抽到2名女学生的概率为612=12，
故选：B．
6.【答案】C
【解析】解：∵点A(−1,y1)，B(2,y2)，C(3,y3)在反比例函数y=6x的图象上，
∴y1=6−1=−6，y2=62=3，y3=63=2，
又∵−6<2<3，
∴y1故选：C．
根据反比例函数图象上点的坐标特征求出y1、y2、y3的值，比较后即可得出结论．
本题考查了反比例函数图象上点的坐标特征，利用反比例函数图象上点的坐标特征求出y1、y2、y3的值是解题的关键．
7.【答案】D
【解析】解：如图，连接BC，
∵∠BAC=70°，
∴∠BOC=2∠BAC=140°，
∵OB=OC，
∴∠OBC=∠OCB=180°−140°2=20°，
∵点P为OB上任意一点(点P不与点B重合)，
∴0°<∠OCP<20°，
∵∠BPC=∠BOC+∠OCP=140°+∠OCP，
∴140°<∠BPC<160°，
故选：D．
利用圆周角定理求得∠BOC的度数，然后利用三角形外角性质及等边对等角求得∠BPC的范围，继而得出答案．
本题考查圆与三角形外角性质的综合应用，结合已知条件求得∠BPC的范围是解题的关键．
8.【答案】B
【解析】解：∵每辆大货车的货运量是x吨，
∴每辆小货车的货运量是( x−5)吨，
依题意得：75x=50x−5．
故选：B．
由每辆大货车的货运量是x吨，则每辆小货车的货运量是(x−5)吨，根据用大货车运送75吨货物所需车辆数与小货车运送50吨货物所需车辆数相同，即可得出关于x的分式方程．
本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．
9.【答案】C
【解析】解：由题意得：
PT⊥PQ，
∴∠APQ=90°，
在Rt△APQ中，PQ=m米，∠PQT=α，
∴PT=PQ⋅tanα=mtanα(米)，
∴河宽PT的长度是mtanα米，
故选：C．
根据垂直定义可得PT⊥PQ，然后在Rt△PQT中，利用锐角三角函数的定义进行计算即可解答．
本题考查了解直角三角形的应用，熟练掌握锐角三角函数的定义是解题的关键．
10.【答案】C
【解析】解：由题意，得A(1,k)，B(k,1)．
∵AB=3 2，
∴有两点距离公式可得：2(k−1)2=18．
∴(k−1)2=9．
∴k=−2或4．
又k>0，
∴k=4．
故选：C．
依据题意，可得A(1,k)，B(k,1)，再由AB=3 2，从而2(k−1)2=18，进而得解．
本题考查了反比例函数的图象与性质的应用，解题时需要熟练掌握并理解．
11.【答案】4×105
【解析】解：400000=4.09×105，
故答案为：4×105．
将一个数表示成a×10n的形式，其中1≤|a|<10，n为整数，这种记数方法叫做科学记数法，据此即可求得答案．
本题考查科学记数法，熟练掌握其定义是解题的关键．
12.【答案】2(1+x)(1−x)
【解析】解：2−2x2
=2(1−x2)
=2(1+x)(1−x)，
故答案为：2(1+x)(1−x)．
先提公因式，再利用平方差公式继续分解即可解答．
本题考查了提公因式法与公式法的综合运用，一定要注意如果多项式的各项含有公因式，必须先提公因式．
13.【答案】94
【解析】解：∵关于x的一元二次方程x2+2x−c=0有两个相等的实数根，
∴Δ=32−4c=0，
解得c=94，
故答案为：94．
根据判别式的意义得到Δ=32+4c=0，解得即可．
本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2−4ac：当Δ>0，方程有两个不相等的实数根；当Δ=0，方程有两个相等的实数根；当Δ<0，方程没有实数根．
14.【答案】9
【解析】解：∵将△BDE沿DE折叠，点B的对应点为点B′，若点B′刚好落在边AC上，
在Rt△ABC中，∠C=90°，BC∴B′E=BE=2CE=6，
∴BC=CE+BE=3+6=9．
故答案为：9．
根据折叠的性质以及含30°角的直角三角形的性质得出B′E=BE，=2CE=6即可求解．
本题考查了折叠的性质，含30°角的直角三角形的性质熟练掌握以上性质是解题关键．
15.【答案】 103
【解析】解：∵tan∠BCE=13=BEBC，BC=3，
∴BE=1，
∴AE=2，CE= BC2+BE2= 1+9= 10，
∵将EC逆时针旋转90°得到EF，
∴EF=CE= 10，∠FEC=90°，
∴∠CEB+∠AEP=90°=∠CEB+∠BCE，
∴∠AEP=∠BCE，
又∵∠A=∠B=90°，
∴△AEP∽△BCE，
∴AEBC=PEEC，
∴23=PE 10，
∴PE=2 103，
∴PF= 103，
故答案为： 103．
由锐角三角函数可求BE=1，通过证明△AEP∽△BCE，可求PE的长，即可求解．
本题考查了旋转的性质，正方形的性质，锐角三角函数，相似三角形的判定和性质，证明三角形相似是解题的关键．
16.【答案】9 32+6
【解析】解：作AH⊥BC，如图，
当点P到点B处时，y=5，即AB=5，
当点P到点H处时AP最短，y=3，即AH=3，
当点P到点C处时，y=6，即AC=6，
在Rt△ABH中，BH= 52−32=4，
在Rt△ACH中，CH= 62−32=3 3，
∴S△ABC=12BC⋅AH=9 32+6．
分析出当点P到点B处时，y=5，即AB=5，当点P到点H处时AP最短，y=3，即AH=3，当点P到点C处时，y=6，即AC=6，再根据勾股定理分别求出BH和CH，即可求出三角形的面积．
本题考查了动点问题的函数图象，准确的分析动点的运动位置，获得相应的解题条件是本题的解题关键．
17.【答案】解：x−y=1 ①x+3y=9 ②，
②−①得，4y=8，解得y=2，
把y=2代入①得，x−2=1，解得x=3，
故原方程组的解为x=3y=2．
【解析】运用加减消元解答即可．
此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
18.【答案】证明：∵BE=CF，
∴BE+EF=CF+EF，
∴BF=CE，
在△ABF和△DCE中，
AB=CD∠B=∠CBF=CE，
∴△ABF≌△DCE(SAS)，
∴∠A=∠D．
【解析】根据SAS证明△ABF≌△DCE，由全等三角形的性质即可解决问题．
本题考查全等三角形的判定和性质，解题的关键是正确寻找全等三角形全等的条件，属于中考基础题．
19.【答案】解：(1)A=(mn−nm)⋅ 3mnm−n
=m2−n2mn⋅ 3mnm−n
=(m+n)(m−n)mn⋅ 3mnm−n
= 3(m+n)；
(2)∵m+n−2 3=0，
∴m+n=2 3，
当m+n=2 3时，
A= 3×2 3=6．
【解析】本题主要考查了分式的化简求值，熟练运用分式运算法则化简是解题的关键，注意代入计算要仔细，属于常考题型．
(1)根据分式的减法和乘法可以化简A；
(2)根据m+n−2 3=0，可以得到m+n=2 3，然后代入(1)中化简后的A，即可求得A的值．
20.【答案】解：(1)合格；
(2)培训前的平均分为：(25×2+5×6+2×8)÷32=3(分)，
培调后的平均分为：(8×2+16×6+8×8)÷32=5.5(分)，
5.5−3=2.5(分)，
培训后比培训前的平均分提高了2.5分；
(3)培训后考分等级为“合格”与“优秀”的学生共有320×16+832=240(名)，
答：培训后检测等级为“良好”与“优秀”的学生人数之和是240名．
【解析】解：(1)由题意得，这32名学生在培训前得分的中位数对应等级应为合格，
故答案为：合格；
(2)(3)见答案．
(1)中位数是将一组数据从小到大(或从大到小)重新排列后，最中间的那个数(最中间两个数的平均数)；
(2)根据加权平均数的计算公式计算即可；
(3)用样本估计总体即可．
本题考查的是条形统计图、中位数、加权平均数的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．
21.【答案】解：(1)在Rt△AOC中，∵∠AOC=90°，∠ACO=30°，AC=8km，
∴AO=12AC=12×8=4(km)，
(2)在Rt△AOC中，∵∠AOC=90°，∠ACO=30°，AC=8km，
∴OC= 32AC=4 3(km)，
在Rt△BOC中，∵∠BOC=90°，∠BCO=45°，
∴∠BCO=∠OBC=45°，
∴OB=OC=4 3km，
∴AB=OB−OA=(4 3−4)km，
∴飞船从A处到B处的平均速度=4 3−410≈0.3(km/s)．
【解析】(1)根据直角三角形的性质即可得到结论；
(2)在Rt△AOC中，根据直角三角形的性质得到OC= 32AC=4 3(km)，在Rt△BOC中，根据等腰直角三角形的性质得到OB=OC=4 3km，于是得到结论．
本题考查了解直角三角形−仰角俯角问题，正确地求得结果是解题的关键．
22.【答案】解：(1)把点B(3,1)代入y1=k1x，
3=k11，
解得：k1=3，
∴函数y1的表达式为y1=3x，
把点A(1,m)代入y1=3x，解得m=3，
把点A(1,3)，点B(3,1)代入y2=k2x+b，
3=k2+b1=3k2+b，
解得k2=−1b=4，
∴函数y2的表达式为y2=−x+4；
(2)如图，

当2(3)由平移，可得点D坐标为(−2,n−2)，
∴−2(n−2)=2n，
解得：n=1，
∴n的值为1．
【解析】(1)①利用待定系数法求函数解析式；
②利用函数图像分析比较；
(2)根据平移确定点D的坐标，然后利用函数图像上点的坐标特征代入求解．
本题考查反比例函数与一次函数，理解反比例函数和一次函数的图像性质，掌握待定系数法求函数解析式，利用数形结合思想解题是关键．
23.【答案】解：(1)如图所示；
(2)①由作图得：AG平分∠BAE，AE=AB=5，
∴∠EAG=∠GAB，
在▱ABCD中，有CD/​/AB，
∴∠EAG=∠GAB，
∴∠EAG=∠EGA，
∴EG=AE=5；
②过D作DH⊥AB于H，
则：DH=ADsin∠BAD=3，
∵AG平分∠BAE，
∴点G到直线AE的距离等于G到AB的距离，也等于DH=3，
∴点G到直线AE的距离为3．
【解析】(1)先作AE=AB，再根据等腰三角形的性质作图；
(2)①根据平行四边形的性质及等腰三角形的性质求解；
②根据角平分线的性质及三角函数求解．
本题考查了轴对称，掌握轴对称的性质、平行四边形的性质、三角函数的定义是解题的关键．
24.【答案】90°
【解析】解：(1)如图1，连接AA′，
∵点A′与点A关于直线OP对称，
∴OP垂直平分AA′，
∵AB为⊙O的直径，OA=3，
∴OA′=OA=3，
∴点A′在⊙O上，∠AOP=∠A′OP=12∠AOA′，
当A′与点B重合时，∠AOA′=∠AOB=180°，
∴∠AOP=12×180°=90°，
故答案为：90°．
(2)如图2，PA′⊥AB，则AA′=AP，
∴∠AOA′=∠AOP=∠A′OP=13×360°=120°，
∴∠A′OB=180°−∠AOA′=60°，
连接A′B，则∠AA′B=90°，
∵OA′=OB，
∴△A′OB是等边三角形，
∴A′B=OB=OA=3，
∴AB=6，
∴AA′= AB2−A′B2= 62−32=3 3，
∴AA′的长为3 3．
(3)能，
∵点M在直线AB的下方且将AB平分，
∴AM=BM，
∴∠AOM=∠BOM=12×180°=90°，
如图3，△A′BM是等腰三角形，且A′M=A′B，点A′在AB的上方，则∠A′OB=∠A′OM=12×(360−90°)=135°，
∴∠OA′B=∠OBA′=12×(180°−135°)=22.5°，
在A′B上截取A′C=AA′，连接AC，
∵∠AA′B=90°，
∴∠A′CA=∠A′AC=45°，
∴∠CAB=∠A′CA−∠OBA′=45°−22.5°=22.5°=∠OBA′，
∴BC=AC= AA′2+A′C2= 2AA′，
∴A′B= 2AA′+AA′，
∴AA′2+( 2AA′+AA′)2=62，
解得AA′=3 2− 2或−3 2− 2(不符合题意，舍去)；
如图4，△A′BM是等腰三角形，且A′B=MB，则∠A′OB=∠BOM=90°，
∴∠A′OB+∠BOM=180°，
∴A′、O、M三点在同一条直线上，
∴A′M垂直平分AB，
∴∠AOA′=90°，
∴AA′= OA2+OA′2= 2OA= 2×3=3 2；
如图5，△A′BM是等腰三角形，且A′M=A′B，点A′在AB的下方，则∠A′OB=∠A′OM=12×90°=45°，
作A′D⊥OB于点D，则∠A′DO=∠A′DB=90°，
∵A′DOD=tan45°=1，A′DOA′=sin45°= 22，
∴A′D=OD= 22OA′= 22×3=3 22，
∴AD=OA+OD=3+3 22，
∴AA′= AD2+A′D2= (3+3 22)2+(3 22)2=3 2+ 2，
综上所述，AA′的长是3 2− 2或3 2或3 2+ 2．
(1)连接AA′，则OP垂直平分AA′，因为AB为⊙O的直径，OA=3，所以OA′=OA=3，∠AOP=∠A′OP，当A′与点B重合时，∠AOA′=∠AOB=180°，则∠AOP=90°，于是得到问题的答案；
(2)当PA′⊥AB时，则AA′=AP，所以∠AOA′=∠AOP=∠A′OP=120°，则∠A′OB=60°，连接A′B，则∠AA′B=90°，可证明△A′OB是等边三角形，所以A′B=OB=OA=3，AB=6，求得AA′= AB2−A′B2=3 3；
(3)先证明∠AOM=∠BOM=90°，再分三种情况讨论，一是A′M=A′B，点A′在AB的上方，则∠A′OB=∠A′OM=135°，所以∠OA′B=∠OBA′=22.5°，在A′B上截取A′C=AA′，连接AC，可证明∠CAB=∠OBA′，则BC=AC= 2AA′，于是得AA′2+( 2AA′+AA′)2=62，求得AA′=3 2− 2；二是A′B=MB，则∠A′OB=∠BOM=90°，此时A′、O、M三点在同一条直线上，AA′= 2OA=3 2；三是A′M=A′B，点A′在AB的下方，则∠A′OB=∠A′OM=12×90°=45°，作A′D⊥OB于点D，则A′D=OD= 22OA′=3 22，求得AA′= AD2+A′D2=3 2+ 2．
此题重点考查轴对称的性质、垂径定理、直径所对的圆周角是直角、勾股定理、锐角三角函数与解直角三角形、数形结合与分类讨论数学思想的运用等知识与方法，此题综合性强，难度较大，属于考试压轴题．
25.【答案】解：(1)当m=0时，则y=x2−x，
当y=0时，即x2−x=0，
解得x1=0，x2=1；
∴抛物线与x轴的交点坐标为(0,0)，(1,0)；
(2)①∵抛物线y=x2−(m+1)x+m与x轴有两个不同的交点A、B(点A在点B的左侧)，与y轴交于点C，
∴0=x2−(m+1)x+m，
解得，x1=m，x2=1，
∵m<0，点A在点B的左侧，
∴A(m,0)，B(1,0)，点C(0,m)，点E(m+1,m)，
过点B作BH⊥l于点H，由点B(1,0)，得点H(1,m)．

在Rt△EBH中，EH=1−(m+1)=−m，HB=0−m=−m，
∴BE= EH2+HB2=− 2m，
∵AE=EF=2 2，
∴− 2m=2 2，
解得m=−2；
②存在，
理由：由M是EF的中点，连接CM，CA，得CM=12EF= 2，
根据题意，点M在以点C为圆心、 2为半径的圆上，
由点A(m,0)，点C(0,m)，得AO=−m，CO=−m，
∴在Rt△ACO中，AC= AO2+CO2=− 2m.
当AC≥ 2，即m≤−1时，满足条件的点M在线段AC上．
AM的最小值为AC−MC=− 2m− 2= 22，解得m=−32；
当AC< 2，即−1解得m=−12．
∴当m的值为−32或−12时，MN的最小值是 22．
【解析】(1)解方程即可得到结论；
(2)①根据题意得到0=x2−(m+1)x+m，解得x1=m，x2=1，求得A(m,0)，B(1,0)，点C(0,m)，点E(m+1,m)，过点B作BH⊥l于点H，由点B(1,0)，得点H(1,m).在Rt△EBH中，EH=1−(m+1)=−m，HB=0−m=−m，根据勾股定理得到BE= EH2+HB2=− 2m，解方程得到m=−2；
②由M是EF的中点，连接CM，CA，得CM=12EF= 2，根据题意得到点M在以点C为圆心、 2为半径的圆上，根据勾股定理得到AC= AO2+CO2=− 2m.当AC≥ 2，即m≤−1时，满足条件的点M在线段AC上．AM的最小值为AC−MC=− 2m− 2= 22，解得m=−32；当AC< 2，即−1本题是二次函数综合题，考查了二次函数的性质，待定系数法，二次函数图象上点的坐标特征，勾股定理等知识，熟练掌握二次函数的性质是解题的关键．