

山西省部分学校2023-2024学年高二下学期5月质量检测数学试题
展开考生注意:
1.本试卷分选择题和非选择题两部分。满分150分,考试时间120分钟。
2.答题前,考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。
3.考生作答时,请将答案答在答题卡上。选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,超出答题区域书写的答案无效,在试题卷、草稿纸上作答无效。
4.本卷命题范围:人教A版选择性必修第一册,选择性必修第二册,选择性必修第三册。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在一项中学生近视情况的调查中,某校150名男生中有80名近视,140名女生中有70名近视,在检验这些中学生近视是否与性别有关时最有说服力的方法是用( )
A.平均数与方差B.回归分析C.独立性检验D.概率
2.根据3对数据,,绘制的散点图知,样本点呈直线趋势,且线性回归方程为,则( )
A.11B.10C.9D.8
3.已知为等差数列,,,则( )
A.7B.5C.3D.1
4.在建立两个变量的回归模型中,分别选择4个不同模型,求出它们相对应的决定系数如下表,则其中拟合效果最好的模型是( )
A.模型1B.模型2C.模型3D.模型4
5.在的展开式中,x的系数为( )
A.B.C.D.
6.甲、乙两个箱子里各装有6个大小形状都相同的球,其中甲箱中有4个红球和2个白球,乙箱中有3个红球和3个白球.先从甲箱中随机取出1个球放入乙箱中,再从乙箱中随机取出1个球,则从乙箱中取出的球是红球的概率为( )
A.B.C.D.
7.在学校的书画展板上,将3幅书法作品,3幅美术作品按一圆形排列,要求美术作品不相邻,则不同排列方法有( )
A.36种B.24种C.18种D.12种
8.设,是双曲线的左、右焦点,点A是C的右支上一点,若的内切圆M的半径为a(M为圆心),且,使得,则双曲线C的离心率为( )
A.B.C.2D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。
9.对四组样本数据进行统计,获得如图所示的散点图,关于其样本相关系数的关系,正确的有( )
A.B.C.D.
10.某水果店经过统计30天的销售情况,发现苹果的日销售量y(单位:千克)关于售价x(单位:元千克)的回归方程为,则下列结论正确的是( )
A.若售价每增加1元千克,则日销售量平均减少12.5千克
B.若售价为10元千克,则日销售量一定是175千克
C.若水果店想要将店内的200千克的苹果在当日销售完,则售价预计不高于8元千克
D.若售价定为12元千克且苹果数量充足,则当日苹果销售收入约为1800元
11.已知椭圆过点,直线与椭圆C交于M,N两点,且线段的中点为P,O为坐标原点,直线的斜率为,则下列结论正确的是( )
A.C的离心率为
B.C的方程为
C.若,则
D.若,则椭圆C上存在E,F两点,使得E,F关于直线l对称
三、填空题:本题共3小题,每小题5分,共15分。
12.已知随机变量,若,则______.
13.用模型拟合一组数据时,为了求出回归方程,设,其变换后得到线性回归方程,则_____.
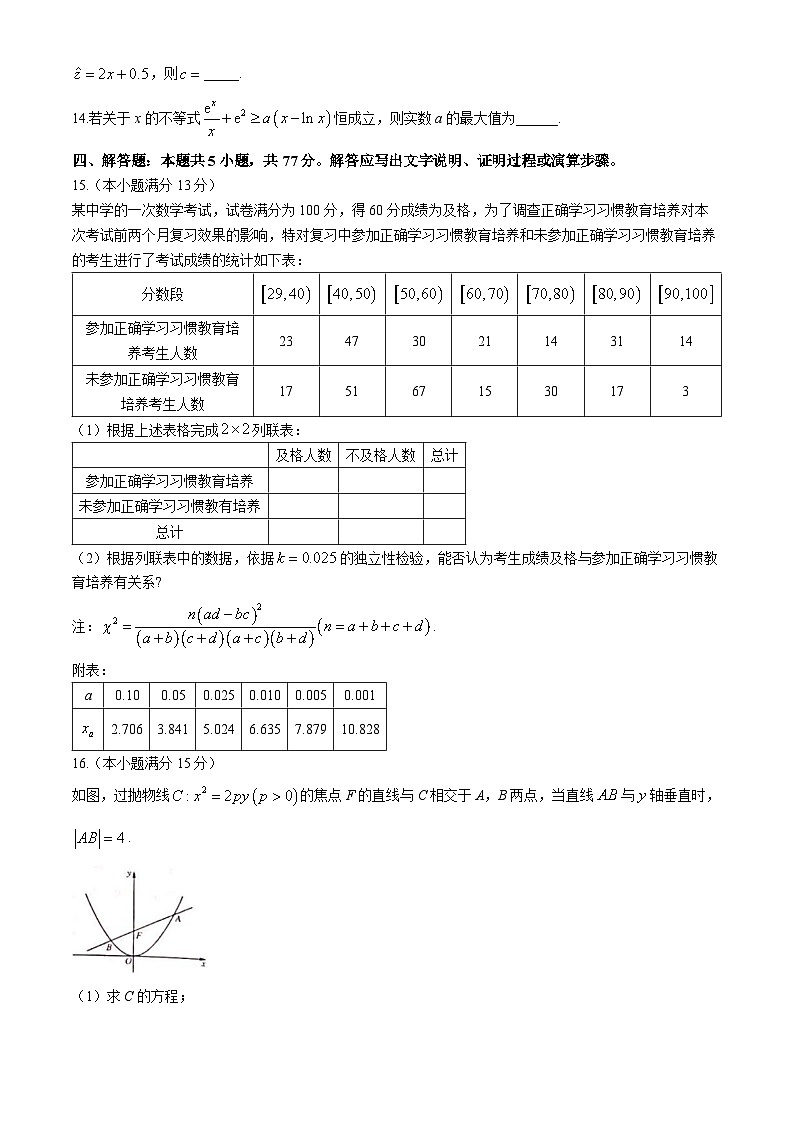
14.若关于x的不等式恒成立,则实数a的最大值为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(本小题满分13分)
某中学的一次数学考试,试卷满分为100分,得60分成绩为及格,为了调查正确学习习惯教育培养对本次考试前两个月复习效果的影响,特对复习中参加正确学习习惯教育培养和未参加正确学习习惯教育培养的考生进行了考试成绩的统计如下表:
(1)根据上述表格完成列联表:
(2)根据列联表中的数据,依据的独立性检验,能否认为考生成绩及格与参加正确学习习惯教育培养有关系?
注:.
附表:
16.(本小题满分15分)
如图,过抛物线的焦点F的直线与C相交于A,B两点,当直线与轴垂直时,.
(1)求C的方程;
(2)以为直径的圆能否经过坐标原点O?若能,求出直线的方程;若不能,请说明理由.
17.(本小题满分15分)
如图,在四棱锥中,平面底面,,,,,,.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
18.(本小题满分17分)
2023年全国竞走大奖赛(第1站)暨世锦赛及亚运会选拔赛3月4日在安徽黄山开赛.重庆队的贺相红以2小时22分55秒的成绩打破男子35公里竞走亚洲纪录.某田径协会组织开展竞走的步长和步频之间的关系的课题研究,得到相应的试验数据:
(1)根据表中数据,得到步频和步长近似为线性相关关系,求出y关于x的回归直线方程,并利用回归方程预测,当步长为时,步频约是多少?
(2)记,其中为观测值,为预测值,为对应的残差,求(1)中步长的残差的和,并探究这个结果是否对任意具有线性相关关系的两个变量都成立?若成立,请证明;若不成立,请说明理由.
参考数据:,.
参考公式:,.
19.(本小题满分17分)
已知函数.
(1)讨论的单调性;
(2)若有两个零点,求a的取值范围.
2023~2024学年高二5月质量检测卷·数学
参考答案、提示及评分细则
1.C 判断两个分类变量是否有关的最有效方法是进行独立性检验.故选C.
2.B 由已知,得,,又经过点,所以,解得.故选B.
3.D 因为,所以,因为,所以.于是,所以.故选D.
4.B 在线性回归分析中,越大拟合效果越好,越小拟合效果越差.故选B
5.A 的展开式中,含x的项是4个因式中任取1个因式选择x,另外3个因式中选择常数项相乘积的和,则的展开式中,含x的项为,所以x的系数为.故选A.
6.C 设事件表示从甲箱中随机取出一个红球,事件表示从甲箱中随机取出一个白球,事件B表示从乙箱中随机取出一个红球,则,,,,所以.故选C
7.D 先排列3幅书法作品有种排法,再将3幅美术作品插入3幅书法作品形成的3个空中,有种排法,所以不同排列方法有种.故选D.
8A 设,,由对称性不妨设点A在第一象限,此时M也在第一象限,因为,所以,,所以,又,解得,,,所以,所以,解得,所以,代入双曲线方程,得,解得,,所以.故选A.
9.BD 由图形特征可知,对应的样本数据都是负相关,所以,都是负数,又对应的样本数据比对应的样本数据的线性相关程度更强,所以,,对应的样本数据都是正相关,又对应的样本数据比对应的样本数据的线性相关程度更强,所以,所以BD正确。故选BD.
10.ACD 对于A,由知售价每增加1元千克,则日销售量平均减少12.5千克,A正确;
对于B,若售价为10元千克,则日销售量可能是175千克,B错误;
对于C,若日销售量为200千克,则,所以售价预计不高于8元千克,C正确;
对于D,若,则,,故当日苹果销售收入约为1800元,D正确.
故选ACD
11.AC 设,,则,即.
因为M,N在椭圆C上,所以,,两式相减,
得,即,
又,所以,
即,所以,离心率,故A正确;
因为椭圆C过点,所以,解得,,所以椭圆C的标准方程为,故B错误;若,则直线l的方程为,由得,所以,,,故C正确;
若,则直线l的方程为.假设椭圆C上存在E,F两点,使得E,F关于直线l对称,设,,的中点为,所以,,因为E,F关于直线l对称,所以且点Q在直线l上,即.又E,F在椭圆C上,所以,,两式相减,得,即,所以,即.联立,解得,即.又,所以点Q在椭圆C外,这与Q是弦的中点矛盾,所以椭圆C上不存在E,F两点,使得E,F关于直线l对称.
故选AC.
12.0.2 由正态分布的性质得.
13. 由,得,故,所以.
14. 不等式,即,所以.
设,则,
所以当时,,单调递减;
当时,,单调递增,所以.
令,则.
当时,,单调递增,则,故满足条件;
当时,在上单调递减,在上单调递增,则,
设,则,则在上单调递减,
又,
所以,所以,所以a的最大值为.
15.解:(1)根据题表中数据可以得到列联表如下:
(2)零假设为:考生成绩及格与参加正确学习习惯培养无关。
.
依据的独立性检验,不成立,故可以认为考生成绩及格与参加正确学习习惯培养有关系。
16.解:(1)F点的坐标是,
当直线与y轴垂直时,点A,B的坐标分别是,,
,解得,
所以C的方程是.
(2)以为直径的圆不可能经过坐标原点O,理由如下:
直线的斜率显然存在,设其方程为,
代入,消去y并整理得,
设,,则.
因为,
所以与不垂直.
因此,以为直径的圆不可能经过坐标原点.
17.(1)证明:过点D作于N,
因为,,,,
所以,,所以,,
所以,所以,
因为平面平面,平面平面,平面,
所以平面,
又平面,所以
又,,,平面,
所以平面.
(2)解:因为,,所以,
如图,以D为坐标原点,,所在直线分别为x轴,y轴,以过点D且垂直于平面的直线为z轴,建立如图所示的空间直角坐标系,
则,,,,
所以,,.
设平面的一个法向量为,则,
令,则,,所以,
设直线与平面所成角为θ,
则,
所以直线与平面所成角的正弦值为.
18.解:(1),,
,,
所以回归直线方程为,
将代入得,解得,所以当步长为时,步频约是0.27秒.
(2)根据(1)得到,;
,;
,;
,;
,,
所以,即步长残差和为0.
对任意具有线性相关关系的两个变量都成立,证明如下:
.
19.解:(1)的定义域为,
,
(i)若,则,所以在上单调递减;
(ii)若,则由得.
当时,;当时,,
所以当时,在上单调递减,在上单调递增.
(2)(i)若,由(1)知,至多有一个零点.
(ii)若,由(1)知,
当时,取得最小值,最小值为.
①当时,由于,故只有一个零点;
②当时,由于,即,故没有零点;
③当时,,即.
又,
故在上有一个零点.
设正整数满足,
则.
由于,因此在上有一个零点.
综上,a的取值范围为.模型
1
2
3
4
0.67
0.85
0.49
0.23
分数段
参加正确学习习惯教育培养考生人数
23
47
30
21
14
31
14
未参加正确学习习惯教育培养考生人数
17
51
67
15
30
17
3
及格人数
不及格人数
总计
参加正确学习习惯教育培养
未参加正确学习习惯教有培养
总计
a
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
步频x(单位:s)
0.28
0.29
0.30
0.31
0.32
步长y(单位:cm)
90
95
99
103
117
及格人数
不及格人数
总计
参加正确学习习惯教育培养
80
100
180
未参加正确学习习惯教有培养
65
135
200
总计
145
235
380
山西省部分学校2023-2024学年高三下学期开学质量检测试题 数学 Word版含解析: 这是一份山西省部分学校2023-2024学年高三下学期开学质量检测试题 数学 Word版含解析,共14页。试卷主要包含了本试卷分选择题和非选择题两部分,本卷命题范围,已知等比数列的前项和为,若,则,已知向量,,若,则,已知椭圆,下列说法正确的是等内容,欢迎下载使用。
山西省部分学校2024届高三下学期开学质量检测数学试题: 这是一份山西省部分学校2024届高三下学期开学质量检测数学试题,共14页。试卷主要包含了本试卷分选择题和非选择题两部分,本卷命题范围,已知等比数列的前项和为,若,则,已知向量,,若,则,已知椭圆,下列说法正确的是等内容,欢迎下载使用。
山西省长治市部分学校2023-2024学年高一上学期11月质量检测数学试题: 这是一份山西省长治市部分学校2023-2024学年高一上学期11月质量检测数学试题,共4页。












