高教版（2021·十四五）基础模块 下册7.2 旋转体教课内容课件ppt

这是一份高教版（2021·十四五）基础模块 下册7.2 旋转体教课内容课件ppt，共28页。PPT课件主要包含了旋转体相关概念，新知1，组合体，新知2，圆柱的结构特征，圆锥的结构特征，答案20，答案4，球的有关概念，球的性质等内容，欢迎下载使用。
一条平面曲线绕一条定直线旋转一周所形成的曲面称为旋转面，由封闭的旋转面围成的几何体称为旋转体，其中的平面曲线称为旋转体的母线，定直线称为旋转体的轴。
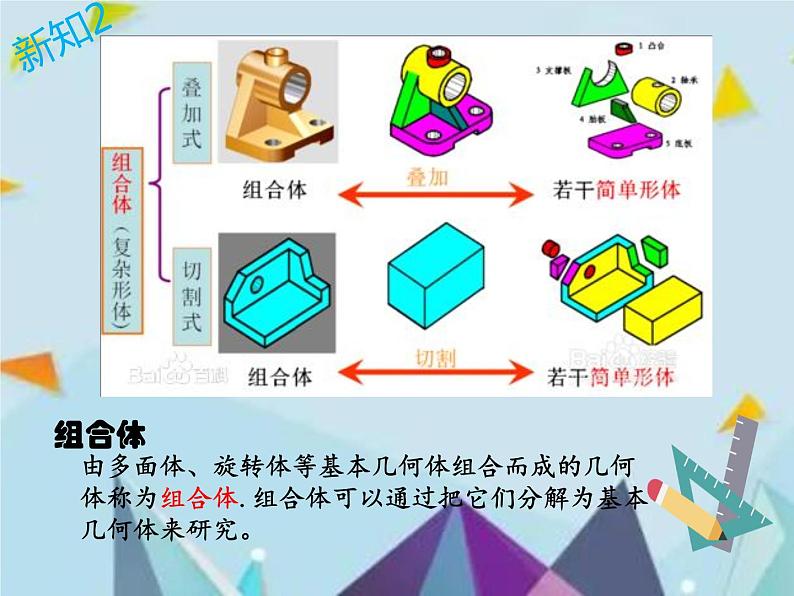
由多面体、旋转体等基本几何体组合而成的几何体称为组合体.组合体可以通过把它们分解为基本几何体来研究。
问题1：圆柱，圆锥和圆台是否可以由平面图形得到？如果可以，它们是由平面图形如何得到呢？
圆柱可以看成以矩形的一边所在直线为旋转轴，将矩形旋转一周而形成的曲面所围成的几何体；
圆锥可看成以直角三角形一直角边所在直线为旋转轴，将直角三角形旋转一周而形成的曲面所围成的几何体；
圆台可看成以直角梯形垂直于底边的腰所在直线为旋转轴，将直角梯形旋转一周而形成的曲面所围成的几何体．
问题2：任意平面多边形以一条边所在直线为旋转轴，其他边旋转一周而形成的曲面围城的几何体可以统一称为什么呢？
旋转体. 旋转轴(定直线)称为旋转体的轴； 在轴上的边（或它的长度）称为旋转体的高； 垂直于轴的边旋转而成的圆面称为旋转体的底面； 不垂直于轴的边旋转而成的曲面称为旋转体的侧面； 不垂直于轴的边都称为母线； 在旋转体中，通过轴的平面所得到的的截面通常简称为轴截面.
以矩形的一边所在直线为旋转轴,其余边旋转形成的面所围成的旋转体叫做圆柱。
圆柱的轴：旋转轴叫做圆柱的轴。
圆柱的底面：垂直于轴的边旋转而 成的圆面叫做圆柱的底面。
圆柱的侧面：平行于轴的边旋转而成的 曲面叫做圆的侧面。
圆柱侧面的母线：无论旋转到什么位置，不垂直 于轴的边都叫做圆柱侧面的母线。
圆柱用表示它的轴的字母表示.如：圆柱OO'
注：棱柱与圆柱统称为柱体
以直角三角形的一条直角边所在直线为旋转轴, 两余边旋转形成的面所围成的旋转体叫做圆锥。
轴：作为旋转轴的直角边叫做圆锥的轴。
底面：另外一条直角边旋转形成的圆 面叫做圆锥的底面。
侧面：直角三角形斜边旋转形成的曲 面叫做圆锥的侧面。
顶点：作为旋转轴的直角边与斜边 的交点
母线：无论旋转到什么位置，直角三角形 的斜边叫做圆锥的母线。
圆锥可以用它的轴来表示。如：圆锥SO
注：棱锥与圆锥统称为锥体
问题3：圆台是否可以看成平面截圆锥得到的几何体？如果可以，那么任意一个平面都可以截圆锥得到圆台吗？圆台的上下底面之间的数量关系是什么？
答：圆台可以看成平行于圆锥底面的 平面截圆锥所得到的几何体. 圆台上下底面相似．
圆台的轴，底面，侧面，母线与圆锥相似
注：棱台与圆台统称为台体。
圆柱圆锥圆台的侧面展开图是平面图形吗？如果是平面图形，那么是什么图形呢？求它们的面积需要旋转体的那么条件呢？
圆柱的侧面展开图是矩形，矩形的长是圆柱的底面周长，高是圆柱的高(即母线长)，所以圆柱的侧面积为S=2πrl
圆锥的侧面展开图为扇形，扇形半径为圆锥的母线，扇形的弧为圆锥的底面周长，所以圆锥的侧面积为S=πrl
练习（1）写出圆柱中任意两条母线的位置关系，任意一条母线 与底面的位置关系，以及两个底面的位置关系？（2）写出圆锥中任意两条母线的位置关系，任意一条母线 与底面的位置关系？（3）写出圆台中任意两条母线的位置关系，任意一条母线 与底面的位置关系？
解：由圆柱、圆锥和圆台的定义可知（1）圆柱中任意两条母线平行，母线与底面相交，两底面平行；
（2）圆锥中任意两条母线相交，任意一条母线与底面相交；
（3）圆台中任意两条母线相交，任意一条母线与底面相交.
练习分别求出底面半径为1cm,高为3cm的圆柱和圆锥的表面积.
练习一个圆锥的母线长为20，母线与轴的夹角为30º，求圆锥的高.
一个圆柱的母线长为5,底面半径为2,求圆柱轴截面的面积.
一个圆台的母线长为5,两底面直径分别为2和8,求圆台的高.
日常生活中的很多物体都可以抽象成球面，如图。（1）从数学的角度应该怎样来刻画球面？圆可以看成平面 上到定点的距离等于定长的点的集合，球面上的点是 否有类似的性质？（2）球面可以通过什么图形旋转得到？球体怎样描述？
（1）回答：球面可以看成一个半圆绕着它的直径所在的直线旋转一周所形成的曲面；球面围成的几何体，称为球.球也是一个旋转体.
（2）回答：由球面的形成过程可看出，球面可以看成空间中到一个定点的距离等于定长的点的集合.
（2）球面可以通过什么图形旋转得到？
（1）从数学的角度应该怎样来刻画球面？
以半圆的直径所在的直线为旋转轴，半圆面旋转一周形成的几何体叫做球体。
球心：半圆的圆心叫做球的球心。
半径：半圆的半径叫做球的半径。
直径：半圆的直径叫做球的直径。
球的表示：用球心字母表示。如：球O
球面可以看成空间中到定点的距离等于定长的点的集合.
当用刀去切一个球形的西瓜时，所得到的截面是什么形状？一般地，一个平面与一个球面相截，所得交线的形状是怎样的?
【性质3】 到球心距离相等的截面面积 .
【性质1】 用任意平面截球所得的截面是一个 ， 球心和截面圆心的连线 ．
【性质2】 球心到截面的距离d与球的半径R及截面的半 径r有下面关系：
球面被经过球心的平面截得的圆称为球的大圆，被不经过球心的平面截得的圆称为球的小圆.
【性质4】球的直径等于球的内接长方体的 .
练习1.已知一个球的半径为3，求这个球的表面积.
答案：4π×32 = 36π
2.判断下列命题的真假.(1) 球面上任意一点与球心的连线都是球的半径；(2) 球面上任意两点连成的线段都是球的直径；(3) 用一个平面截一个球，得到的截面是一个圆面.
教材已知A,B都是球O对应的球面上的点，过A,B两点可以做几个大圆？
答案：若AB是球的直径，可做无数个大圆； 若AB不是球的直径，可做一个大圆.
教材P81练习B 3一条直线被一个半径为5的球截得的线段长为8，求球心到直线的距离.
即球面上两点间的最短距离，是指经过这两点和球心的大圆的劣弧的长度.
大圆劣弧的圆心角为α弧度，半径为R，则弧长为L=αR