48，2024年辽宁省大连市第七十六中学中考一模演练数学试题(无答案)

这是一份48，2024年辽宁省大连市第七十六中学中考一模演练数学试题(无答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

(本试卷共23道题 满分120分 考试时间：120分钟)
考生注意：所有试题必须在答题卡指定区域内作答，在本试卷上作答无效
第一部分 选择题(共30分)
一、选择题(本题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的)
1.已知一组数据如下：12，15，19，8，6，10，则这组数据的中位数为( )
A. B.13.5 C.11 D.9
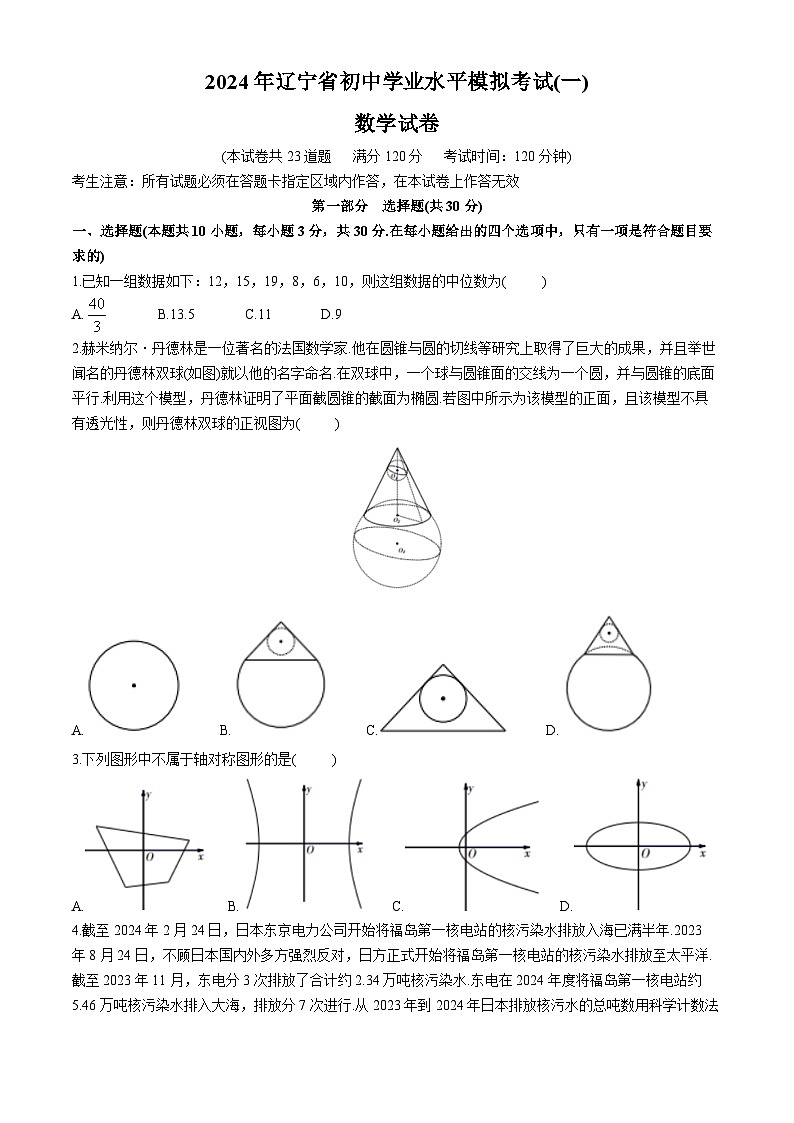
2.赫米纳尔·丹德林是一位著名的法国数学家.他在圆锥与圆的切线等研究上取得了巨大的成果，并且举世闻名的丹德林双球(如图)就以他的名字命名.在双球中，一个球与圆锥面的交线为一个圆，并与圆锥的底面平行.利用这个模型，丹德林证明了平面截圆锥的截面为椭圆.若图中所示为该模型的正面，且该模型不具有透光性，则丹德林双球的正视图为( )
A. B. C. D.
3.下列图形中不属于轴对称图形的是( )
A. B. C. D.
4.截至2024年2月24日，日本东京电力公司开始将福岛第一核电站的核污染水排放入海已满半年.2023年8月24日，不顾日本国内外多方强烈反对，日方正式开始将福岛第一核电站的核污染水排放至太平洋.截至2023年11月，东电分3次排放了合计约2.34万吨核污染水.东电在2024年度将福岛第一核电站约5.46万吨核污染水排入大海，排放分7次进行.从2023年到2024年日本排放核污水的总吨数用科学计数法该试卷源自 每日更新，提供24小时找卷服务，全网性价比高。 表示为( )
×104 B.7.8×104 C.7.5×104 ×105
5.在平面直角坐标系中，抛物线与直线交于A、B两点，点A在点B的右侧，则的值为( )
A. B.-3 C.-1 D.
6.如图，在⊙O中，OA、OB、OC为半径，连接AB、BC、AC.若∠ACB=53°，∠CAB=17°，则∠OAC的度数为( )
A.10° B.15° C.20° D.25°
7.已知一次函数，当时，，则k的值为( )
A. B. C.或 D.
8.在玩一类卡牌游戏时，作为游戏中“法官”的小胖将卡片平均分给其他参与游戏的同学(小胖作为法官不持有卡牌)，每轮每人分发一张卡牌.在分发了2轮之后，小胖发现，手中原来的x张卡牌现在仅剩3张，而参与游戏的总人数为y人，则可列方程为( )
A. B. C. D.
9.已知某扇形弧长为3π，圆心角为60°，则扇形面积为( )
A. B. C. D.
10.如图，在△ABC中，以A、B为圆心，AC、BC长为半径分别作弧交于点C'，连接BC'、AC'，在C'B上截取点M，以点C'为圆心，C'M长为半径作弧交C'C于点N，以大于MN的长分别以点M、N为圆心作弧交于一点，点C'与这点连线的直线交BC于点P，交AB于I.若BC=，CC'=4，则BP的长为( )
A. B. C. D.10
二、填空题(本题共5小题，每小题3分，共15分)
11.=__________；
12.已知在平面直角坐标系中存在点A(9，2)，将点A向右平移2个单位后，以原点O为旋转中心逆时针旋转90°后得到点A'，则A'的坐标为__________；
13.某考试院在命制试卷时，命制了A、B、C三套卷，且三套卷难度相当.公平起见，考试院决定在三套卷中随机抽取2套分别下发给甲、乙两地使用，每套卷子被抽到的概率相同，则抽到A、C卷的概率为__________；
14.如图，在平面直角坐标系中，双曲线上有一动点A，连接OA并延长至点B，使得OA=OB，点C在x轴上，连接BC交双曲线于点D，延长AD交x轴于点E.若∠ADC=∠OCD，OC=5，tan∠DEC=，则k的值为__________；
15.如图，在边长为2的正方形ABCD中，点E在正方形内部且∠CED=90°.连接BE，以BE、DE为边构造□BEDF，连接CF，则线段CF的最小值为__________.
三、解答题(本题共8小题，共75分.解答应写出文字说明、演算步骤或推理过程)
16.(本小题8分)
计算：(其中x≠0、1或-1)；
17.(本小题8分)
如图①、②所示，A品种小麦的试验田是边长为xm(x＞1)的正方形去掉一个边长为1m的正方形蓄水池后余下的部分，B品种小麦的试验田是边长为(x-1)m的正方形，两块试验田的小麦都收获了500kg.
(1)哪种小麦的单位面积产量高?
(2)高的单位面积产量是低的单位面积产量的多少倍?
18.(本小题9分)
【问题提出】
在一次课外活动中，小明为了探究人类记忆曲线的变化情况，决定通过让小组成员背单词的方法进行研究分析.
【收集数据】小明让小组的8位同学在一天内背诵6个单词.为了确保实验的准确性，小明没有让同学们在课余时间对单词进行复习.第2天课下，小明对单词记忆情况进行了调查，绘制统计图如下(如图1，其中横轴代表小组人员编号，纵轴代表记忆单词数量)；
【分析数据】
(1)小明统计小组成员单词记忆情况的方式为_________(选填“普查”“抽样检测”或“假设分析”)；
(2)小组成员记忆单词数量的极差为____________；
(3)求小组成员记忆单词数量的平均数和方差；
(4)若学校有1000人，估计在此调查中第二天单词记忆量高于4个的人数；
【统计总结】
小明连续收集了7天同学们对于第一天单词的记忆数量，经过统计后，取合适的自变量和因变量在坐标系中通过描点连线的方法绘制图象如下图(图中横轴代表天数，纵轴代表遗忘速度)：
(5)根据小明绘制的图象简图，请你对于记忆单词给出一点建议(要求：结合函数图象，且不多于50字)
__________________________________________________________________________________.
19.(本小题8分)
某网络公司给出了下列三种上宽带网的收费方式(如下表)
根据表格回答：
(1)请写出A、B、C上网时间t(单位：h)关于总费用y(单位：元)的函数解析式；
(2)试探究选取哪种方式能够节省上网费用，并说明理由.
20.(本小题8分)
如图，在⊙O中，四边形ABCD内接于⊙O，连接BD，∠ABC=90°，点E在AD延长线上，且∠E=∠ABD.
(1)探究CE与⊙O的位置关系，并证明；
(2)连接OE，若tan∠ABD=，AD=3，求OE的长.
21.(本小题8分)
如图1，大连大黑山被誉为辽南第一山的大黑山.大黑山拔海而起，滨岸而立，怪石嶙峋，气势壮观.如图2，假设有一航线l经过大黑山景区且与地面平行，现有一架客机沿航线l飞经景区上空，机上有一乘客使用测距相机进行拍照.当飞机恰好飞经主峰峰顶A时，该乘客自上而下正对主峰进行拍照，测得客机到主峰A的距离AB为300m，山谷谷底C到客机B的仰角为60°.
(1)求点A到直线BC的距离；
(2)飞机又以250m/s的速度向右飞行了1.6s到达点D.此时乘客测得点E关于客机的仰角为83°，∠ADE=60°，DE=400m.根据以上信息和参考数据，求主峰A和次峰E之间的距离.
(结果保留根号，参考数据：sin37°≈0.6，cs37°≈0.8)
22.(本小题12分)
如图，在平面直角坐标系中，抛物线C：两条切线的函数解析式分别为：，：.
(1)求抛物线的解析式；
(2)抛物线C与x轴的两个交点分别为A、B，切线l1切抛物线于点C，、交于点D.
①求sin∠ADC的值；
②点E为抛物线C上一动点，过E分别作、的平行线分别交抛物线C于G、F，连接FG.点H为FG的中点.求证：点H的纵坐标为定值.
23.(本小题12分)
综合与实践
问题情境：数学课上，于老师出示了一个问题：
“如图，在Rt△ABC中，∠A=90°，过B作BD⊥BC，连接CD.直线CD经过AB的中点E.在BA上截取点F，使BF=AC，过F作FH⊥CD交BC于点H，垂足为G，连接BG.请直接写出图中与∠ACB相等的角.”
独立思考：(1)请解答于老师提出的问题.
实践探究：(2)在原有条件不变的情况下，于老师提出了新问题，请你解答.
“∠BGH的度数是否为定值?若为定值，请求出∠BGH的度数；若不是定值，请求出∠BGH的度数变化范围.”
问题解决：(3)数学活动小组的同学对上述问题进行特殊化研究之后发现，保留原题条件，如果给出图中任意两条线段的长度，则图中所有已经用字母标记的任意线段的长度均可求.该小组提出下面的问题，请你解答.
“在原题的条件下，若AC=6，AB=8，求BG的长.”
收费方式
月使用费/元
包时上网时间/h
超时费/(元/min)
A
30
25
0.05
B
50
50
0.05
C
120