广西壮族自治区来宾市2023-2024学年八年级下学期4月期中考试数学试题（原卷版+解析版）

这是一份广西壮族自治区来宾市2023-2024学年八年级下学期4月期中考试数学试题（原卷版+解析版），文件包含广西壮族自治区来宾市2023-2024学年八年级下学期4月期中考试数学试题原卷版docx、广西壮族自治区来宾市2023-2024学年八年级下学期4月期中考试数学试题解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
注意事项：
1．满分120分，答题时间为120分钟．
2．请将各题答案填写在答题卡上．
一、单项选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的）
1. 下列图标中，是中心对称图形的是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】本题考查了中心对称，掌握中心对称的概念是解题的关键．若把一个图形绕某点旋转，旋转后的图形能和原图形重合，则这个图形为中心对称图形．
【详解】解：根据中心对称的概念可得B选项是中心对称图形，
故选：B．
2. 在中，，则的长为（ ）
A. B. C. 4D. 5
【答案】D
【解析】
【分析】如图所示，直接根据勾股定理即可得出答案．
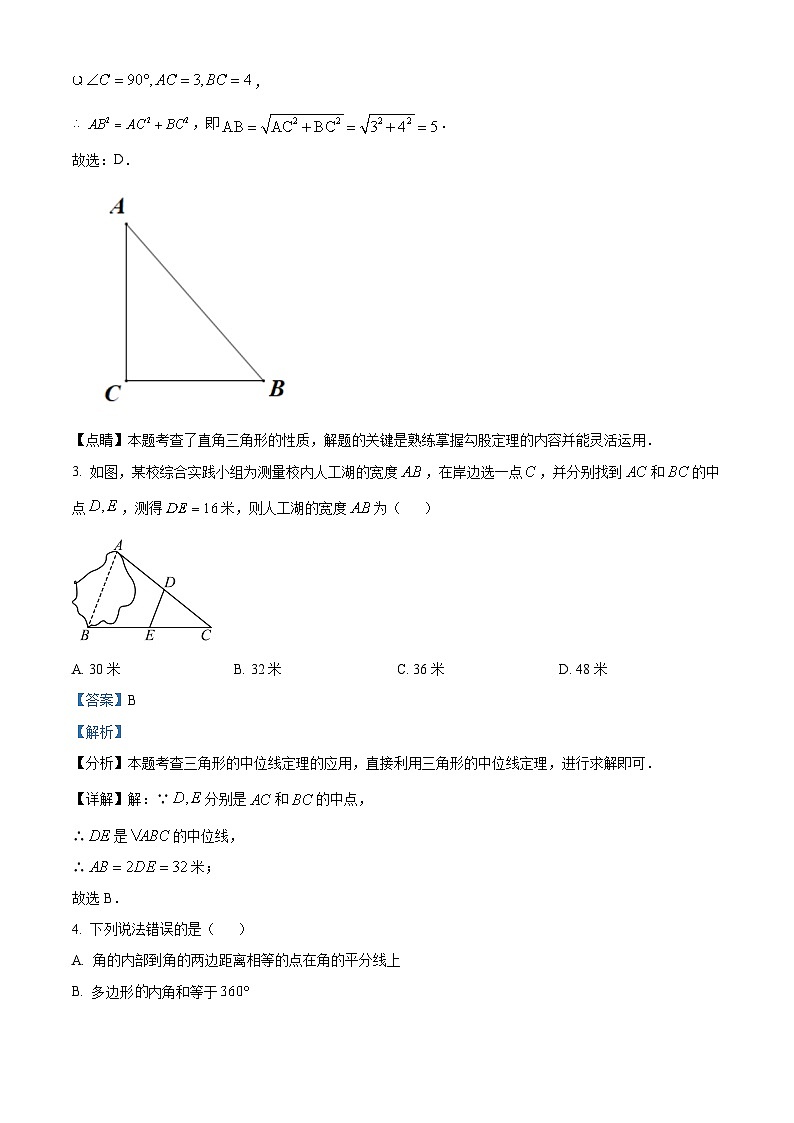
【详解】如图所示，
，
，即．
故选：D．
【点睛】本题考查了直角三角形的性质，解题的关键是熟练掌握勾股定理的内容并能灵活运用．
3. 如图，某校综合实践小组为测量校内人工湖的宽度，在岸边选一点，并分别找到和的中点，测得米，则人工湖的宽度为（ ）
A. 30米B. 32米C. 36米D. 48米
【答案】B
【解析】
【分析】本题考查三角形的中位线定理的应用，直接利用三角形的中位线定理，进行求解即可．
【详解】解：∵分别是和的中点，
∴是的中位线，
∴米；
故选B．
4. 下列说法错误的是（ ）
A. 角的内部到角的两边距离相等的点在角的平分线上
B. 多边形内角和等于
C. 直角三角形的两锐角互余
D. 全等三角形的对应角相等
【答案】B
【解析】
【分析】本题考查了角平分线的性质，直角三角形的性质，全等三角形的性质和多边形的内角和，掌握相关的知识是解题的关键．根据角平分线的性质，直角三角形的性质，全等三角形的性质和多边形的内角和逐一判断即可．
【详解】解：A、角的内部到角的两边距离相等的点在角的平分线上，该选项正确，不符合题意；
B、多边形的内角和为，该选项错误，符合题意；
C、直角三角形的两锐角互余，该选项正确，不符合题意；
D、全等三角形的对应角相等，该选项正确，不符合题意；
故选：B．
5. 下列各组数是勾股数是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题考查勾股数，根据勾股数是满足的三个正整数逐项判断即可．
【详解】解：A、∵，∴不是勾股数，不符合题意；
B、∵，∴不是勾股数，不符合题意；
C、∵都不是整数，∴不是勾股数，不符合题意；
D、∵，∴是勾股数，符合题意；
故选：D．
6. 如图，在平行四边形中，，则（ ）
A. B. C. D.
【答案】D
【解析】
【分析】此题考查了平行四边形的性质：对角相等，邻角互补，根据平行四边形的性质得到，，即可求出答案．
【详解】解：∵四边形是平行四边形，
∴，，
∵
∴，
∴，
故选：D．
7. 如图，，点在直线上，点在直线上，，，若，则的度数为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查等边对等角，平行线的性质，根据等边对等角，得到，根据两直线平行，内错角相等，得到，即可得出结果．
【详解】解：∵，，
∴，
∵，
∴；
故选C．
8. 如图，在中，，平分，，，则（ ）

A. 4B. 3C. 2D. 1
【答案】D
【解析】
【分析】过D点作，垂足为E，由已知，，可求，再利用角平分线性质证明即可，熟练掌握角平分线的性质是解题关键．
【详解】解：过D点作，垂足为E，

∵
∴，
∵，
解得，
∵平分，，，
∴．
故选D．
9. 在中，所对的边分别是，且，则下列等式正确的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】本题主要考查了直角三角形的性质．设，根据三角形内角和定理可得是直角三角形，且c是斜边，从而得到，，即可求解．
【详解】解：设，
∴，
解得：，
∴，
∴是直角三角形，且c是斜边，
∴，，
故选项A，B，C错误，选项D正确．
故选：D
10. 某校在消防主题公园周边修了3条小路，如图，小路恰好互相垂直，小路的中点刚好在湖与小路的相交处．若测得的长为，的长为，则的长为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题考查了勾股定理以及斜边上的中线等于斜边的一半，先根据勾股定理算出，再结合斜边上的中线等于斜边的一半，得出，即可作答．
【详解】解：小路恰好互相垂直，
∴，
∵点是小路的中点，
∴，
故选：A．
11. 如图，四边形的对角线，相交于点O，，且，则添加下列一个条件能判定四边形是菱形的是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据菱形的判定方法分别对各个选项进行判定，即可得出结论．
【详解】解：∵，
∴，
∵，
∴，
∴，
∴四边形是平行四边形，
当时，四边形是矩形；故选项A不符合题意；
∵，
∴，
∴，
∴，
∴四边形为菱形，故选项B符合题意；
∵，
∴，
∵，
∴，
∴四边形是矩形；故选项C不符合题意；
当时，不能判定四边形为菱形；故选项D不符合题意．
故选：B．
【点睛】本题考查了菱形的判定，平行四边形的判定和性质，等腰三角形的判定和性质，熟练掌握菱形的判定定理是解题的关键．
12. 如图，在矩形中，边上分别有两个动点，连接，若，，则四边形的周长的最小值是（ ）
A. 23B. 16C. 22D. 15
【答案】B
【解析】
【分析】本题考查矩形的判定和性质，全等三角形的判定和性质，勾股定理，延长到点，使得，连接，易得四边形和四边形是矩形，证明，得到，进而得到当三点共线时，的值最小，勾股定理求出的长，进一步求出四边形的周长的最小值即可．
【详解】解：如图，延长到点，使得，连接．
，四边形是矩形，
∴，
四边形和四边形是矩形．
∴，，
，
，
，
．
分别是上的动点，故当三点共线时，的值最小，
且的值等于的值．
在中，，
四边形的周长的最小值是．
二、填空题（本大题共6小题，每小题2分，共12分）
13. 正六边形的每个内角等于______________°．
【答案】120
【解析】
【详解】解：六边形的内角和为：（6-2）×180°=720°，
∴正六边形的每个内角为：，
故答案为：120
14. 若直角三角形的两条直角边长分别为，则第三条边长的值是______．
【答案】3
【解析】
【分析】本题考查勾股定理，实数的运算，根据勾股定理进行求解即可．
【详解】解：由勾股定理，得：，
∴（负值舍去）；
故答案为：3．
15. 如图，平行四边形的对角线与相交于点，，若，，则长为____．
【答案】10
【解析】
【分析】本题考查了平行四边形的性质以及勾股定理的运用，利用平行四边形的性质和勾股定理求的长，进而可求出的长．
【详解】∵平行四边形的的对角线与相交于点，
，，
，，
，
，
故答案为：10．
16. 如图，在矩形中，对角线相交于点．若，，则的长为______．
【答案】
【解析】
【分析】本题主要考查了矩形的性质，勾股定理，等边三角形的性质与判定，先由矩形的性质得到，，证明是等边三角形，得到，利用勾股定理求解即可．
【详解】解：∵四边形是矩形，
∴，，
∵，
∴是等边三角形，
∴，
∴，
故答案为：．
17. 若一个直角三角形的周长为56，斜边长为25，则该直角三角形的面积为______．
【答案】84
【解析】
【分析】本题考查勾股定理，完全平方公式，根据题意，得到，利用完全平方公式，求出的值即可得出结果．
【详解】解：设两条直角边为，
由题意，得：，
∴，
∴，
∴该直角三角形的面积为；
故答案为：84．
18. 如图，在Rt中，，，，是边上的一个动点，于点，于点，则的最小值为______．
【答案】
【解析】
【分析】本题考查矩形的判定和性质，垂线段最短，勾股定理，连接，证明四边形为矩形，得到，根据垂线段最短，得到时，最小，即最小，等积法求出的长即可．
【详解】解：连接，
∵，，，
∴，
∵于点，于点，，
∴四边形为矩形，
∴，
∴当最小时，最小，
∴当时，最小，即最小，
此时，即：，
∴；
∴的最小值为；
故答案为：．
三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤）
19. 如图所示，是的中线，，，垂足分别为F，E，．求证：．

【答案】见解析
【解析】
【分析】本题考查了全等三角形的判定定理--，熟记定理内容是解题关键．
【详解】证明：∵是的中线，
∴
∵，，
∴
∵
∴
20. 如图，小肖同学从滑雪台处开始向下滑至处．已知滑雪台的高度为14米，滑雪台整体的水平距离比滑雪台的长度短2米，则滑雪台的长度为多少米？
【答案】滑雪台的长度为50米
【解析】
【分析】本题考查勾股定理，设的长为米，则的长为米，利用勾股定理进行求解即可．
【详解】解：设的长为米．则的长为米．
米，是直角三角形，，
，
，解得．
答：滑雪台的长度为50米．
21. 如图，在中，是边上的一点，且，若，，求证：是直角三角形．
【答案】见解析
【解析】
【分析】本题考查中垂线的判定和性质，勾股定理逆定理，连接，易得：，进而得到，进而推出，得到，即可得出结论．
【详解】证明：如图，连接．
，，
．
，
．
，
，
是直角三角形，，
是直角三角形．
22. 如图，在矩形中，相交于点，过点分别作，，连接．
（1）求证：四边形是菱形．
（2）若，，求的长．
【答案】（1）见解析 （2）
【解析】
【分析】本题考查矩形的性质，菱形的判定，等边三角形的判定和性质，含30度角的直角三角形的性质，勾股定理等知识点，熟练掌握相关知识点，是解题的关键．
（1）先证明四边形是平行四边形，根据矩形的性质和一组邻边相等的平行四边形是菱形，证明即可；
（2）菱形的性质，求出的长，证明是等边三角形，求出的值，再利用勾股定理尽心求解即可．
【小问1详解】
证明：，，
，，
四边形是平行四边形．
四边形是矩形，
，
四边形是菱形．
【小问2详解】
，且四边形菱形，
，
．
，，
是等边三角形，
．
在中，，，
．
23. 如图，四边形是平行四边形，对角线与相交于点，且平分．
（1）请用无刻度的直尺和圆规过点作，交的延长线于点．（保留作图痕迹，不写作法）．
（2）在（1）的条件下，若，求的面积．
【答案】（1）见解析 （2）
【解析】
【分析】（1）根据尺规作图作一个，即可；
（2）先证明四边形是菱形，勾股定理求出的长，进而求出的长，证明四边形为平行四边形，得到，再用面积公式进行求解即可．
【小问1详解】
解：作图如图所示．
【小问2详解】
四边形是平行四边形，
，
．
平分，
，
，
，
四边形是菱形，
，
，
，．
，，
四边形是平行四边形，
．
，
．
【点睛】本题考查菱形的判定和性质，平行四边形的判定和性质，勾股定理，尺规作一个角等于已知角，熟练掌握相关知识点，是解题的关键．
24. 如图，在菱形中，若，，过点作于点．
（1）菱形的面积为 ．
（2）求的长．
（3）过点作，垂足为，求四边形的面积．
【答案】（1）24 （2）
（3）
【解析】
【分析】本题考查菱形的性质，勾股定理，矩形的判定和性质：
（1）利用面积公式进行求解即可；
（2）等积法求出的长即可；
（3）根据题意，画出图形，得到四边形为矩形，利用矩形的面积公式进行求解即可．
小问1详解】
解：∵菱形，，，
∴菱形的面积为；
故答案为：24；
【小问2详解】
∵菱形，，，
∴，
∴，
∵，
∴菱形的面积，
∴；
【小问3详解】
∵，，
∴，
∵，
∴四边形为矩形，
∴四边形的面积．
25. 小林同学是一名剪纸爱好者，喜欢运用数学知识对自己的剪纸作品进行分析思考，下面是他利用勾股定理对部分剪纸作品的数量关系进行探究思考的过程，请你帮助他一起完成．

（1）如图1，图案1是以Rt的三条边为直径，向外作半圆，其面积分别记为，请写出之间的数量关系： ．
（2）如图2，这是由四个全等的直角三角形紧密地拼接形成的飞镖状图案，测得外围轮廓（实线）的周长为80，，求该飞镖状图案的面积．
（3）如图3，这是由八个全等的直角三角形紧密地拼接形成的大正方形，记图中正方形，正方形，正方形的面积分别为．若，则 ．
【答案】（1）
（2）
（3）
【解析】
【分析】本题考查勾股定理，以直角三角形的三边构成的图形的面积问题：
（1）利用圆面积公式，结合勾股定理进行求解即可；
（2）根据周长公式和勾股定理求出的长，分割法求出面积即可；
（3）利用勾股定理结合正方形的面积公式以及面积关系，求解即可．
【小问1详解】
解：由题意，得：，，
∴；
【小问2详解】
设：，由题意，得：，
∴，，
∴，
∴，
解得：，
∴飞镖状图案的面积为；
【小问3详解】
设直角三角形的长直角边为，短直角边为，斜边长为，则：，
由题意，得：，
∴
，
∴，
∴．
故答案为：．
26. 李老师善于通过合适的主题整合教学内容，帮助同学们用整体的，联系的，发展的眼光看问题，形成科学的思维习惯．下面是李老师在“矩形的折叠”主题下设计的问题，请你解答．
如图，将矩形纸片折叠，折痕分别交于点，点的对应点为，点的对应点为．
（1）观察发现
如图1，若点与点重合，则四边形的形状为 ．
（2）探究迁移
如图2，，连接，，，求的值．
（3）拓展应用
若，，点的对应点落在边上，求线段的长的取值范围．
【答案】（1）菱形 （2）
（3）
【解析】
【分析】（1）根据折叠的性质得到，然后根据平行线的性质得到，进而得到，可以得到，即可得到结论；
（2）由矩形的性质，利用勾股定理求出和的长，然后求比值即可；
（3）借助图形得到点落在边上的情况，利用勾股定理求出长即可解题．
【小问1详解】
解：由翻折可得：，
又∵是矩形，
∴，
∴，
∴，
∴，
∴四边形是菱形，
故答案为：菱形；
【小问2详解】
解：∵，，
∴，
由折叠可得，，
∴，
过点E作于点G，则和是矩形，
∴，，
∴，
∴；
【小问3详解】
如图，当点沿折叠落在上时，
则，
∴，
∴，
又∵，，
∴是正方形，
∴，
当点C落到点A时，如图1，
设，则，
在中，，即，
解得：，
∵点的对应点落在边上，
∴线段的长的取值范围为．
【点睛】本题考查矩形与折叠，菱形的判定，勾股定理，掌握矩形的判定和性质是解题的关键．